一、SVM要解决的问题
1、什么样的决策边界才是最好的?
2、特征数据本身就很难分,怎么办?
3、计算复杂度怎么样,能应用到实际中吗?
二、最大间隔分类器
最大间隔原则:最大化两个类最近点之间的距离
–这个距离被称为间隔
–边缘上的点被称为支持向量
我们先假设分类器是线性可分的,那么有:

如图间隔就是蓝色实线和黑色虚线以及橙色虚线的距离,支持向量就是位于黑色虚线以及橙色虚线上的点。支持向量机要做的就是去找到一条线使得间隔最大,在多维空间上就是找到一个超平面。
三、硬间隔SVM
1、定义标签
首先我们有数据集:(x1,y1),(x2,y2)… (xn,yn)
y的样本类别:当x为正例时 y = +1 ,当x为负例时y = -1
决策方程:
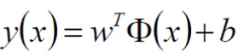
那么有: y(xi) > 0 <=> yi = +1
y(xi) < 0 <=> yi = -1
所以:yi*y(xi) > 0
2、距离的计算(方便后文理解)
在样本空间中,划分超平面可以通过如下线性方程描述:
![]()
样本 空间中任意点x到超平面的距离可写为:
![]()
3、优化的目的
通俗解释:找到一条线(w和b),使得离这条线最近的点(雷区)能够最远
将点到直线的距离化简得:

因为
yi*y(xi)>0
,所以可以直接去绝对值)
4、目标函数
目标,找到距离分割超平面最近的样本,让它距离分割超平面距离最大(泛化性能最好)
那么我们的目标函数为:

将1/||w||提到前面:

这个公式看起来确实复杂,那么接下来我们对其进行等比缩放,我们对w进行等比缩放,使得它正负类别的函数值都满足|y| >= 1,也就是:(在这里解释一下何为等比缩放:2x + 2y = 2 <==> 4x + 4y =4 )
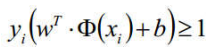
那么我们原来公式的
![]()
取最小值就是1,接下来公式就变化为:
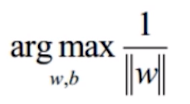
我们总结上述所有,公式加上约束条件:

一般我们不便于求最大值,所以我们将求最大目标函数改为求最小目标函数:

接下来就是求解了。
5、拉格朗日乘子法
首先简单介绍下此方法:
拉格朗日乘子法就是当我们的优化函数存在等值约束的情况下的一种最优化求解方式;其中参数α 被称为
拉格朗日乘子
,要求α不等于0



约束条件和原式:


注:其中α及时圆和曲线的交点到圆心的距离,∑aihi(x)为圆的函数,s.t表示受约束条件。
好了现在我们回到刚才的问题,那么我们的公式可以进一步转化为:

因为
![]()
所以要把左边移到右边就可以得到上式。
然后由于对偶性质,分别对w和b求偏导:


我们将其带入到公式中得到:

此时我们已经求解了
minL(w,b,a):
![]()
继续求解前面的最大值:

整理目标函数,添加负号:

经过计算可得:

求得分离超平面为:
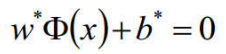
分类函数为:

四、案例
给定三个数据点:正例点x1=(3,3),x2=(4,3), 负例点x3=(1,1),构造此时的约束优化条件


将约束带入目标函数,进行化简计算:α1 + α2 = α3
带入目标函数,得到关于α1,α2的函数:

对α1,α2求偏导为0,可得到s(α1,α2)在点(1.5,-1)处取极值。而该点坐标不满足大于0的条
件,所以最小值在边界上得到。
当α1=0时,最小值s(0,2/13)=-2/13=-0.1538
当α2=0时,最小值s(1/4,0)=-1/4=-0.25
于是,s(α1, α2)在α1=1/4, α2=0时达到最小,此时α3
= α1 + α2 = 1/4
α1 = α3 = 1/4
对应的点
x1,x3
,
是支持向量
带入公式:

所以,分割超平面为:
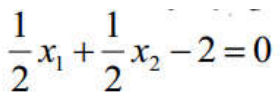
分类函数为:

五、软间隔SVM

如图所示,我们可以看出虚线的分割效果实际上是优于实线的,但是我们如果用硬间隔SVM来进行划分往往会得到实线的效果,这是因为硬间隔SVM容易受到离群点的影响,所以接下来我们需要引入
松弛因子
来优化。
引入松弛因子后原式变为:
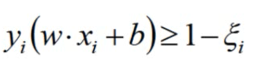
目标函数变为:

其中C是我们自己定义的
C的值越大:越严格不能有错误
C的值越小:允许误差的范围越大

六、核函数
1、问题引出
前面我们假设数据是线性可分的,也就是说存在一个超平面可以将训练样本正确分类,但是在实际任务中,原始样本空间可能不存在一个超平面能将原始训练数据正确划分,对于这类问题我们可以将原始空间的维度映射到更高的维度空间,使得在这个空间数据线性可分。
2、解决办法
我们可以使用核函数,将原有的空间映射到更高维的空间,从而可以将线性不可分问题处理到在核空间 中可分的状态
3、核函数种类

一般情况下,都使用高斯核函数进行处理操作
正常情况下需要使用网格搜索进行处理得到最优的核函数
核函数可替换:
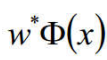
4、sklearn中的用法

注:
1、对于probability一般采用False因为我们SVM推导中并未使用到概率估计,避免带来不必要的误差。
2、degree对应的是多项式核;gamma对应的是高斯核(默认);codf0对饮Sigmoid核
5、支持向量回归(SVR)

如图以红线为中心,构造一个宽为2ε的隔离带,我们认为在隔离带里面的是可以容忍的误差,即预测正确。
用法和分类类似。
七、总结
SVM的优点:
–在高维空间中行之有效
–在决策函数中只使用训练点的一个子集(支持向量),大大节省了内存开销
–决策函教可使用不同的核函数
劣势:
–SVM不直接提供概率估计