一、引言
可恶,昨天写的长篇大论忘记保存草稿了。算了,不写原理那些东西了,直接上代码,解释几个细节。
二、代码
class Solution {
// 链式前向星必备:边结构、头数组、边数组
class Edge {
int to;
int next;
}
private int[] head;
private Edge[] edges;
private int clk = 1; // 访问顺序,全局唯一
private int[] dfn;
private int[] low;
private List<Integer> cutPoints = new ArrayList<Integer>();
/*
* 算法入口,主要是处理一下传入的边,以及对所有节点进行DFS
*
* @param n 节点的数量 edgesList 边列表,包含了一条边的正向和反向
*
* @return 割点列表
*/
public List<Integer> tarjan(int n, List<int[]> edgesList) {
if (edgesList.size() == 0)
return cutPoints;
int m = edgesList.size();
dfn = new int[n + 1];
low = new int[n + 1];
head = new int[n + 1];
edges = new Edge[m + 1];
int k = 1;
for (int[] tmp : edgesList) {
int from = tmp[0];
int to = tmp[1];
// 我的edgesList里面包含了一条边的正向和反向,因为我在外部主类中预先处理过了
// 所以这里创建链式前向星的边时,不需要正向创一条,反向创一条
edges[k] = new Edge();
edges[k].to = to;
edges[k].next = head[from];
head[from] = k++;
}
// 这个图可能是非连通的,因此要从每一个未走过的节点开始DFS,但是上一轮走过的节点不会在下一轮走到
for (int i = 1; i <= n; i++) {
if (dfn[i] == 0) {
dfs(i, i, 0);
}
}
return cutPoints;
}
void dfs(int root, int x, int father) {
low[x] = dfn[x] = clk++;
int child = 0;
int next = head[x];
boolean isCut = false;
while (next != 0) {
int to = edges[next].to;
if (dfn[to] == 0) {
child++; // 细节(1)
dfs(root, to, x);
low[x] = Math.min(low[x], low[to]);
if ((root == x && child >= 2) || (root != x && low[to] >= dfn[x]))
isCut = true;
} else if (to != father && dfn[to] < dfn[x]) { // 细节(2)
low[x] = Math.min(low[x], dfn[to]); // 细节(3)
}
next = edges[next].next;
}
if (isCut) // 细节(4)
cutPoints.add(x);
}
}
三、细节解释
下面每个标号对应代码注释中的细节标号
(1)这个细节的重点是,child++的位置,应该放在if(dfn[to] == 0) { } 这个代码块里。
首先,判断一个节点是不是割点有两种情况。
情况一,
如果节点u是根节点,且它有至少两个不通过本节点连通的子节点(不知道为什么有人说找子树,树不是没有环的吗?这里的子节点应该理解为DFS路径上,后到的节点为前到的节点的子节点),则它是一个割点
。这里理解为,如果本节点是大哥,两个子节点是小弟,如果两个小弟之间绕过大哥勾结在一起,那么大哥被干掉了,他们还是好兄弟。如果两个小弟没有私下勾结,那么大哥被干掉了,他们就分道扬镳了。
情况二,
如果节点u不是根节点,而它的子节点中至少有一个节点v的low[v]>=dfn[u],则它是一个割点
。这里理解为,如果本节点是大哥手下的一个小队长,这个小队长下面又有很多小弟,但是小弟不能越过小队长去联系大哥。如果小队长被干掉了,小弟们就找不到大哥了。
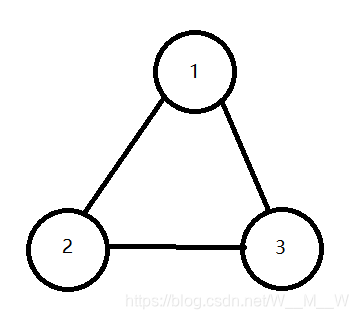
对于第一种情况,我们就是要计算一个节点的不通过本节点连通的子节点数,为什么child++一定要放在那个位置呢?看下图。如果从1开始走,依次走过1、2、3,则dfn[1]、dfn[2]、dfn[3]分别为1、2、3。回溯到节点1后,它尝试走3,发现3已经走过了,说明在本轮DFS中,1通过别的子节点到达过这个子节点,也就是这个子节点和1的至少另一个子节点是不通过本节点连通的。这里不用担心dfn[i] != 0是因为上一轮走过,因为在一轮DFS中,必然会把一个连通分量的所有点走完,也就是如果dfn[i] != 0是上一轮导致的,那么这一轮一定不会有一个节点会访问i。
只有当dfn[i] == 0的时候,说明找到了和别的子节点不连通的一个子节点。这时候如果把当前节点割掉,那么那些不通过当前节点连通的子节点就分开了。
(2)细节二
看了很多人的博客和代码,这个地方是最让我疑惑的。很多人都这么写,一个是to != father,另一个是dfn[to] < dfn[x]。
关于to != father,其实这一句不加也可以。很多人都说返祖边指向的节点不可以是父节点,但是我思来想去,觉得是可以的。我觉得这个to != father的作用不在于返祖边不可以指向父节点,而在于优化!也就是如果返祖边指向的是父节点,就根本不需要作low[x] = Math.min(low[x], dfn[to])这一步了,而一个 if(to != father) 的花费时间肯定比 low[x] = Math.min(low[x], dfn[to]) 要少,所以就加上了它。不知道这么理解有没有问题,欢迎指正。
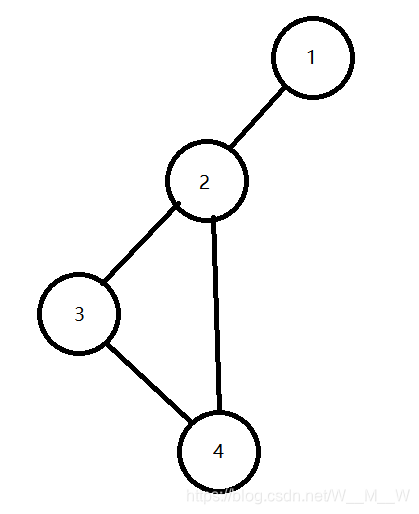
关于dfn[to] < dfn[x],其实这一句也是不加也可以。它的作用也是优化。如下图,如果从1开始走,依次走过1、2、3、4,则dfn[1]=1,dfn[2]=2,dfn[3]=3,dfn[4]=4。回溯到节点2后,它将尝试走4,发现dfn[4]>dfn[2],说明4不是2的祖先,所以没必要作下一步操作了。
(3)细节三
这个地方同样很让人疑惑。很多人觉得奇怪,为什么在上面low[x] = Math.min(low[x], low[to]),但是到了下面就是low[x] = Math.min(low[x], dfn[to])。我们尝试一下全部使用low[x] = Math.min(low[x], low[to])会有什么结果。如下图,如果从1开始走,走到先依次走过1、2、3,当走到3的时候,low[3]更新为low[1],即1。接着依次走过4、5,当走到5的时候,low[5]更新为low[3],即1。那么在回溯的过程中,4、3、2、1的low全部变成了1。
某非根节点u是割点的充分条件是其存在某个子节点v,使得low[v]>=dfn[u]。
对于5、4、3、2这几个非根节点来说,它们所有的子节点的low都小于它们自身的dfn。而对于1这个根节点来说,它不存在两个及以上的不通过1连通的子节点,所以最后找不到割点。但是用肉眼都可以看出来,3是一个割点。所以不可以全部都使用low[x] = Math.min(low[x], low[to])。

(4)细节四
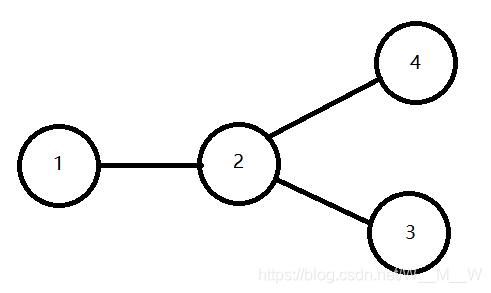
发现当前节点是割点以后,要等它遍历完它的所有子节点才能把它加入到cutPoints中,否则会出现重复。如下图,假如从1开始走,2会在cutPoints中出现两次,自己试一试吧。
四、总结
其实四条细节中,只有(2)和(3)具有普遍性,(1)和(4)是针对我个人的代码而言的,因为不同的编程方式具有不同的细节。如果有错误,欢迎指出。