姿态更新
捷联惯导数值更新算法通常可划分为姿态、速度和位置更新三部分﹐
姿态更新算法
是
核心
,其求解精度对整个捷联惯导的精度起着决定性的作用。目前主流的姿态更新求解方法是,先使用陀螺角增量的
多子样采样
计算等效旋转矢量,补偿转动不可交换误差,再使用等效旋转矢量计算姿态更新四元数。
地球自转角速度和牵连角速度
在考虑n系相对于i系的旋转时,一定要考虑这两部分:地球自转引起的n系旋转,以及惯导系统在地球表面附近移动因地球表面弯曲而引起的n系旋转

更新姿态

姿态更新可采用四元数连乘来实现
也可由严老师书中提到的方向余弦矩阵计算得到

速度更新
比力方程
比力方程是在地球表面附近进行惯性导航解算的基本方程

上式后两项可统称为有害加速度。比力方程式表明,只有在加速度计输出中扣除有害加速度后,才能获得运载体在导航系下的几何运动加速度,对加速度积分一次可得速度,再积分一次可得位置。因此,比力方程是惯导解算的基本方程。
PSINS源码
严老师在PSINS中也给出了相应的代码,计算了有害加速度
function eth = ethupdate(eth, pos, vn)
% Update the Earth related parameters, much faster than 'earth'.
%
% Prototype: eth = ethupdate(eth, pos, vn)
% Inputs: eth - input earth structure array
% pos - geographic position [lat;lon;hgt]
% vn - velocity
% Outputs: eth - parameter structure array
%
% See also ethinit, earth.
% Copyright(c) 2009-2014, by Gongmin Yan, All rights reserved.
% Northwestern Polytechnical University, Xi An, P.R.China
% 23/05/2014
if nargin==2, vn = [0; 0; 0]; end
eth.pos = pos; eth.vn = vn;
eth.sl = sin(pos(1)); eth.cl = cos(pos(1)); eth.tl = eth.sl/eth.cl;
eth.sl2 = eth.sl*eth.sl; sl4 = eth.sl2*eth.sl2;
sq = 1-eth.e2*eth.sl2; RN = eth.Re/sqrt(sq);
eth.RNh = RN+pos(3); eth.clRNh = eth.cl*eth.RNh;
eth.RMh = RN*(1-eth.e2)/sq+pos(3);
% eth.wnie = [0; eth.wie*eth.cl; eth.wie*eth.sl];
eth.wnie(2) = eth.wie*eth.cl; eth.wnie(3) = eth.wie*eth.sl;
% eth.wnen = [-vn(2)/eth.RMh; vn(1)/eth.RNh; vn(1)/eth.RNh*eth.tl];
eth.wnen(1) = -vn(2)/eth.RMh; eth.wnen(2) = vn(1)/eth.RNh; eth.wnen(3) = eth.wnen(2)*eth.tl;
% eth.wnin = eth.wnie + eth.wnen;
eth.wnin(1) = eth.wnie(1) + eth.wnen(1); eth.wnin(2) = eth.wnie(2) + eth.wnen(2); eth.wnin(3) = eth.wnie(3) + eth.wnen(3);
% eth.wnien = eth.wnie + eth.wnin;
eth.wnien(1) = eth.wnie(1) + eth.wnin(1); eth.wnien(2) = eth.wnie(2) + eth.wnin(2); eth.wnien(3) = eth.wnie(3) + eth.wnin(3);
% eth.gn = [0;0;-eth.g];
eth.g = eth.g0*(1+5.27094e-3*eth.sl2+2.32718e-5*sl4)-3.086e-6*pos(3); % grs80
eth.gn(3) = -eth.g;
% eth.gcc = eth.gn - cros(eth.wnien,vn); % Gravitational/Coriolis/Centripetal acceleration
% eth.gcc = [ eth.wnien(3)*vn(2)-eth.wnien(2)*vn(3); % faster than previous line
% eth.wnien(1)*vn(3)-eth.wnien(3)*vn(1);
% eth.wnien(2)*vn(1)-eth.wnien(1)*vn(2)+eth.gn(3) ];
eth.gcc(1) = eth.wnien(3)*vn(2)-eth.wnien(2)*vn(3);
eth.gcc(2) = eth.wnien(1)*vn(3)-eth.wnien(3)*vn(1);
eth.gcc(3) = eth.wnien(2)*vn(1)-eth.wnien(1)*vn(2)+eth.gn(3);
双子样假设
本篇博文以双子样算法为例,推导速度更新方程。
双子样假设:[
tk-2,tk]
时段内角速度观测量和比力观测量均
随时间线性变化
。如
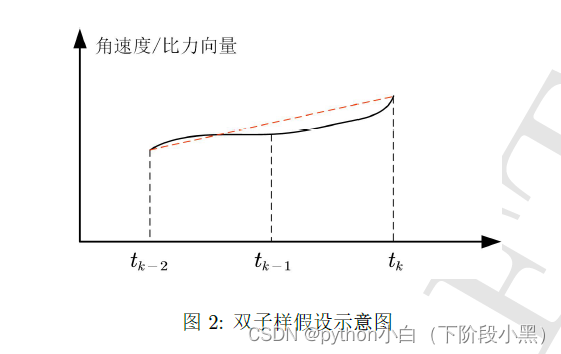
图2
所示,在两个采样区间内,将实际的角速度和比力(黑色曲线)近似为随时间线性变化(曲线简化为直线,红色虚线,黑色曲线下的积分面积为惯性传感器实际输出的角增量或速度增量)。上式表明,线性假设的系数 a、b、c、d不但决定了角速度和比力的
大小
,同时还决定了其
方向
,也即线性假设也考虑了角速度向量和比力向量的方向变化。
如下是双子样假设下的角速度和比力随时间变化函数
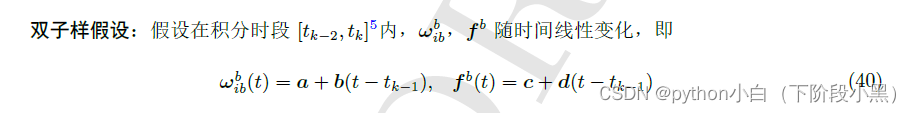
速度更新算法
速度更新中,有两项积分非常重要,一个是比力积分项,另一个就是重力/哥式积分项

那么可推导出双子样速度更新公式:
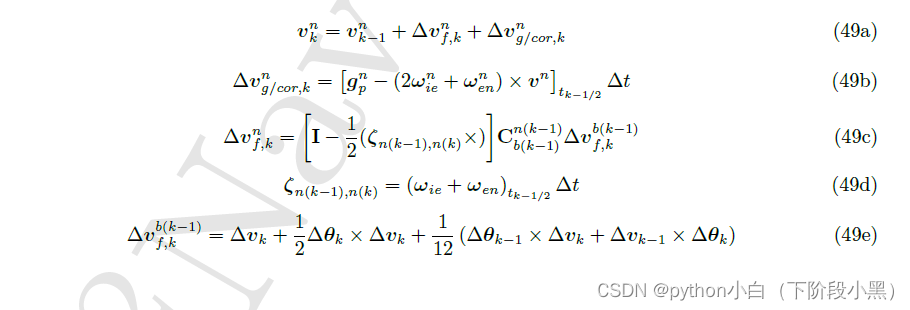
对于中间时刻(前一时刻和当前时刻的中间时刻)的速度求解,可采用线性外推方法:

对位置也可进行如上外推。
划桨误差补偿算法
下式描述的运动与现实生活划船中的划桨运动状况非常相似:一方面桨绕船身的横轴做往复角运动,另一方面船身连带船桨沿纵轴做间歇性加速线运动。可见,划船过程中船桨同时存在周期性的角运动和线运动,因此形象地称下式所描述的运动为划桨运动(
sculling motion
)。
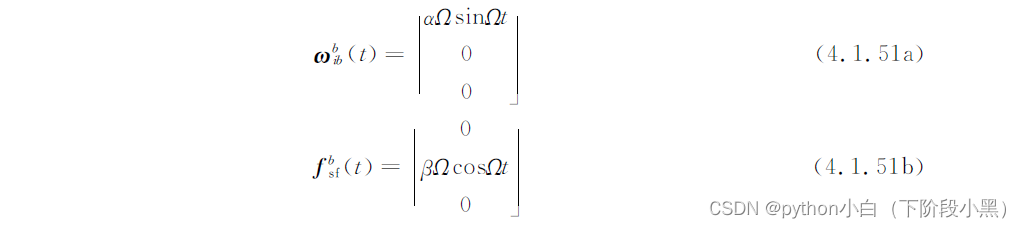
推导可得N子样划桨误差补偿算法:

PSINS源码
严老师同样在源码中给出了这个算法:
if coneoptimal==0
scullm = [0, 0, 0];
else
scullm = 1/12*(cros(glv.wm_st,vm)+cros(glv.vm_st,wm)); glv.wm_st = wm; glv.vm_st = vm;
end
else
vmm = sum(vm,1);
if coneoptimal==0
sm = glv.cs(n-1,1:n-1)*vm(1:n-1,:);
scullm = (cros(cm,vm(n,:))+cros(sm,wm(n,:)));
else % else: using polynomial fitting sculling compensation method
scullm = scullpolyn(wm, vm);
end
end
其中
sm = glv.cs(n-1,1:n-1)*vm(1:n-1,:);
scullm = (cros(cm,vm(n,:))+cros(sm,wm(n,:)));
这一块代码,为N子样划桨误差补偿算法的实现
位置更新
计算公式
可采用严老师书中的公式计算

也可参考牛老师的讲义中的公式

但需要注意的是,不同的公式,对应的不同的b系得定义,严老师定义东北天为正,牛老师定位北东地为正
PSINS源码
严老师在源码中也给出了相应得矩阵形式
ins.Mpv = [0, 1/ins.eth.RMh, 0; 1/ins.eth.clRNh, 0, 0; 0, 0, 1];
ins.MpvCnb = ins.Mpv*ins.Cnb; ins.Mpvvn = ins.Mpv*ins.vn;