一、DFS的概念
DFS的定义
DFS(Depth-First Search)
深度优先搜索,是一种常用的图遍历算法,用于在图或树数据结构中遍历所有节点。
DFS的搜索方式
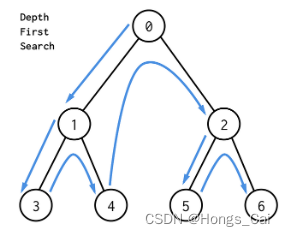
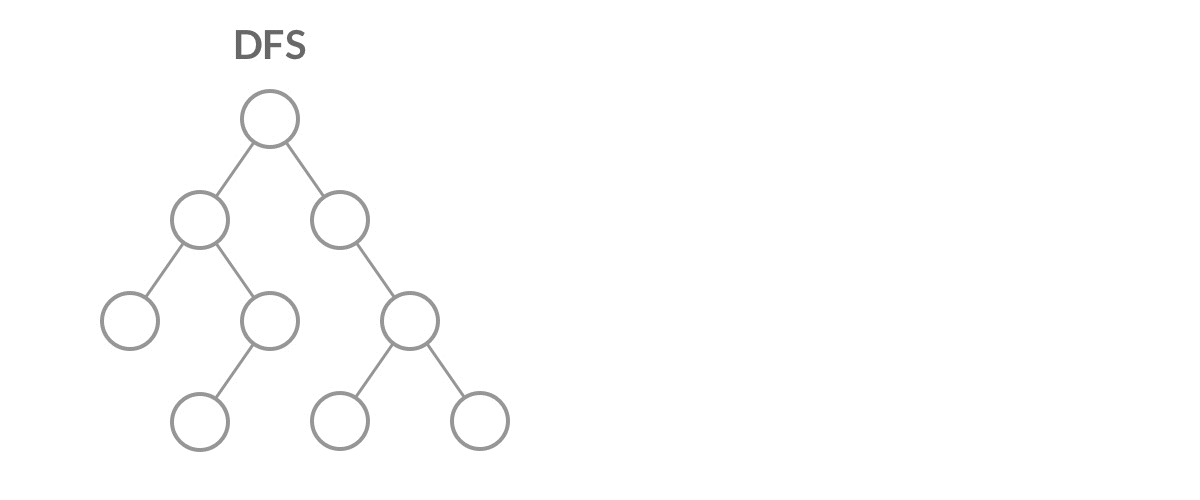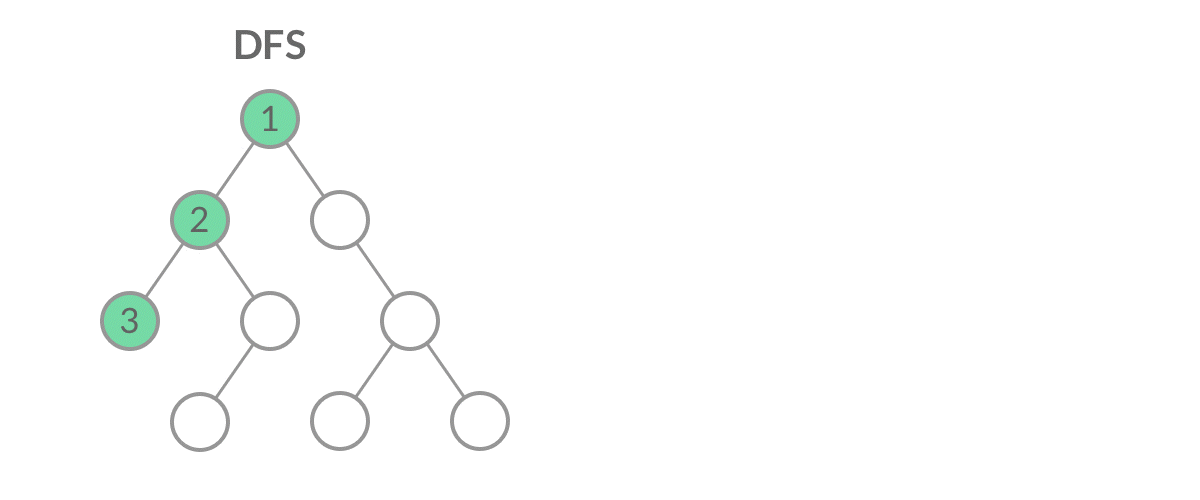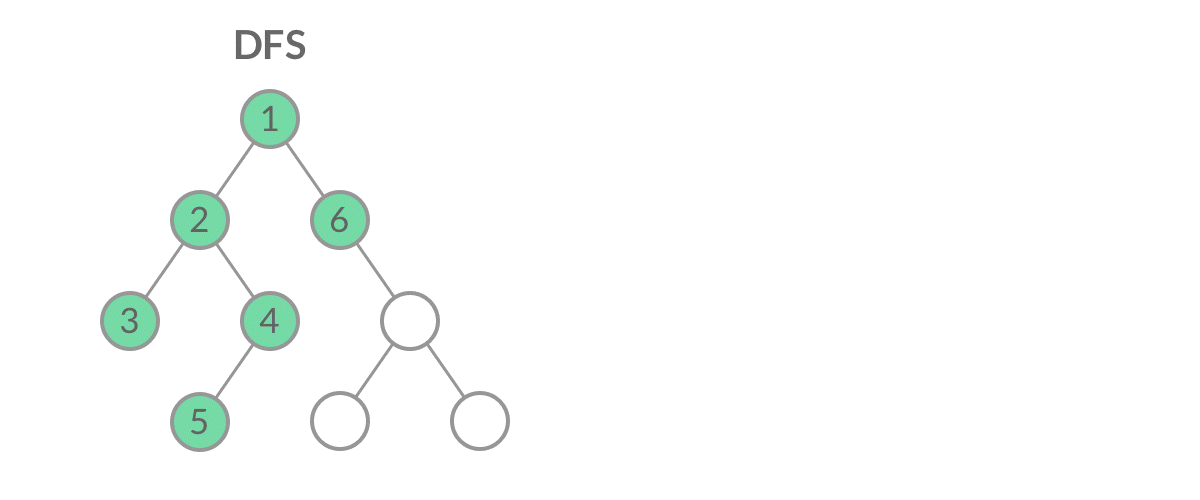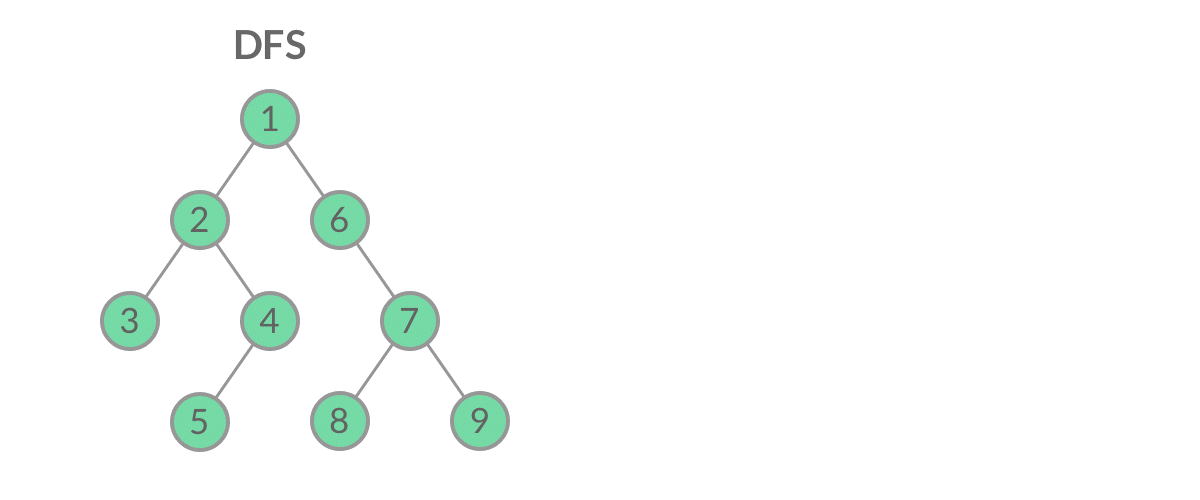
深度优先搜索从一个起始节点开始,沿着一条路径尽可能远地访问节点,直到到达不能继续前进的节点,然后返回上一层继续探索其他路径。这个过程是递归的,通过不断地深入进入节点的子节点,直到遍历完整个图。
DFS采用的数据结构
深度优先搜索使用
栈(Stack)
数据结构来保存需要探索的节点。
每次访问一个节点时,将其标记为已访问,并将其未访问的邻居节点压入栈中。然后从栈中弹出一个节点,继续访问该节点的未访问邻居节点,直到栈为空。
空间复杂度:
O
(
n
)
O(n)
O
(
n
)
DFS的特点
DFS不保证找到最短路径。
因为它首先沿着一条路径尽可能远地深入。如果需要找到最短路径,可以考虑使用其他算法,如广度优先搜索(BFS)或 Dijkstra 算法。一般最小步数、最短距离、最小操作次数等问题采用BFS。思路奇怪或是对空间要求高的使用深度优先搜索(DFS)。
DFS 在解决许多图论问题和遍历问题上非常有用,如查找图中的路径、连通性检测、拓扑排序等。它也可以应用于树的遍历,例如先序遍历、中序遍历和后序遍历。
二、DFS的实战应用
1.排列数字
题目描述:
给定一个整数
n
n
n
,将数字
1
∼
n
1∼n
1
∼
n
排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式:
共一行,包含一个整数
n
n
n
。
输出格式:
按字典序输出所有排列方案,每个方案占一行。
数据范围:
1
≤
n
≤
7
1≤n≤7
1
≤
n
≤
7
输入样例:
3
输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
实现思路
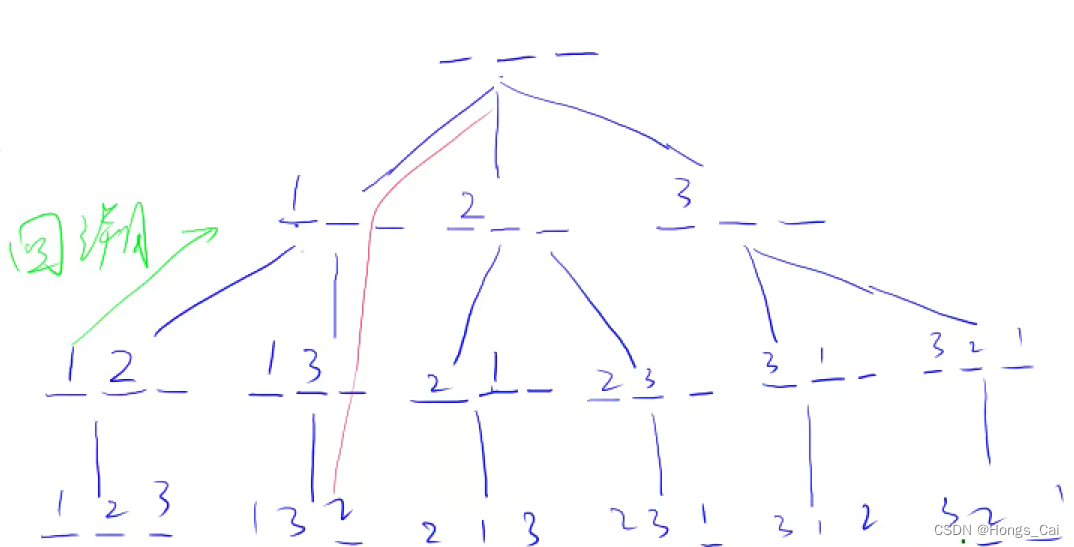
代码实现:
1.使用bool类型数组来表示是否占用
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 10;
int n, path[N];
bool st[N]; // 状态数组
void dfs(int u) // 第几个数字,一共几个数字
{
if (u == n)// 递归到最后一个数字
{
for (int i = 0; i < n; i++) cout << path[i] << ' '; // 输出保存的结果
puts(" ");
}
for (int i = 1; i <= n; i++)
if (!st[i]) // 没有被用过的数
{
path[u] = i;
st[i] = true; // i被用过
dfs(u + 1);// 走到下一层
st[i] = false;// 恢复现场
}
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n;
dfs(0);
return 0;
}
2.使用整型变量补码的每位来表示是否占用
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N = 10;
int n, path[N];
void dfs(int u, int state) // 第几个数字,一共几个数字
{
if (u == n)// 递归到最后一个数字
{
for (int i = 0; i < n; i++) cout << path[i] << ' '; // 输出保存的结果
puts(" ");
}
for (int i = 0; i < n; i++)
if (!(state >> i & 1)) // 没有被用过的数
{
path[u] = i + 1;
dfs(u + 1, state + (1 << i));
}
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n;
dfs(0, 0);
return 0;
}
2.n-皇后问题
题目描述:
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数
n
n
n
,请你输出所有的满足条件的棋子摆法。
输入格式共一行,包含整数
n
n
n
。
输出格式:
每个解决方案占
n
n
n
行,每行输出一个长度为
n
n
n
的字符串,用来表示完整的棋盘状态。
其中, 表示某一个位置的方格状态为空,
Q
Q
Q
表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围:
1
≤
n
≤
9
1≤n≤9
1
≤
n
≤
9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
代码实现:
//在此处,为了模拟坐标轴,使用u替换y,使用i替换x
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N=20;//此处x轴和y轴的长度为10,开20是大了,但是对角线长度约1.414*10(根号2),所以数组开大有好处
int n;//此处存储输入的行数&列数,
char q[N][N];//构建棋盘,大一些没坏处,注意类型需要为char(一开始无语写了个int)
bool col[N],dg[N],udg[N];//col是Column(列)的缩写,dg是diagonal(对角)的缩写,(反对角线前面的u想不出了)
//设udg的方程为y=x+b则b=y-x,替换后b=u-i,防止出现负数,则加上n,则有b=u+n-i(其实b=n+i-u也可,目的是一个对角线能单独映射)
//设dg的方程为y=-x+b,b=y+x,替换后b=i+u,perfect
void dfs(int u){//已经操作了u行
if(u==n){//好家伙,已经操作完u行了,一个输出了
for(int i=0;i<n;i++){
cout<<q[i]<<endl;
}
cout<<endl;
/*这种写法也可,但是如果上面的看不懂建议补习C语言基础
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cout<<q[i][j];
}
cout<<endl;
}
cout<<endl;
*/
return;
}
for(int i=0;i<n;i++){//到这一步说明还没有dfs搜索完
if(!col[i] and !dg[i+u] and !udg[u+n-i]){//这个点在各种映射下都是合法的
q[u][i]='Q';
col[i]=dg[i+u]=udg[u+n-i]=true;//这些点用掉啦
dfs(u+1);//继续往下一层探
q[u][i]='.';
col[i]=dg[i+u]=udg[u+n-i]=false;//出来后这些点恢复原状
}
}
}
int main(){
cin>>n;//输入行数
for(int i=0;i<n;i++){//搭建一个“船新”的棋盘
for(int j=0;j<n;j++){
q[i][j]='.';
}
}
dfs(0);//0代表目前已经操作了0行,并且需要对第1行进行操作(在数组中映射为0行)
return 0;
}