作者:Elliott Saslow
翻译:老齐
与本文相关的图书推荐:《Python大学实用教程》

众所周知,斐波那契数列是一种非常重要的数列。
0,1,1,2,3,4,8,13,21,34,55,…
用递归的方式,可以这样定义斐波那契数列:
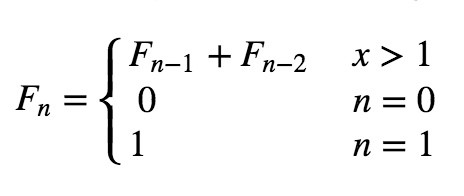
按照上面的公式,可以用Python语言直接写出实现它的函数:
def fib_recursive(n):
if n == 0: return 0
if n == 1: return 1
else: return(fib_recursive(n-1)+fib_recursive(n-2))
不管什么时候,我们遇到某个算法的实现,总要问一问下面的问题:
正确吗?正确
耗时多少?
是否可以改进?可以
现在,无需深入了解具体细节,用递归方式,属于贪心算法,需要花费大量计算步骤来完成。因此,让我们尝试使用列表来完成此操作,下面的方法可以加快处理速度并简化计算。
def fib_poly(n):
#注意0
if n == 0:
return 0
#用列表保存数值
else:
f = np.zeros(n+1)
f[0] = 0
f[1] = 1
for i in range(2,n+1):
f[i] = f[i-1] + f[i-2]
return f[n]
Ok,来看看它的表现。下图显示了执行上面两个函数的所用时间比较。

哇!注意观察它们所用时间的差别!后面这个函数比前面的递归方法快多了。
下面的图示中很明显地表示了二者执行时间的差异。

哇! 令人难以置信,递归居然如此慢。还有更快的方法呢? 应该有:
如下所示,可以用矩阵的方法计算斐波那契数列,会更快。

import numpy as np
def fib_matrix(n):
Matrix = np.matrix([[0,1],[1,1]])
vec = np.array([[0],[1]])
return np.matmul(Matrix**n,vec)
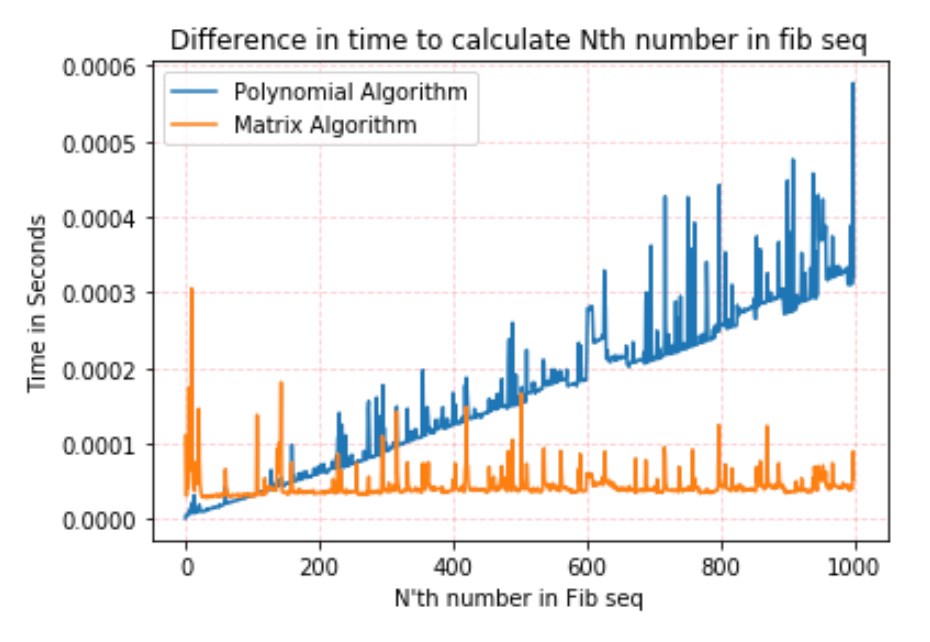
这真的很酷,在整个测试过程中,矩阵算法在几乎恒定的时间内执行。关于用矩阵实现斐波那契数列的方法,可以参考 《跟老齐学Python:数据分析》 ,书中有相关说明。
注: 此外,斐波那契数列还能够用生成器、迭代器方式实现,这些实现方法,可以到 《Python大学实用教程》 查阅。