二分查找树(binary search tree)

今天开始我们就会进入一些数据结构的部分了。今天第一个要讲的是一类特殊的数据结构，二分查找树。二分查找树的特点如下：

即根节点的数值一定小于左右子节点，其优势在于插入与查找时间较低为
$\mathcal{O}(n\log n)$

同样，我们比较关心二分查找树的创建插入删除

首先说一下，我们在创建二分查找树的时候，也可以根据根节点数值小于子节点的规则一个一个的插入。所以创建与插入可以看成一起的。插入的时候也很简单，就是根据上述的特点，去找到一个比需要插入的值更小的根节点，然后看看插入到左节点还是右节点合适(还要考虑到后面的节点)，直接插入即可。

这里我们主要要聊一下删除的问题：

删除某一个节点的规则稍微复杂一点：

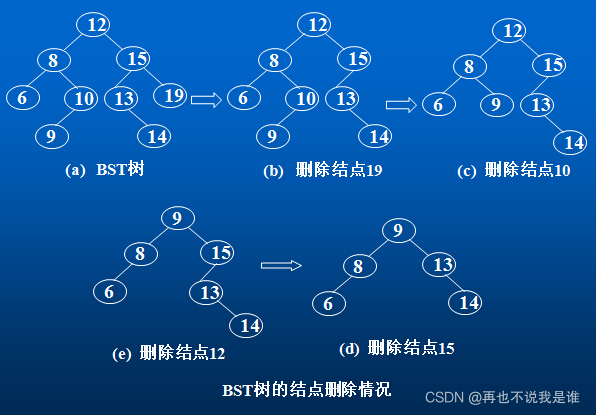
①若p是叶子结点：直接删除p，如图(b)所示。

② 若p只有一棵子树(左子树或右子树)：直接用p的左子树(或右子树)取代p的位置而成为f的一棵子树。即原来p是f的左子树，则p的子树成为f的左子树；原来p是f的右子树，则p的子树成为f的右子树，如图(c)、 (d)所示。

③ 若p既有左子树又有右子树：处理方法有以下两种，可以任选其中一种。

◆ 用p的直接前驱结点代替p。即从p的左子树中选择值最大的结点s放在p的位置(用结点s的内容替换结点p内容)，然后删除结点s。s是p的左子树中的最右边的结点且没有右子树，对s的删除同②，如图(e)所示。

◆ 用p的直接后继结点代替p。即从p的右子树中选择值最小的结点s放在p的位置(用结点s的内容替换结点p内容)，然后删除结点s。s是p的右子树中的最左边的结点且没有左子树，对s的删除同②。

关于二分查找树的内容就这么多。主要是删除操作，其他的操作也是比较好理解的。