吴恩达测试
测试一
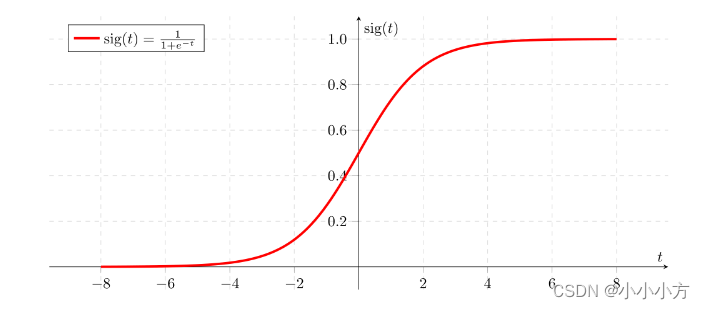
import math
from public_tests import *
def basic_sigmoid(x):
s = 1./(1+np.exp(-x))
return s
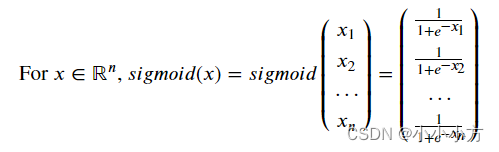
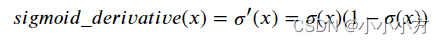
def sigmoid_derivate(x):
s = sigmoid(x)
ds = s*(1-s)
return ds
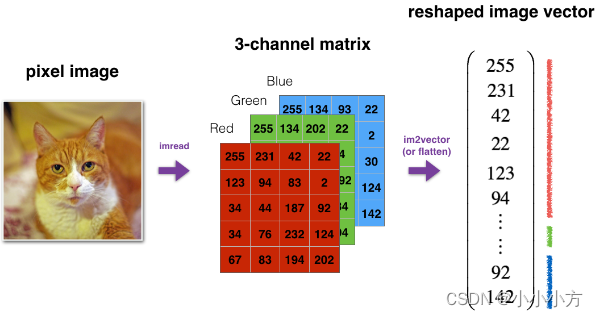
def image2vector(image):
v = image.reshape(image.shape[0]*image.shape[1].image[2],1)
return v
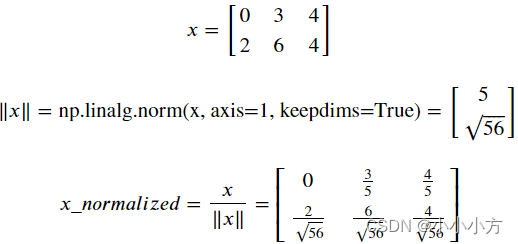
def normalize_rows(x):
x_norm = None
x_norm = np.linalg.norm(x,ord=2,axis=1,keepdims=True)
x = x/x_norm
return x

def softmax(x):
x_exp = np.exp(x)
x_sum = np.sum(x_exp,axis=1,keepdims=True)
s = x_exp/x_sum
return s
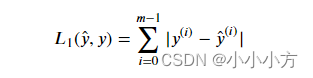
def L1(yhat,y):
loss = sum(abs(yhat-y))
return losss
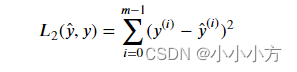
def L2(yhat,y):
loss = np.dot((yhat-y),(yhat-y))
return loss
测试二
只限于理解,实现是缺少对应的包和数据的
# 导入数据
X,Y = load_planar_dataset()
# 矩阵重塑
shape_X = X.shape #(2,400)
shape_Y = Y.shape #(1,400)
m = shape_X[1] # 400
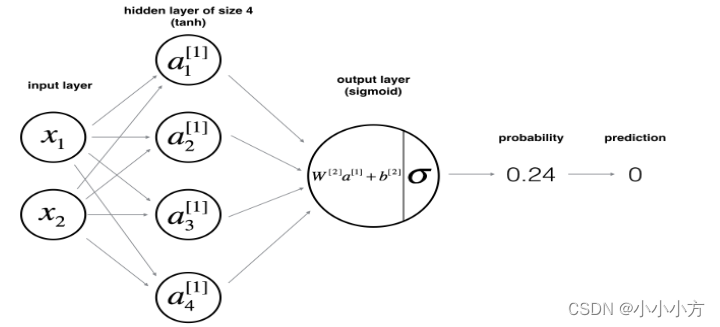

# 定义每层的参数
def layer_sizes(X,Y):
n_x = X.shape[0]
n_h = 4
n_y = Y.shape[0]
return(n_x,n_h,h_y)
# 初始花参数
def initialize_parameters(n_x,n_h,n_y):
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1)))
parameters = ["W1":W1,
"W2":W2,
"b1":b1,
"b2":b2]
return parameters
# 前向传播
def forward_propagation(X,parameters):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(W1,X)+b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2,A1)+b2
A2 = sigmoid(Z2)
cache = {"Z1":Z1,
"Z2":Z2,
"A1":A1,
"A2":A2}
return A2,cache
# 损失函数
def compute_cost(A2,Y):
m = Y.shape[1]
logprobs = np.multiply(np.log(A2),Y)+np.multiply((1-Y),np.log(1-A2))
cost = -np.sum(logprobs)/m
return cost

def backward_propagation(parameters,cache,X,Y):
m =X.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2 = A2 - Y
dW2 = np.dot(dZ2,A1.T)*(1/m)
db2 = np.sum(dZ2,axis = 1,keepdims = True)*(1/m)
dZ1 = dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1,2))
dW1 = np.dot(dZ1,X.T)*(1/m)
db1 = np.sum(dZ1,axis = 1,keepdims = True)*(1/m)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
# 更新权重
def update_parameters(parameters,grads,learning_rate = 1.2):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
dW1 = grads["dW1"]
dW2 = grads["dW2"]
db1 = grads["db1"]
db2 = grads["db2"]
W1 = W1 -learning_rate *dW1
W2 = W2 -learning_rate *dW2
b1 = b1 - learning_rate *db1
b2 = b2 - learning_rate *db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
# 创建模型
def nn_model(X,Y,n_h,num_iterations=10000,print_cost=False):
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
for i in range(0, num_iterations):
A2, cache = forward_propagation(X, parameters)
cost = compute_cost(A2, Y)
grads = backward_propagation(parameters, cache, X, Y)
parameters = update_parameters(parameters, grads, learning_rate=1.2)
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters
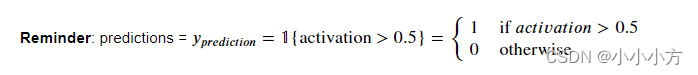
def predict(parameters,X):
A2, cache = forward_propagation(X, parameters)
predictions = (A2>0.5)
return predictions
测试三
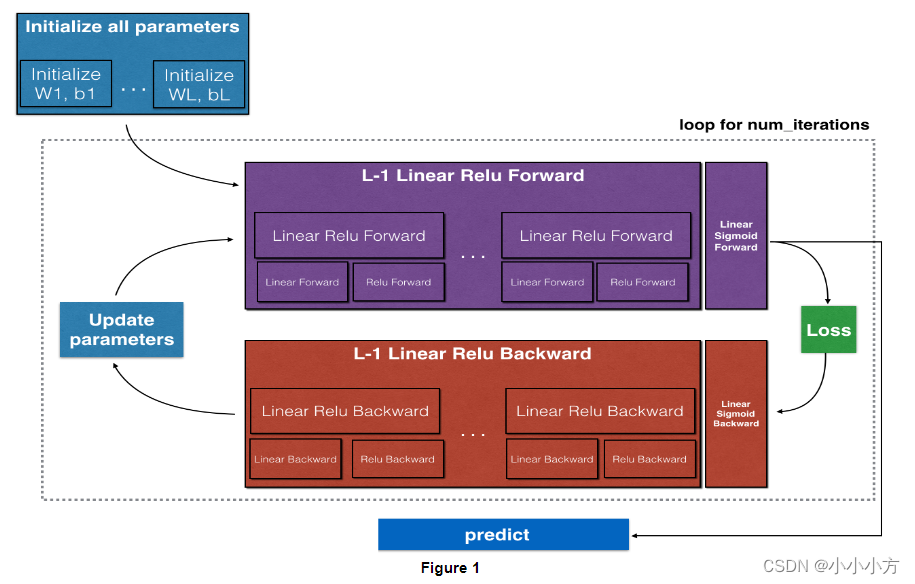
# 初始化
def initialize_parameters(n_x,n_h,n_y):
np.random.seed(1)
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
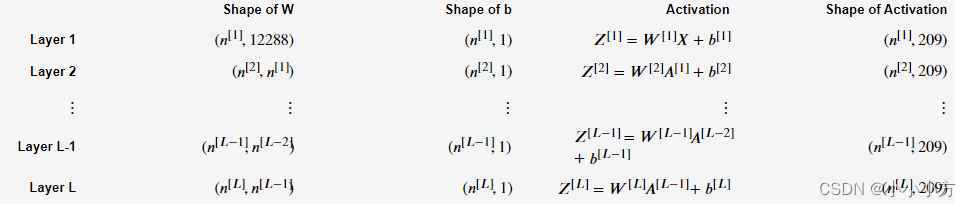

# 深层初始化
def initialize_parameters_deep(layer_dims):
np.random.seed(3)
parameters = {}
L = len(layer_dims) # number of layers in the network
for l in range(1, L):
parameters["W" + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
parameters["b" + str(l)] = np.zeros((layer_dims[l], 1))
return parameters

# 前向传播 A[0] = x
def linear_forward(A,W,b):
Z = np.dot(W,A)+b
cache = (A, W, b)
return Z, cache

def linear_activation_forward(A_prev,W,b,activation):
if activation == "sigmoid":
Z,linear_cache = linear_forward(A_prev,W,b)
A,activation_cache = sigmoid(Z)
elif activation == "relu":
Z,linear_cache = linear_forward(A_prev,W,b)
A,activation_cache = relu(Z)
cache = (linear_cache, activation_cache)
return A, cache
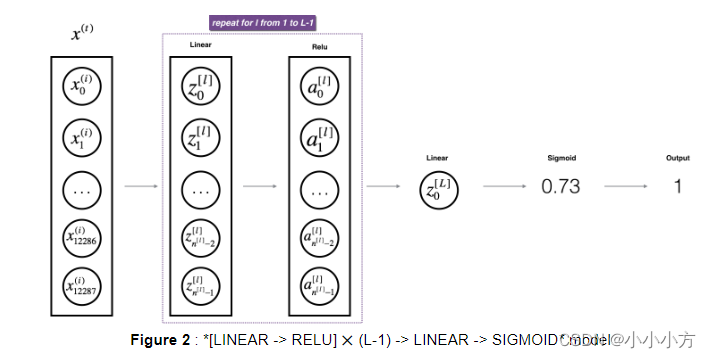
# 深层前向传播
def L_model_forward(X, parameters):
caches = []
A = X
L = len(parameters) // 2 # number of layers in the neural network
for l in range(1, L):
A_prev = A
A,cache = linear_activation_forward(A_prev,parameters['W'+str(l)],parameters['b'+str(l)],"relu")
caches.append(cache)
AL,cache = linear_activation_forward(A,parameters['W'+str(L)],parameters['b'+str(L)],"sigmoid")
caches.append(cache)
return AL, caches
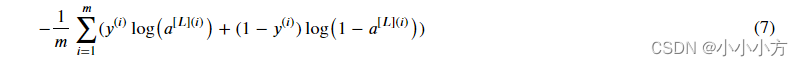
def compute_cost(AL, Y):
m = Y.shape[1]
logprobs = np.multiply(np.log(AL),Y)+ np.multiply((1-Y),np.log(1-AL))
cost = - np.sum(logprobs)/m
return cost
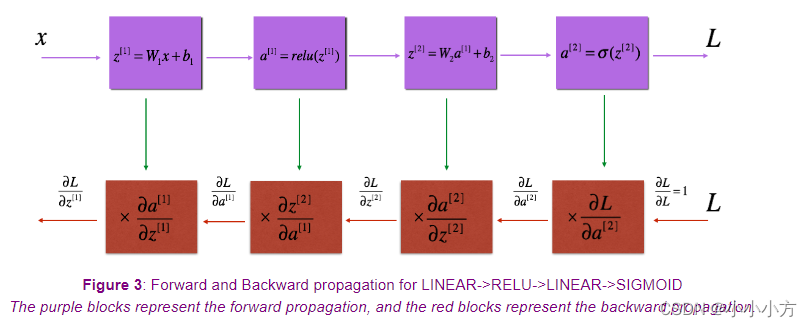
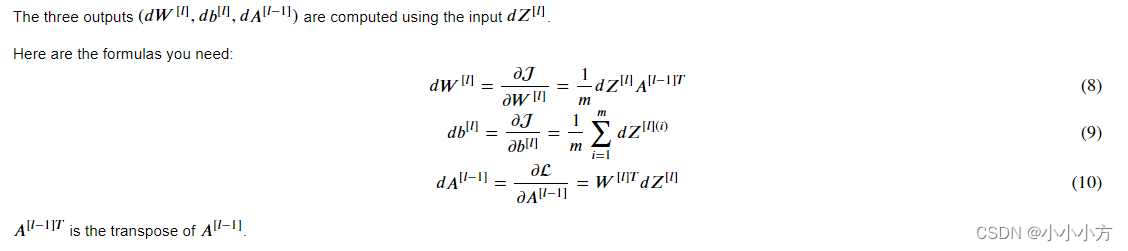
# 反向传播
def linear_backward(dZ, cache):
A_prev, W, b = cache
m = A_prev.shape[1]
dW = 1 / m * np.dot(dZ, cache[0].T)
db = 1 / m * np.sum(dZ, axis = 1, keepdims = True)
dA_prev = np.dot(cache[1].T, dZ)
return dA_prev, dW, db

# 线性激活层反向传播
def linear_activation_backward(dA, cache, activation):
linear_cache, activation_cache = cache
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
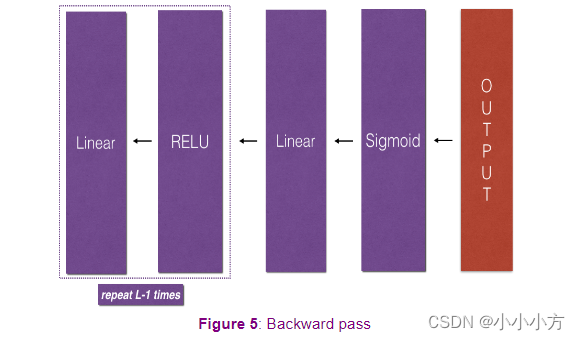
#L层的反向传播
def L_model_backward(AL, Y, caches):
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache=caches[-1]
dA_prev_temp, dW_temp, db_temp =linear_activation_backward(dAL,current_cache,activation="sigmoid")
grads["dA"+str(L-1)]=dA_prev_temp
grads["dW"+str(L)]=dW_temp
grads["db"+str(L)]=db_temp
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp =linear_activation_backward( grads["dA" + str(l+1)] , current_cache, "relu")
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] =dW_temp
grads["db" + str(l + 1)] =db_temp
return grads

# 参数更新
def update_parameters(params, grads, learning_rate):
parameters = params.copy()
L = len(parameters) // 2 # number of layers in the neural network
for l in range(L):
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
测试四
train_x_orig, train_y, test_x_orig, test_y, classes = load_data()
m_train = train_x_orig.shape[0] #209
num_px = train_x_orig.shape[1] #64
m_test = test_x_orig.shape[0] #50
Number of training examples: 209
Number of testing examples: 50
Each image is of size: (64, 64, 3)
train_x_orig shape: (209, 64, 64, 3)
train_y shape: (1, 209)
test_x_orig shape: (50, 64, 64, 3)
test_y shape: (1, 50)
# reshape
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T
train_x's shape: (12288, 209)
test_x's shape: (12288, 50)
# 两层神经网络
n_x = 12288 # num_px * num_px * 3
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)
learning_rate = 0.0075
def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
np.random.seed(1)
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
(n_x, n_h, n_y) = layers_dims
# 参数初始化
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
for i in range(0, num_iterations):
# 正向传播
A1,cache1 = linear_activation_forward(X,W1,b1,"relu")
A2,cache2 = linear_activation_forward(A1,W2,b2,"sigmoid")
# 代价函数
cost = compute_cost(A2,Y)
# 初始化反向传播
dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
# 反向传播
dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
grads['dW1'] = dW1
grads['db1'] = db1
grads['dW2'] = dW2
grads['db2'] = db2
# 参数更新
parameters = update_parameters(parameters, grads, learning_rate)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# 输出代价函数
if print_cost and i % 100 == 0 or i == num_iterations - 1:
print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
if i % 100 == 0 or i == num_iterations:
costs.append(cost)
return parameters, costs
# 训练模型
parameters, costs = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True)
#预测
predictions_train = predict(train_x, train_y, parameters)
predictions_test = predict(test_x, test_y, parameters)
# L层神经网络 L=4
layers_dims = [12288, 20, 7, 5, 1]
def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
np.random.seed(1)
costs = []
parameters = initialize_parameters_deep(layers_dims)
for i in range(0, num_iterations):
AL, caches = L_model_forward(X, parameters)
cost = compute_cost(AL, Y)
grads = L_model_backward(AL, Y, caches)
parameters = update_parameters(parameters, grads, learning_rate)
if print_cost and i % 100 == 0 or i == num_iterations - 1:
print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
if i % 100 == 0 or i == num_iterations:
costs.append(cost)
return parameters, costs
# 训练模型
parameters, costs = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)
# 预测模型
pred_train = predict(train_x, train_y, parameters)
pred_test = predict(test_x, test_y, parameters)
版权声明:本文为weixin_56368033原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。