第15章动态规划_思考题
概要
题目很多但是每题都很经典,有的题目确实是想了很久也没有一个合理的解答(可以说过程很痛苦),故有部分答案是参照别人的做法。有一部分是根据自己的理解来解题,不足之处会慢慢修改。
15.1 有向无环图中的最长简单路径
给定一个有向无环图G=(V,E),边权重为实数,给定图中两个顶点s和t。设计动态规划算法,求从s到t的最长加权简单路径。子问题图是怎么样的?算法的效率如何?
15.2 最长回文子序列
回文是正序和逆序列相同的非空字符串。例如,所有长度为1的字符串、civic、raqcecar、aibohphpbia都是回文。
设计高效算法,求给定输入字符串的最长回文子序列。例如,给定输入character,算法应该返回carac。算法的运行时间是怎样的?
两种思路,比较偷懒的做法是已知数组a,先把它的倒序用数组b保存,再求a和b的最长公共子序列。
还有一个思路如下:
先构建最优解的结构特征,m[i,j]表示从数组n的i序列出发到j序列的最长回文(0<=i<=j<=n)。
递归式如下:
m
[
i
,
j
]
=
{
1
若i=j
1
若i=j-1且a[i]!=a[j]
2
若i=j-1且a[i]=a[j]
m
a
x
(
m
[
i
+
1
,
j
]
,
m
[
i
,
j
−
1
]
)
若i<j-1且a[i]!=a[j]
m
[
i
+
1
,
j
−
1
]
+
2
若i<j-1且a[i]=a[j]
m[i,j]= \begin{cases} 1& \text{若i=j}\\ 1& \text{若i=j-1且a[i]!=a[j]}\\ 2& \text{若i=j-1且a[i]=a[j]}\\ max(m[i+1,j],m[i,j-1])& \text{若i<j-1且a[i]!=a[j]}\\ m[i+1,j-1] + 2& \text{若i<j-1且a[i]=a[j]}\\ \end{cases}
m
[
i
,
j
]
=
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎧
1
1
2
m
a
x
(
m
[
i
+
1
,
j
]
,
m
[
i
,
j
−
1
]
)
m
[
i
+
1
,
j
−
1
]
+
2
若
i=j
若
i=j-1
且
a[i]!=a[j]
若
i=j-1
且
a[i]=a[j]
若
i<j-1
且
a[i]!=a[j]
若
i<j-1
且
a[i]=a[j]
代码如下:
static void Main(string[] args)
{
var text = "character";
var charArray = text.ToArray();
int[,] m = new int[charArray.Length, charArray.Length];
string[,] s = new string[charArray.Length, charArray.Length];
for (var i = 0; i < charArray.Length; i++)
{
m[i, i] = 1;
}
var r = Execute(charArray, m, s, 0, charArray.Length - 1);
PrintPalindrome(charArray, s, r, 0, charArray.Length - 1);
}
/// <summary>
/// 最长回文子序列(自顶向下带备忘录)
/// </summary>
/// <param name="ca">原字符串数组</param>
/// <param name="m">长度存放数组</param>
/// <param name="i">起点下标</param>
/// <param name="j">终点下标</param>
/// <returns></returns>
public static int Execute(char[] ca, int[,] m, string[,] s, int i, int j)
{
if (i > j)
{
return 0;
}
if (m[i, j] > 0)
{
return m[i, j];
}
if (ca[i] != ca[j])
{
var r_1 = Execute(ca, m, s, i + 1, j);
var r_2 = Execute(ca, m, s, i, j - 1);
if (r_1 > r_2)
{
s[i, j] = "->";
m[i, j] = r_1;
return r_1;
}
else
{
s[i, j] = "<-";
m[i, j] = r_2;
return r_2;
}
}
else
{
s[i, j] = "-><-";
var r = Execute(ca, m, s, i + 1, j - 1) + 2;
m[i, j] = r;
return m[i, j];
}
}
/// <summary>
/// 打印回文
/// </summary>
/// <param name="ca">原字符串数组</param>
/// <param name="s">辅助表</param>
/// <param name="r">回文长度</param>
/// <param name="i">起点下标</param>
/// <param name="j">终点下标</param>
public static void PrintPalindrome(char[] ca, string[,] s, int r, int i, int j)
{
char[] p = new char[r];
var head = 0;
var tail = p.Length - 1;
while (i < j)
{
if (s[i, j] == "->")
{
i++;
}
else if (s[i, j] == "<-")
{
j--;
}
else if (s[i, j] == "-><-")
{
p[head++] = ca[i++];
p[tail--] = ca[j--];
}
}
if (i == j)
{
p[head] = ca[i];
}
for (var k = 0; k < p.Length; k++)
{
Console.Write(p[k]);
}
}
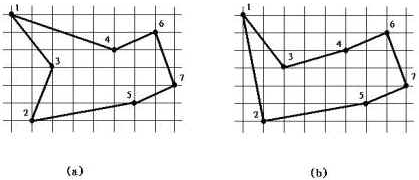
15.3 双向欧几里得旅行商问题
先扔代码上来,此题卡了很久,对于该题的分析在日后放出。
static void Main(string[] args)
{
Console.WriteLine("请输入坐标个数");
var count = Convert.ToInt32(Console.ReadLine());
var points = new Point[count];
for (var i = 0; i < count; i++)
{
Console.Write("请输入坐标" + (i + 1) + "的X值");
var x = Convert.ToDouble(Console.ReadLine());
Console.Write("请输入坐标" + (i + 1) + "的Y值");
var y = Convert.ToDouble(Console.ReadLine());
points[i] = new Point(x, y);
}
double[,] m = null;
int[,] s = null;
TSP_Length(points, ref m, ref s);
PrintTSP(points.Length, m, s);
}
#region "计算两点之间的欧几里得距离"
private static double GetDistance(Point[] points, int p1, int p2)
{
return Math.Sqrt((points[p1].X - points[p2].X) * (points[p1].X - points[p2].X)
+ (points[p1].Y - points[p2].Y) * (points[p1].Y - points[p2].Y));
}
#endregion
#region '快速排序'
public static void QuickSort(Point[] points,
int p, int r)
{
if (p >= r)
{
return;
}
var count = p - 1;
for (var i = p; i < r; i++)
{
if (points[i].X <= points[r].X)
{
count++;
}
}
var temp = points[++count];
points[r] = points[count];
points[count] = temp;
r = count;
QuickSort(points, p, count - 1);
QuickSort(points, count + 1, r);
}
#endregion
#region 'TSP算法'
/// <summary>
/// 计算TSP的长度
/// </summary>
/// <param name="points"></param>
/// <param name="m"></param>
/// <param name="s"></param>
public static void TSP_Length(Point[] points, ref double[,] m, ref int[,] s)
{
var count = points.Length;
QuickSort(points, 0, count - 1);
m = new double[count, count];
s = new int[count, count];
if (count > 2)
{
// case1
// i = j = count - 1
// i = count - 2 , j = count - 1
m[count - 1, count - 1] = 0;
m[count - 2, count - 1] = GetDistance(points, count - 2, count - 1);
s[count - 2, count - 1] = count - 1;
for (var i = count - 3; i >= 0; i--)
{
// case2
// i < j - 1
for (var j = count - 1; j > i + 1; j--)
{
m[i, j] = GetDistance(points, i, i + 1) + m[i + 1, j];
s[i, j] = i + 1;
}
// case3
// i = j - 1
var min = double.MaxValue;
for (var j = i + 2; j <= count - 1; j++)
{
var temp = m[i + 1, j] + GetDistance(points, i, j);
if (temp < min)
{
min = temp;
s[i, i + 1] = j;
}
}
m[i, i + 1] = min;
}
s[0, 0] = 1;
m[0, 0] = m[0, 1] + GetDistance(points, 0, 1);
}
}
/// <summary>
/// 构造TSP
/// </summary>
/// <param name="count"></param>
/// <param name="m"></param>
/// <param name="s"></param>
public static void PrintTSP(int count, double[,] m, int[,] s)
{
var left = 0;
var right = 0;
var next = 0;
for (var i = 0; i < count; i++)
{
next = s[left, right];
Console.WriteLine(left.ToString()
+ "to "
+ next.ToString());
if (left == right
&& left == 0)
{
right = 1;
}
else
{
if (left == right - 1)
{
left = left + 1;
right = next;
}
else if (left < right - 1)
{
left = left + 1;
}
}
}
}
#endregion
15.5 编辑距离
为了将一个文本串x[1…m] 转换为目标串y[1…n],我们可以使用多种变换操作。我们的目标是,给定x和y ,求将x转换为y的一个变换操作序列。我们使用一个数组z保存中间结果,假定它足够大,可存下中间结果的所有字符。初始时,z是空的;结束时,应有z[j]=y[j],j=1,2,…,n。我们维护两个下标i和j,分别指向x和y中的位置,变换操作允许改变z的内容和这两个下标。初始时,i=j=1。在转换过程中应处理x的所有字符,这意味着在变换操作结束时,应当有i=m+1。
我们可以使用如下6种变换操作:
复制(copy) — 从x复制当前字符到z,即进行赋值z[j]=x[i],并将两个下标i和j都增1。此操作处理了x[i]。
替换(replace) — 将x的当前字符x[i]替换为另一个字符c,然后进行赋值z[j]=c,并将两个下标i ii和j jj都增1。此操作处理了x[i]。
删除(delete) — 删除x中的当前字符x[i],即将i增1,j不变。此操作处理了x[i]。
插入(insert) — 将字符c插入z中,z[j]=c,将j 增1,i不变。此操作未处理x中的字符。
旋转(twiddle,即交换) — 将x xx中的当前字符和下一个字符复制到z中,但交换顺序,z[j]=x[i+1]且z[j+1]=x[i],将i和j都增2。此操作处理了x[i]和x[i+1]。
终止(kill) — 删除x中的剩余字符,令i=m+1。此操作处理了x xx中所有尚未处理的字符。如果执行此操作,则转换过程结束。
下面给出了将源字符串algorithm转换为目标字符串altruistic的一种变换操作序列,下划线指出执行一个变换操作后两个下标i和j的位置:
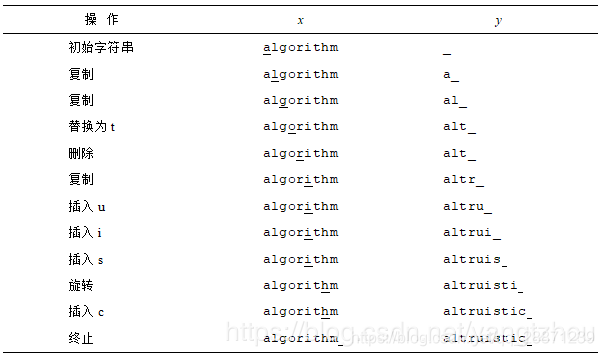
每个变换操作都有相应的代价。具体的代价依赖于特定的应用,但我们假定每个操作的代价是一个已知的常量。我们还假定复制和替换的代价小于删除和插入的组合代价,否则复制和替换操作就没有意义了。一个给定的变换操作序列的代价为其中所有变换操作的代价只和。在上例中,将algorithm转换为altruistic的代价为
(3·cost(复制))+ cost(替换) + cost(删除) + (4·cost(替换))+ cost(旋转) + cost(终止)
a.给定两个字符串x[1…m]和y[1…n]以及变换操作的代价,x到y编辑距离是将x转换为y的最小代价的变换操作序列的代价值。设计动态规划算法,求x[1…m]到[1…n]的编辑距离并打印最优变换操作序列。分析算法的时间和空间复杂度。
还是要先理解动态规划设计的通用模式,就如在15.3节中提到的:在确定最优解使用哪些子问题时,我们需要考察多少种选择。
在本题中我们同样要去考察,考察在字符串转换过程中下一步的所有可能选择:
1.当x[i] == y[i]时,此时我们下一步只做复制。
2.当x[i] != y[i]时,此时最优子结构必然是在replace、delete、insert、twiddle、kill中去选择,那么子问题就变成了replace、delete、insert、twiddle、kill搭配更小规模的两个字符串做转换。着重说下旋转,旋转的执行只有一定条件的,它是在当i和j都在可能范围内(i<=x.Length&&j<=y.Length)并且x[i+1] == y[j],x[i] == y[j+1]时才执行。
我们用r[i,j]来存储数组x,y在当前下标为i,j的情况下剩余转换的最小代价值。
static void Main(string[] args)
{
var s_str = "algorithm";
var d_str = "altruistic";
var z = new char[d_str.Length];
var r = new int[s_str.Length + 1, d_str.Length + 1];
var s = new string[s_str.Length + 1, d_str.Length + 1];
var value = Execute(s_str.ToArray(), d_str.ToArray(), z, 0, 0, r, s);
var i = 0;
var j = 0;
while (value > 0)
{
var str = string.Empty;
if (s[i, j] == "Copy")
{
i++;
j++;
str = "Copy";
}
else if (s[i, j] == "Replace")
{
i++;
j++;
str = "Replace";
}
else if (s[i, j] == "Delete")
{
i++;
str = "Delete";
}
else if (s[i, j] == "Insert")
{
j++;
str = "Insert";
}
else if (s[i, j] == "Twiddle")
{
i = i + 2;
j = j + 2;
str = "Twiddle";
}
else if (s[i, j] == "Kill")
{
i = s_str.Length;
str = "Kill";
}
Console.WriteLine(str);
value = r[i, j];
}
}
public static int Execute(char[] x, char[] y, char[] z,
int i, int j, int[,] r, string[,] s)
{
if (i == x.Length
&& j == y.Length)
{
r[i, j] = 0;
return 0;
}
if (r[i, j] > 0)
{
return r[i, j];
}
if (i == x.Length)
{
var cost = Execute(x, y, z, i, j + 1, r, s)
+ Insert(ref y, ref z, j);
s[i, j] = "Insert";
r[i, j] = cost;
return cost;
}
else if (j == y.Length)
{
var cost = Execute(x, y, z, x.Length, j, r, s)
+ Kill();
s[i, j] = "Kill";
r[i, j] = cost;
return cost;
}
var min = int.MaxValue;
int temp;
if (x[i] == y[j])
{
temp = Execute(x, y, z, i + 1, j + 1, r, s)
+ Copy(ref x, ref z, i, j);
min = temp < min ? temp : min;
s[i, j] = "Copy";
r[i, j] = temp;
return temp;
}
else
{
temp = Execute(x, y, z, i + 1, j + 1, r, s)
+ Replace(ref y, ref z, j);
min = temp < min ? temp : min;
s[i, j] = "Replace";
r[i, j] = min;
temp = Execute(x, y, z, i + 1, j, r, s)
+ Delete();
min = temp < min ? temp : min;
s[i, j] = "Delete";
r[i, j] = min;
temp = Execute(x, y, z, i, j + 1, r, s)
+ Insert(ref y, ref z, j);
min = temp < min ? temp : min;
s[i, j] = "Insert";
r[i, j] = min;
if (i <= x.Length - 2
&& j <= y.Length - 2)
{
if (x[i] == y[j + 1]
&& x[i + 1] == y[j])
{
temp = Execute(x, y, z, i + 2, j + 2, r, s)
+ Twiddle(ref x, ref z, i, j);
min = temp < min ? temp : min;
s[i, j] = "Twiddle";
r[i, j] = min;
}
}
}
return min;
}
public static int Copy(ref char[] x, ref char[] z,
int i, int j)
{
z[j] = x[i];
return 1;
}
public static int Replace(ref char[] y, ref char[] z,
int j)
{
z[j] = y[j];
return 2;
}
public static int Delete()
{
return 3;
}
public static int Insert(ref char[] y, ref char[] z,
int j)
{
z[j] = y[j];
return 3;
}
public static int Twiddle(ref char[] x, ref char[] z,
int i, int j)
{
z[j] = x[i + 1];
z[j + 1] = x[i];
return 2;
}
public static int Kill()
{
return 5;
}
}
15.9 字符串拆分
15.9(字符串拆分)某种字符串处理语言允许程序员将一个字符串拆分为两段。由于此操作需要复制字符串,因此要花费n个时间单位来将一个n个字符的字符串拆为两段。假定一个程序员希望将一个20个字符串在第2个、第8个以及第10个字符串后进行拆分(字符串由左至右,从1开始升序编号)。如果她按由左至右的顺序进行拆分,则第一次拆分花费20个时间单位,第二次拆分花费18个时间单位,第三次拆分花费12个时间单位,共花费50个时间单位。但如果她按由右至左的顺序进行拆分,第一次拆分花费20个时间单位,第二次拆分花费10个时间单位,而第三次拆分花费8个时间单位,共花费38个时间单位。还可以按其他顺序,比如,她可以首先在第8个时间单位进行拆分(时间20),接着在左边一段第2个字符处进行拆分(时间8),最后在右边一段第10个字符处进行拆分(时间12),总时间40.
设计算法,对给定的拆分位置,确定最小代价的拆分顺序。
static void Main(string[] args)
{
int[] L = new int[] { 2, 4, 6, 8, 9, 10 };
var text = string.Empty;
for (var i = 0; i < 20; i++)
{
text += 1.ToString();
}
var r = Execute(text, text.Length, L, 0, L.Length - 1);
}
/// <summary>
/// 最小代价字符串拆分
/// </summary>
/// <param name="s"></param>
/// <param name="length"></param>
/// <param name="L"></param>
/// <param name="i"></param>
/// <param name="j"></param>
/// <returns></returns>
public static int Execute(string s, int length,
int[] L, int i, int j)
{
if (i > j)
{
return 0;
}
else if (i == j)
{
return length;
}
int min = int.MaxValue;
for (var k = 0; k < j - i + 1; k++)
{
var r = Execute(s, L[k + i], L, i, k + i - 1) +
Execute(s, 20 - L[k + i], L, k + i + 1, j) +
length;
if (r < min)
{
min = r;
}
}
return min;
}