Day 1.Problem A. 起床困难综合症
100分做法:
把数字看成二进制数。对于初始攻击力,我们将其拆成32位,并求出每一位为0和1时经过所有防御门之后分别得到的数字。然后就是按位贪心了,我们尽量让初始攻击力的高位在经过所有防御门后变成1而不是0,根据这一贪心思想,剩下要做的就是个很简单的数位贪心问题了。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#define MAXN 110000
using namespace std;
typedef long long int LL;
int n,m;
int op[MAXN]; //op[i]=1:AND 2:OR 3:XOR
int t[MAXN];
namespace Biaozhun
{
int digit[100],len=0; //最低位在digit[1]
int ans[100][2]; //ans[i][1]=从低到高第i位,初始取1,最后得到的答案
int sol[100]; //sol保存的是最后得到的答案的最大值
void getDigit(int x)
{
while(x)
{
digit[++len]=x&1;
x>>=1;
}
}
void solve()
{
getDigit(m);
for(int Dig=0;Dig<32;Dig++)
{
int num=0; //初始为0
for(int i=1;i<=n;i++)
{
if(op[i]==1) //AND
num=num&((t[i]&(1<<Dig))?1:0);
else if(op[i]==2) //OR
num=num|((t[i]&(1<<Dig))?1:0);
else //XOR
num=num^((t[i]&(1<<Dig))?1:0);
}
ans[Dig+1][0]=num;
num=1; //初始为1
for(int i=1;i<=n;i++)
{
if(op[i]==1) //AND
num=num&((t[i]&(1<<Dig))?1:0);
else if(op[i]==2) //OR
num=num|((t[i]&(1<<Dig))?1:0);
else //XOR
num=num^((t[i]&(1<<Dig))?1:0);
}
ans[Dig+1][1]=num;
}
bool flag=true; //flag=true表示当前前缀还是和m一样大的
for(int i=32;i>len;i--) sol[i]=ans[i][0];
for(int i=len;i>=1;i--)
{
if(!flag) //初始数字的第i位可以随便填
{
if(ans[i][0]) sol[i]=1;
else if(ans[i][1]) sol[i]=1;
else sol[i]=0;
}
else
{
if(digit[i]==1)
{
if(ans[i][0])
{
flag=false;
sol[i]=1;
}
else if(ans[i][1]) sol[i]=1;
else
{
flag=false;
sol[i]=0;
}
}
else
{
if(ans[i][0])
sol[i]=1;
else
sol[i]=0;
}
}
}
long long int sum=0;
for(int i=32;i>=1;i--)
{
sum<<=1LL;
sum|=(LL)sol[i];
}
printf("%lld\n",sum);
}
}
int main()
{
//freopen("in","r",stdin);
//freopen("out_ceshi","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
char cmd[10];
scanf("%s",cmd);
if(cmd[0]=='A') op[i]=1;
else if(cmd[0]=='O') op[i]=2;
else if(cmd[0]=='X') op[i]=3;
scanf("%d",&t[i]);
}
using namespace Biaozhun;
solve();
return 0;
}
Day 1.Problem B. 魔法森林
15分做法
直接做DFS暴力就行了
50分做法
考虑到一些点里a的范围比较小,因此我们可以枚举初始时携带的A精灵个数limitA,然后二分初始时携带的B精灵个数limitB,BFS来判断是否能走到终点。由于边上的
a
i
的值最多只可能有边数
m
个,因此只需要枚举每种不同的
a
i
来作为
l
i
m
i
t
A
就行了,时间复杂度
O
(
m
l
o
g
(
max
b
i
)
n
)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
int n,m;
inline int read()
{
int tmp=0;
char ch=getchar();
while(ch==' '||ch=='\n') ch=getchar();
while(ch>='0'&&ch<='9') tmp=tmp*10+ch-'0',ch=getchar();
return tmp;
}
namespace BFSSearch
{
const int MAXV=51000;
const int MAXE=210000;
struct edge
{
int u,v,next;
int a,b;
}edges[MAXE];
int head[MAXV],nCount=0;
void AddEdge(int U,int V,int A,int B)
{
edges[++nCount].u=U;
edges[nCount].v=V;
edges[nCount].a=A;
edges[nCount].b=B;
edges[nCount].next=head[U];
head[U]=nCount;
}
int q[MAXE*2],h=0,t=0,S,T;
int vis[MAXV],total=0;
inline bool BFS(int limitA,int limitB)
{
total++;
h=0,t=0;
//memset(vis,false,sizeof(vis));
//cout<<S<<' '<<T<<endl;
q[t++]=1;
vis[1]=total;
while(h<t)
{
int u=q[h++];
if(u==n)
return true;
for(int p=head[u];p!=-1;p=edges[p].next)
{
int v=edges[p].v;
if(vis[v]==total) continue;
if(edges[p].a<=limitA&&edges[p].b<=limitB)
{
q[t++]=v;
vis[v]=total;
}
}
}
return false;
}
int sta[MAXE],top=0;
int minans=1000000000;
void solve()
{
memset(head,-1,sizeof(head));
S=1,T=n;
int maxB=0;
int maxA=0;
for(int i=1;i<=m;i++)
{
int U,V,A,B;
U=read(),V=read(),A=read(),B=read();
AddEdge(U,V,A,B);
AddEdge(V,U,A,B);
sta[++top]=A;
maxA=max(maxA,A); maxB=max(maxB,B);
}
if(n>5000&&m>10000&&maxA>30)
{
printf("-1\n");
return;
}
sort(sta+1,sta+top+1);
top=unique(sta+1,sta+top+1)-sta;
for(int i=1;i<=top;i++)
{
bool flag=false;
int costA=sta[i];
if(!BFS(costA,maxB)) continue;
int lowerBound=0,upperBound=maxB,costB=0;
while(lowerBound<=upperBound)
{
int mid=(lowerBound+upperBound)>>1;
if(BFS(costA,mid))
{
flag=true;
costB=mid;
upperBound=mid-1;
}
else lowerBound=mid+1;
}
if(flag)
minans=min(minans,costA+costB);
}
if(minans==1000000000) minans=-1;
printf("%d\n",minans);
}
}
int main()
{
//freopen("in","r",stdin);
//freopen("out_ceshi","w",stdout);
scanf("%d%d",&n,&m);
using namespace BFSSearch;
solve();
return 0;
}
70分做法
我们可以和50分做法一样枚举
a
i
最大值
l
i
m
i
t
A
,在所有的
a
i
≤
l
i
m
i
t
A
的边里,维护一棵
b
i
之和最小的MST,若在MST加入某条边
i
之后,点1和点
n
连通,那么显然此时
l
i
m
i
t
B
最小可以取
b
i
,因为可以预处理对所有边进行排序,所以这种做法时间复杂度是
O
(
n
m
)
,卡卡常数就能得到70分
//70分做法:Kruscal
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#define MAXN 210000
using namespace std;
struct edge
{
int u,v,a,b;
}edges[MAXN];
int f[MAXN];
int findSet(int x)
{
if(f[x]==x) return f[x];
return f[x]=findSet(f[x]);
}
int read()
{
int ans=0;
char ch=getchar();
while(ch==' '||ch=='\n') ch=getchar();
while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
return ans;
}
int n,m;
int sta[MAXN],top=0;
int minans=1000000000;
bool cmp(edge a,edge b)
{
return a.b<b.b;
}
int Kruscal(int limitA)
{
int tot=0;
for(int i=1;i<=n;i++) f[i]=i;
for(int i=1;i<=m;i++)
{
if(edges[i].a>limitA) continue;
int rootu=findSet(edges[i].u),rootv=findSet(edges[i].v);
if(rootu==rootv) continue;
f[rootu]=rootv;
tot++;
if(findSet(1)==findSet(n)) return edges[i].b;
}
return -1;
}
int main()
{
n=read(),m=read();
for(int i=1;i<=m;i++)
edges[i].u=read(),edges[i].v=read(),edges[i].a=read(),edges[i].b=read(),sta[++top]=edges[i].a;
sort(sta+1,sta+top+1);
sort(edges+1,edges+m+1,cmp);
top=unique(sta+1,sta+top+1)-sta;
for(int i=1;i<=top;i++)
{
int tmp=Kruscal(sta[i]);
if(tmp!=-1) minans=min(minans,sta[i]+tmp);
}
if(minans==1000000000) minans=-1;
printf("%d\n",minans);
return 0;
}
100分做法:
我们可以用link-cut tree来维护此图的一个生成树。初始时,我们对所有边按
a
i
升序排序,往MST里不断放入边,若当前边连接的是两个不同的联通块,则可以直接加入进去。否则若当前边的
b
i
比MST中这条边的两端点连接的路径中
b
i
最大的那条边的
b
i
小的话,则可以加入这条边,并替换掉MST中这条边的两端点连接的路径中
b
i
最大的那条边。若当前点1和点n连通的话,用当前路径上的
max
{
a
i
}
+
max
{
b
i
}
去更新答案
Day 1.Problem C. 消除游戏
第一个测试点
目测可以发现,第一个测试点的矩阵里是一条回文串+一条大质数构成的,手打输出数据就能得到10分
Day 2.Problem A. 动物园
15分做法
对于每个前缀,暴力枚举它的每个前缀是否能满足题目的要求。时间复杂度
O
(
|
S
|
3
)
25分做法
与15分做法类似,对于每个前缀,暴力枚举它的每个前缀是否能满足题目的要求。不同的是使用Hash而不是用暴力来匹配字符串。时间复杂度
O
(
|
S
|
2
)
50分做法
定义
c
n
t
[
i
]
=
前缀i里,
既是前缀又是后缀
(注意没了长度要小于i的限制,也就是说前缀i也可以满足这一条件)的子串个数。
c
n
t
[
i
]
=
1
,假设前缀p是前缀i里最大的,既是前缀又是后缀,长度又
≤
i
2
的子串,那么
n
u
m
[
i
]
=
c
n
t
[
p
]
(前缀p里既是前缀又是后缀的子串个数=[1,p]里是前缀、[i-p+1,i]里是后缀的子串个数)
考虑next指针。next[i]=前缀i里最大的既是前缀又是后缀、且长度
<
i
<script type=”math/tex” id=”MathJax-Element-967″>
≤
i
2
的子串(前缀p)。但是构造一组全部是一种字母的(如aaaa)的字符串,就能使该算法退化到
O
(
|
S
|
2
)
,UOJ中实测50分。
100分做法
与50分做法基本上差不多,但是对于每个前缀i,不是暴力找p,可以发现p指针可以均摊
O
(
1
)
求出,具体看代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#define MAXN 1100000
#define MOD 1000000007
using namespace std;
typedef long long int LL;
char s[MAXN];
int next[MAXN],n;
int cnt[MAXN];
void getnext()
{
next[1]=0;
int p=0;
cnt[1]=1;
for(int i=2;i<=n;i++)
{
while(p&&s[p+1]!=s[i]) p=next[p];
if(s[p+1]==s[i]) p++;
next[i]=p;
cnt[i]=cnt[p]+1;
}
}
LL f[MAXN];
void calc()
{
int p=0;
for(int i=2;i<=n;i++)
{
while(p&&s[p+1]!=s[i]) p=next[p];
if(s[p+1]==s[i]) p++;
while(p&&p*2>i) p=next[p];
f[i]=cnt[p];
}
}
int main()
{
//freopen("in","r",stdin);
//freopen("out_ceshi","w",stdout);
int T;
scanf("%d",&T);
//cout<<"dd"<<endl;
while(T--)
{
memset(f,0,sizeof(f));
scanf("%s",s+1);
n=strlen(s+1);
getnext();
calc();
//for(int i=1;i<=n;i++) cout<<f[i]<<" ";
//cout<<endl;
LL ans=1;
for(int i=1;i<=n;i++)
ans=(ans*(f[i]+1))%MOD;
printf("%lld\n",ans);
}
return 0;
}
Day 2.Problem B. 随机数生成器
10分做法
DFS乱搞
60分做法
问题可以转述为,给棋盘中n+m-1个格子涂色,使得左上角的格子和右下角的格子四连通。
观察发现,要想让得到的序列的字典序尽量小,就应该从1到
n
m
,从小到大填入数字,尽量把小数字都填色。每次给一个格子填色后,会使得该格子左下角和右上角的区域不能填色了。
因此我们可以用二维树状数组来维护每个格子是否能填色。与一般的二维树状数组不同的是,这里需要支持
区间更新
、
单点查询
,因此可以使用差分约束系统,若对左上角为
(
x
1
,
y
1
)
,右下角为
(
x
2
,
y
2
)
的矩阵区间+1,就相当于在BIT中对
(
x
1
,
y
1
)
单点+1,
(
x
2
+
1
,
y
1
)
单点-1,
(
x
2
+
1
,
y
2
+
1
)
单点+1,
(
x
1
,
y
2
+
1
)
单点-1,如下图:
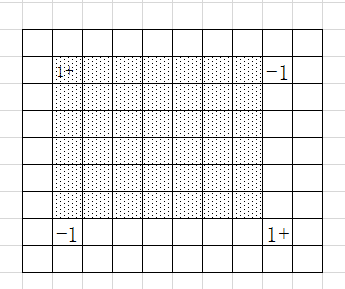
时间复杂度:
O
(
n
m
l
o
g
n
l
o
g
m
)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#define calcpos(x,y) (((x)-1)*m+y)
#define lowbit(x) ((x)&(-(x)))
using namespace std;
typedef long long int LL;
LL lastx,a,b,c,d;
int n,m,Q;
int randnum()
{
LL x=(((a*lastx)%d)*lastx%d+(b*lastx)%d+c)%d;
lastx=x;
return (int)x;
}
namespace Greedy
{
const int MAXN=2100;
int seq[MAXN*MAXN],pos[MAXN*MAXN]; //pos[i]=数字i在随机序列里的下标
int ansseq[MAXN*3],top=0;
bool used[MAXN*MAXN],vislayer[MAXN*3]; //used[(i,j)]=true表示(i,j)这个格子要被经过,vislayer[i]=true表示步数i所走的格子已经确定了
int bit[MAXN][MAXN];
void getRandomSeq(int len)
{
for(int i=1;i<=len;i++) seq[i]=i;
for(int i=1;i<=len;i++)
swap(seq[i],seq[(randnum()%i)+1]);
for(int i=1;i<=Q;i++)
{
int u,v;
scanf("%d%d",&u,&v);
swap(seq[u],seq[v]);
}
for(int i=1;i<=len;i++) pos[seq[i]]=i;
}
inline bool inMap(int x,int y)
{
if(x<1||x>n||y<1||y>m) return false;
return true;
}
inline void update(int x,int y,int val)
{
while(x<=n)
{
int tmpy=y;
while(tmpy<=m)
{
bit[x][tmpy]+=val;
tmpy+=lowbit(tmpy);
}
x+=lowbit(x);
}
}
int query(int x,int y) //false表示(x,y)可以用
{
int ans=0;
while(x)
{
int tmpy=y;
while(tmpy)
{
ans+=bit[x][tmpy];
tmpy-=lowbit(tmpy);
}
x-=lowbit(x);
}
return ans;
}
void Update(int zsx,int zsy,int yxx,int yxy)
{
yxx++,yxy++;
update(yxx,yxy,-1);
update(zsx,zsy,-1);
update(yxx,zsy,1);
update(zsx,yxy,1);
}
int Query(int zsx,int zsy,int yxx,int yxy)
{
zsx++,zsy++,yxx++,yxy++;
return query(yxx,yxy)+query(zsx-1,zsy-1)-query(yxx,zsy-1)-query(zsx-1,yxy);
}
void solve()
{
getRandomSeq(n*m);
int R=n*m;
ansseq[++top]=seq[1];
if(n!=1&&m!=1) ansseq[++top]=seq[R];
int nowX,nowY;
nowX=1,nowY=1;
Update(nowX+1,1,n,nowY-1);
Update(1,nowY+1,nowX-1,m);
nowX=n,nowY=m;
Update(nowX+1,1,n,nowY-1);
Update(1,nowY+1,nowX-1,m);
for(int i=1;i<=R;i++)
{
if(i==seq[1]||i==seq[R]) continue;
int nowpos=pos[i];
if(nowpos%m)
{
nowX=nowpos/m+1;
nowY=nowpos%m;
}
else
{
nowX=nowpos/m;
nowY=m;
}
//cout<<nowX<<" "<<nowY<<endl;
//cout<<Query(nowX,nowY,nowX,nowY)<<" dd: "<<i<<endl;
if(query(nowX,nowY)) continue;
ansseq[++top]=i;
if(top==n+m-1) break;
Update(nowX+1,1,n,nowY-1);
Update(1,nowY+1,nowX-1,m);
}
sort(ansseq+1,ansseq+top+1);
for(int i=1;i<=top;i++)
printf("%d ",ansseq[i]);
printf("\n");
}
}
int main()
{
scanf("%lld%lld%lld%lld%lld",&lastx,&a,&b,&c,&d);
scanf("%d%d%d",&n,&m,&Q);
using namespace Greedy;
solve();
return 0;
}
100分做法
非常搞笑的是,此题满分做法比70分做法好写很多!
思路基本上和70分做法差不多,只不过维护每个点是否可以染色,从二维树状数组维护,变成了暴力维护。由于每行可以染色的区域永远是一个连续的区间,因此我们只需要记录每一行
i
所对应的可行染色区域
[
L
i
,
R
i
]
即可,那么这样的话,每次查询某个格子是否可以染色是
O
(
1
)
的,而更新
L
[
]
,
R
[
]
数组则是
O
(
n
)
的,此题里,查询次数是
O
(
n
m
)
,更新次数则是
O
(
n
+
m
)
,因此非常神奇的一幕发生了:这种看上去非常sb的暴力,复杂度仅有
O
(
n
(
n
+
m
)
)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#define calcpos(x,y) (((x)-1)*m+y)
#define lowbit(x) ((x)&(-(x)))
using namespace std;
typedef long long int LL;
LL lastx,a,b,c,d;
int n,m,Q;
int randnum()
{
LL x=((a*lastx+b)*lastx+c)%d;
lastx=x;
return (int)x;
}
namespace Greedy
{
const int MAXN=5100;
int seq[MAXN*MAXN],pos[MAXN*MAXN]; //pos[i]=数字i在随机序列里的下标
int ansseq[MAXN*3],top=0;
int L[MAXN],R[MAXN];
void getRandomSeq(int len)
{
for(int i=1;i<=len;i++) seq[i]=i;
for(int i=1;i<=len;i++)
swap(seq[i],seq[(randnum()%i)+1]);
for(int i=1;i<=Q;i++)
{
int u,v;
scanf("%d%d",&u,&v);
swap(seq[u],seq[v]);
}
for(int i=1;i<=len;i++) pos[seq[i]]=i;
}
void solve()
{
getRandomSeq(n*m);
int End=n*m;
ansseq[++top]=seq[1];
if(n!=1&&m!=1) ansseq[++top]=seq[End];
for(int i=1;i<=n;i++) L[i]=1,R[i]=m;
for(int i=1;i<=End;i++)
{
int nowX,nowY;
if(i==seq[1]||i==seq[End]) continue;
int nowpos=pos[i];
if(nowpos%m)
{
nowX=nowpos/m+1;
nowY=nowpos%m;
}
else
{
nowX=nowpos/m;
nowY=m;
}
//cout<<"nowX: "<<nowX<<" nowY: "<<nowY<<" L: "<<L[nowX]<<" R: "<<R[nowX]<<endl;
if(nowY<L[nowX]||nowY>R[nowX]) continue;
ansseq[++top]=i;
if(top==n+m-1) break;
for(int i=1;i<=nowX-1;i++)
R[i]=min(R[i],nowY);
for(int i=nowX+1;i<=n;i++)
L[i]=max(L[i],nowY);
}
sort(ansseq+1,ansseq+top+1);
for(int i=1;i<=top;i++)
printf("%d ",ansseq[i]);
printf("\n");
}
}
int main()
{
scanf("%lld%lld%lld%lld%lld",&lastx,&a,&b,&c,&d);
scanf("%d%d%d",&n,&m,&Q);
using namespace Greedy;
solve();
return 0;
}
Day 2.Problem C. 购票
30分做法
暴力地求出树中每一层的结点是哪些。然后我们按照树的层数为阶段做DP,
f
[
i
]
=
点i到根节点所需最少费用。那么
f
[
i
]
可以转移到
f
[
j
]
,当且仅当j在i的子树里。我们在dp f[i]时,直接沿着父亲指针往上爬来枚举j即可
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <vector>
#define MAXN 210000
using namespace std;
typedef long long int LL;
vector<int>listOfDep[MAXN];
int n,T;
pair<int,int>q[MAXN*2];
LL P[MAXN],Q[MAXN],dis[MAXN];
struct edge
{
int u,v,next;
LL w;
}edges[MAXN];
int head[MAXN],nCount=0;
void AddEdge(int U,int V,LL W)
{
edges[++nCount].u=U;
edges[nCount].v=V;
edges[nCount].w=W;
edges[nCount].next=head[U];
head[U]=nCount;
}
int fa[MAXN];
int maxDep=0;
LL Depth[MAXN]; //Depth[i]=i到根节点的距离
LL f[MAXN];
void BFS()
{
int h=0,t=1;
q[h]=make_pair(1,1);
listOfDep[1].push_back(1);
Depth[1]=0;
while(h<t)
{
int u=q[h].first,dep=q[h++].second;
maxDep=max(maxDep,dep);
for(int p=head[u];p!=-1;p=edges[p].next)
{
int v=edges[p].v;
q[t++]=make_pair(v,dep+1);
listOfDep[dep+1].push_back(v);
Depth[v]=Depth[u]+edges[p].w;
}
}
}
void DP()
{
f[1]=0;
for(int depth=2;depth<=maxDep;depth++)
{
for(int id=0;id<listOfDep[depth].size();id++)
{
int i=listOfDep[depth][id];
for(int j=fa[i];j;j=fa[j])
{
if(Depth[i]-Depth[j]>dis[i]) break;
f[i]=min(f[i],f[j]+P[i]*(Depth[i]-Depth[j])+Q[i]);
}
}
}
}
void solve()
{
memset(head,-1,sizeof(head));
memset(f,0x3f,sizeof(f));
for(int i=2;i<=n;i++)
{
LL w;
scanf("%d%lld%lld%lld%lld",&fa[i],&w,&P[i],&Q[i],&dis[i]);
AddEdge(fa[i],i,w);
}
BFS();
DP();
for(int i=2;i<=n;i++) printf("%lld\n",f[i]);
}
int main()
{
scanf("%d%d",&n,&T);
solve();
return 0;
}