博客

算法思想

决策树（decision tree）是一个树结构（

可以是二叉树或非二叉树

）。

其每个非叶节点表示一个

特征属性

上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个

类别

。

使用决策树进行决策的过程就是从

根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

总结来说：

决策树模型核心是下面几部分：

• 
  结点和有向边组成
  
• 
  结点有内部结点和叶结点俩种类型
  
• 
  内部结点表示一个特征，叶节点表示一个类
  

决策树表示如下：

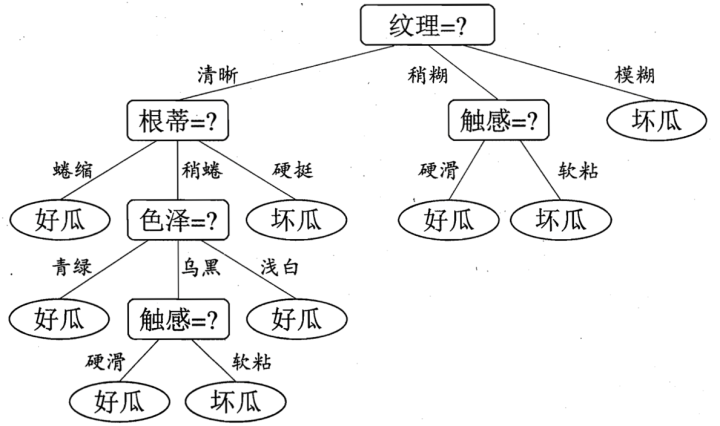
（摘自周志华老师西瓜书）

决策树代表实例属性值约束的合取的析取式。从树根到树叶的每一条路径对应一组属性测试的合取，树本身对应这些合取的析取。理解这个式子，比如上图的决策树对应表达式为：

（（纹理=清晰）

(根蒂=蜷缩)）

（（纹理=清晰）

(根蒂=稍蜷)

（色泽=乌黑）

（触感=硬滑））

……….(纹理=模糊)

决策实例

假如我现在告诉你，我买了一个西瓜，它的特点是纹理是清晰，根蒂是硬挺的瓜，你来给我判断一下是好瓜还是坏瓜，恰好，你构建了一颗决策树，告诉他，没问题，我马上告诉你是好瓜，还是坏瓜？

判断步骤如下：

根据纹理特征，已知是清晰，那么走下面这条路，红色标记：

好的，现在咋们到了第二层了，这个时候，由决策树图，我们看到，我们需要知道根蒂的特征是什么了？很好，他也告诉我了，是硬挺，于是，我们继续走，如下面蓝色所示：

此时，我们到达叶子结点了，根据上面总结的点，可知，叶子结点代表一种类别，我们从如上决策树中，

可以知道，这是一个坏瓜！

于是我们可以很牛的告诉他，你买的这个纹理清晰，根蒂硬挺的瓜是坏瓜，orz！

回归源头

根据上面例子，非常容易直观的得到了一个实例的类别判断，只要你告诉我各个特征的具体值，

决策树的判定过程就相当于树中从根结点到某一个叶子结点的遍历。每一步如何遍历是由数据各个特征的具体特征属性决定。

好的，可能有人要问了，说了这么多，给你训练数据，你的决策树是怎么构建的呢？没有树，谈何遍历，谈何分类？

于是构建决策树也就成为了最重要的工作！

比如，给我下面训练数据，我如何构建出决策树

我们可以从上面决策树看出，每一次子结点的产生，是由于我在当前层数选择了不同的特征来作为我的分裂因素造成的。比如下图用红色三角形表示选择的特征：

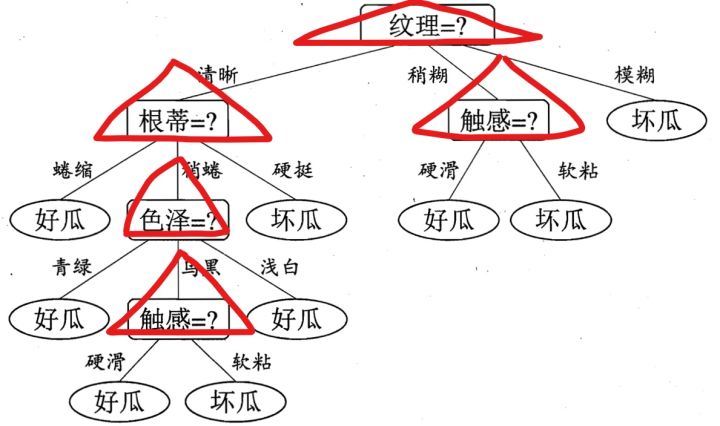
每一层选择了指定的特征之后，我们就可以继续由该特征的不同属性值进行划分，依次一直到叶子结点。

看起来一切很顺利！但是细心的小伙伴可能会问了，为什么在第一次选择特征分裂的时候，不选择触感呢？而是选择纹理，比如如下：

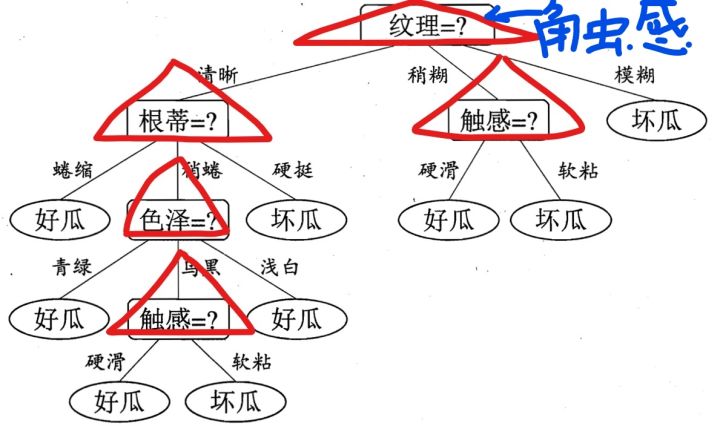
不换成触感，或者其它特征为什么也不行呢？为什么选择的是纹理，

这是以什么标准来选择特征的？

这就是我们要说的决策树的关键步骤是分裂属性。

所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支，其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。

而判断“纯”的方法不同引出了我们的ID3算法，C4.5算法以及CART算法，这些后面会详细介绍！