凸透镜成像原理

1.焦点与焦距：

2.基本原理：

u 为物距， f 为焦距，v 为像距，则有：

3.成像特点

（1）物距 < f

（2）f < 物距 < 2f

（3）物距 > 2f

摄像原理

照相机中 焦距f<像距<2f 才能成像

针孔相机成像模型：

涉及到的

四个坐标系

：

（1）世界坐标系：世界坐标系下的点P，即生活中真实的一点；还用来描述相机的位置

（2）相机坐标系：以相机的光心为原点

（3）图像坐标系：以成像平面的中点为原点

（4）像素坐标系：uv像素坐标系，原点在图像左上角，单位是像素；每一像素的坐标（u,v）分别是该像素在数组中的行数和列数

坐标系之间的

变换

：（也是DIBR原理）

（1）像素坐标系O0-u,v与图像坐标系O1-x,y：

像素坐标系中（u,v）只代表行数和列数，像素在图像中的位置没有用物理单位表示出来，所以建立了以物理单位表示的图像坐标系O1-x,y；

u轴与x轴平行，v轴与y轴平行，图像坐标系原点O1在像素坐标系中坐标为（u0,v0），dx和dy分别表示一个像素在x轴和y轴上的物理尺寸；

对于图像坐标系下的一点（x,y），其在像素坐标系下的坐标为（u,v），则有：

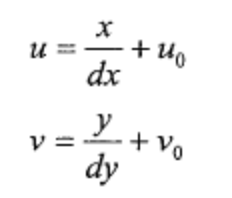
齐次坐标与矩阵形式表示为：

逆关系表示为：

（2）相机坐标系与图像坐标系

令投影中心位于一个欧式坐标系的原点，而平面Z = f被称为图像平面或聚焦平面。

相机坐标系C-X,Y,Z下的一点X=（X，Y，Z）映射到图像平面上图像坐标系中的点x，该点是连接点X与投影中心的直线与图像平面的交点。

根据相似三角形可知，点X = (X, Y, Z)被映射到图像坐标系中的点x = (fX/Z, fY/Z)，则中心投影为：

矩阵形式：

若点X用 4 维齐次矢量 (X,Y,Z,1)T表示；图像点x被表示成 3 维齐次矢量的形式；P 表示 3 × 4 齐次摄像机投影矩阵，则有：

注意这里的Z就是像素点的深度。

PS：

当相机坐标系和图像坐标系z轴不重合时：

则有：

投影

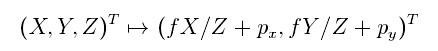
矩阵形式

即

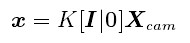
矩阵K为相机的标定矩阵，相机的内参。

有些相机像素不是正方形，此类相机的标定矩阵K一般为

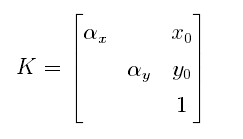
（3）世界坐标系与相机坐标系

通常空间点采用不同的欧式坐标系表示，称为世界坐标系。世界坐标系和摄像机坐标系之间通过旋转和平移相联系

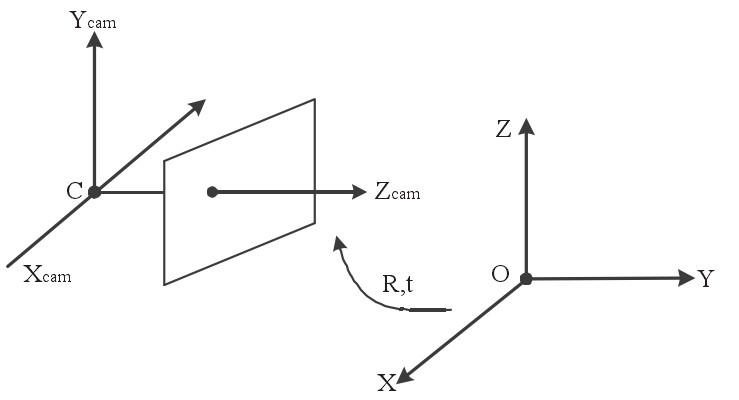
R-旋转参数，3 × 3正交旋转矩阵    t-平移参数，三维平移向量     表示相机的外参

世界坐标系下的点X到相机坐标系下的点Xcam可以表示为Xcam = RX+t

世界坐标系下的点到像素坐标系的转换：

Zc表示的像素点的深度值

ax, ay分别是图像水平轴和垂直轴的尺度因子。K的参数中只包含焦距、主点坐标等只由相机的内部结构决定，因此称 K 为内部参数矩阵，ax, ay , u0, v0叫做内部参数。M1中包含的旋转矩阵和平移向量是由相机坐标系相对于世界坐标系的位置决定的，因此称M1为相机的外部参数矩阵，R和t叫做外部参数，M 叫投影矩阵。

相机标定就是确定相机的内部参数和外部参数。

立体视觉

投影视觉是多对一的关系，投影线上的任何一点都对应于同一个像素点

当有两个相机时，就可以消除这种多对一，从而确定第三维坐标Z的值，即深度信息

这是利用了

视差

。

视差

定义：从具有一定间隔的两个点上观察同一目标时产生的方向上的差异。

数据建模：假设两个相机的内部参数（焦距、镜头等）一致，两个相机x轴方向一致，像平面重合，如下图所示：

对于空间中的一点P =（X，Y，Z）

Tx一般指

基线

，根据三角形相似原理可知，P点在左右相机的像平面坐标为

左相机像平面投影坐标

右相机像平面投影坐标

视差d = Xl – Xr = fTx/Z

Z表示深度。