博客

代价/损失函数cost/lose function将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数，一般用在回归问题以及分类问题:

回归问题(y=kx+b)一般为:

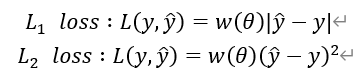
分类问题(0-1问题)一般为:此外还有更多的二元类的损失函数

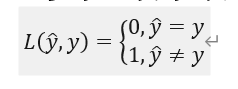
为什么要使用梯度下降方法去寻找最小值:因为在上面得回归问题上，如果参数够多(维度)得情况下无法做到快速寻找到最小值。

1.初始化数据

2.通过步长改变参数获取偏导

我们可以由一个未知参数x演化成多项位置参数x0-xn即n+1项线性问题，同时我们也可以使用矩阵相乘合成该表达式(多元线性回归):

在这里我们需要保持样本保持在相似规模上，就好比在区间[0-1000]与[0-10]之间的步长定义，我们可以使用相似等比定制(数据归一化)。

数据预处理之中心化（零均值化）与标准化（归一化）

https://blog.csdn.net/GoodShot/article/details/80373372

意义


:

数据中心化和标准化在回归分析中是取消由于量纲不同、自身变异或者数值相差较大所引起的误差。

原理


:

数据标准化：(指数值-均值)/标准差

数据中心化：指数值-均值

目的:

通过中心化和标准化处理，得到均值为0，标准差为1的服从标准正态分布的数据。

学习率的技巧:如何选择学习率:首先通过的数据中心化标准化之后，将步长根据均值进行从大到小的改变。

使用正规方程寻找最优解


:

使用微积分求出最小化代价函数J的参数值。通过齐次方程组即可求出。

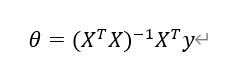
使用梯度下降与正规方程之间区别为1.是否需要选择学习率2.是否需要多次迭代3.当计算量大时n是否会计算量爆炸。在n=10^4的结点附近可以考虑是否梯度下降与正规方程之间的选择。

当遇见奇异矩阵/退化矩阵/不可逆矩阵的时候我们该如何使用正规方程:pinv与inv之间的关系(如遇到两个重合的特征值-面积之间的换算+特征值过多但数据量过少m<=n——这种情况我们会减少特征值的数量或者正规化)

在分类问题情况下，我们需要引出PT NT PF NF等等名词，因为分类问题中不能使用线性回归这种办法去解决部分边缘数据(过拟合)

Logistic回归:logistic function = sigmoid function

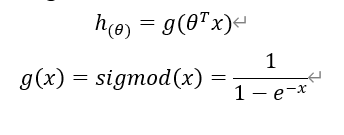
容易梯度爆炸和梯度消失、处处可导、导数可以由自己推出

ReLu


x


=

max⁡

(0,


x


)

更适合梯度下降与反向传播

在使用logistic回归决策的时候，我们可以使用:

损失函数:需要符合凸优化问题(y只能为0/1)

一对多分类器:其实就是多个二分类组成的多分类器，然后通过

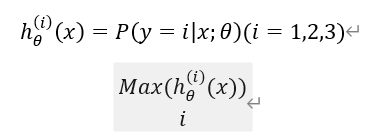
如何减少过拟合的现象:1.人工检查变量清单并判别变量的取舍，也就是减少特征变量2.保留特征值，并且实现特征值正则化

什么是正则化:正则化可以翻译为规则化，在模型加入某些规则，加入先验，缩小解空间，减小求出错误解的可能性，对于代价函数来说，加入对模型过拟合的惩罚。

对梯度下降做正则化:

其中的a/m是一个比1稍小的数。

对正规方程做正则化:

这里面的矩阵第一行是0且其余斜对角为1的矩阵。并且这个矩阵为[n+1][n+1]。

神经网络

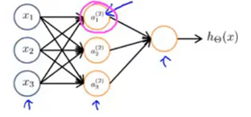
通过神经网络向前传播模型我们可以将矩阵运算的结果作为sigmod的参数。

使用向量表示:

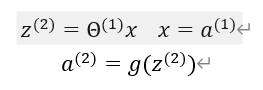
在下一层中:

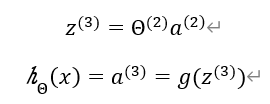
使用一个最简单的例子:AND并且使用sigmod实现

神经网络在多层情况下，第一层担负最简单的运算，第二层承担复杂运算等，依次往后，最后使用代价函数计算值。

使用神经网络进行分类时，我们一般使用矩阵表示(矩阵的m由类别决定)，并且代价函数为:

逻辑回归代价函数

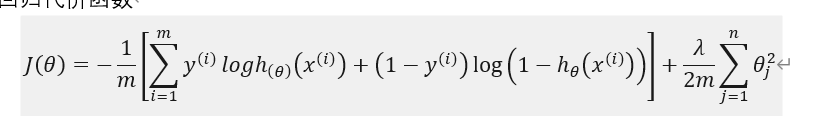
神经网络代价函数

后面的正则化参数是需要联动每层神经网络的神经元数量

我自己对使用神经网络处理数字识别算法的理解，本质就是训练出正确的权重和偏置。使用input-CNN1-CNN2-output处理数字识别，首先将文字写分成若干小块，并且使用权值w(有正有负)，需要进行吻合比对，有则为大，无则为小。在处理CNN1较为简单的处理之后，开始对CNN2进行复杂运算。

内部的激活函数基本就是sigmod函数了，偏置加权值需要额外讨论。而反向传播则是向前对权重和偏置就行调整。以下是使用微积分进行理解反向传播的原理。

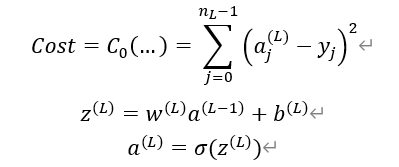
并且使用链式法则求偏导

对偏置求偏导

PCA算法

https://zhuanlan.zhihu.com/p/77151308

PCA：希望投影后的投影值尽可能分散，因为如果重叠就会有样本消失。当然这个也可以从熵的角度进行理解，熵越大所含信息越多。

协方差：在一维空间中我们可以用方差来表示数据的分散程度。而对于高维数据，我们用协方差进行约束，协方差可以表示两个变量的相关性。为了让两个变量尽可能表示更多的原始信息，我们希望它们之间不存在线性相关性，因为相关性意味着两个变量不是完全独立，必然存在重复表示的信息。

https://blog.csdn.net/xiao_lxl/article/details/72730000

Opencv人脸识别方法

FisherFace是基于线性判别分析(LDA)实现的.给定数据集,设法将样本投影在一条直线上，使得同类样本的投影点尽可能地接近，不同的样本地投影点尽可能地远离。对于新样本只需要在该轴投影即可分辨其类别。

LDA与PCA相同之处：降维的时候，两者都使用了矩阵的特征分解思想。两者都假设数据符合高斯分布。

不同之处：LDA是有监督的降维方法，PCA为无监督的。LDA只能将维度降低至k-1维，PCA不受限制。LDA除了可降维还可以用于分类，PCA只能用于降维。从数学角度看，PCA选择样本点投影具有最大方差的方向，LDA选择分类性能最好的投影方向。

Dilb人脸检测方法

LBP特征、Haar特征、Hog特征

LBP(局部二值模式)使用的softmax函数

res(x)=


1 x≥i


0 x<i

描述图像局部纹理特征的算子，进行特征提取，提取图像的局部纹理特征。

Haar特征采用输入图像的矩形特征。在既定有限的数据情况下，通过基于特征值的检测既定区域检测特征，相比较于使用像素系统快很多。

https://blog.csdn.net/kangshuaibing/article/details/84023440

方向梯度直方图（Histogram of Oriented Gradient, HOG），计算一块区域内的所有像素处的梯度信息，即突变的方向和大小，然后对360度进行划分，得到多个bin，统计该区域内的所有像素所在的bin，就得到了一个histogram。

水平模板：[-1,0,1]，水平方向以水平向右为正方向

竖直模板：[1, 0,-1]^T，竖直方向以竖直向上为正方向

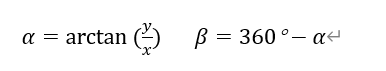
在实现人脸识别的前提下需要实现人脸检测，在Hog特征值的方案下，我们可以使用NMS （Non-Maximum Suppression）非极大值抑制方案消除重叠多余的检出人脸。

https://www.jianshu.com/p/d452b5615850