之前我们说过了一阶系统的单位响应,在生活中也有着二阶系统的单位响应,比如牛顿第二定律
中a就是位移x的二阶导数,还比如弹簧阻尼系统等等。
之前我们提到了拉普拉斯变换的微分性质和积分性质,所以对于二阶的导数我们也能轻易的给出其拉普拉斯变换后的式子,在此我就不过多赘述了,根据原来的极点定理我们就能得到使其稳定的点,简单来说,二阶系统和一阶系统的差别不大,主要是计算,接下来说一下比例控制器。
之前的文章提到了比例控制和稳态误差,稳态误差
以及其的产生原因我在上篇文章都有着具体描述,接下来主要是介绍一下他的解决办法。
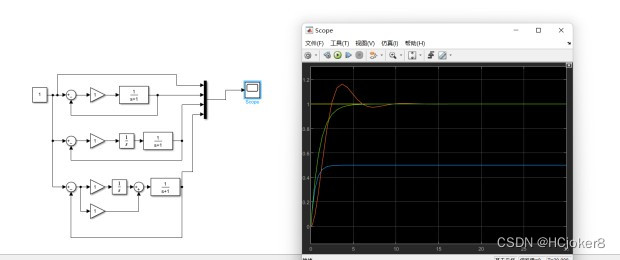
如图所示是一个在sumilink下创建的系统,重上至下分别对应了图中的蓝线、橙线和绿线,我们之前提到了比例控制为纯在常熟Kp,使得单位响应是原来的Kp倍,但是会出现稳态误差,于是,我们使得Kp
C(s),再次计算得出
。于是,我们在这里使目标值为1,分别给出了原比例控制(蓝色线),改进后的比例控制(橙色线)和二者结合(绿色线),可以很清楚的看到蓝色部分改变快,但纯在稳态误差,橙色部分变化较慢但是会摇摆直至趋于目标值,而绿色则是结合了前二者的优点。所以,我们在设置一个控制器的时候,可以根据需求来指定特殊的控制器,从而达到效果
版权声明:本文为HCjoker8原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。