一、计算机硬件的基本组成
未解决早期计算机不会自动执行后面指令的问题,冯*诺依曼等人提出
存储程序
的概念:将指令以二进制代码的形式
事先输入计算机的主存储器,然后按其在存储器中的首地址执行程序的第一条指令,以后就按程序的规定顺序执行其他指令,直到程序执行结束。
1、早期的冯诺依曼机:
以运算器为中心,削弱了运算器的计算能力。
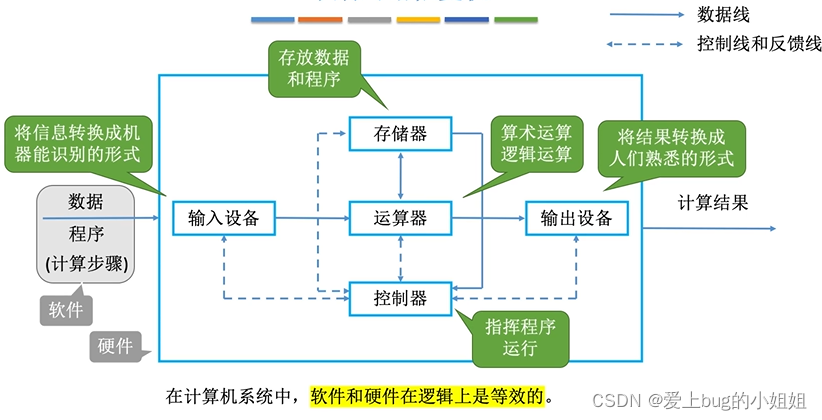
带箭头的实线代表数据线(在两部件间进行数据交流),虚线表示控制线和反馈线(由控制器下达控制命令)
通过上图,我们可以总结出冯诺依曼机的几个特点:
- 计算机由五大部件组成:运算器、存储器、控制器、I/O设备(输入、输出设备)
- 指令和数据皆采用二进制来表示
- 存储程序
为什么说软件和硬件在逻辑上是等效的呢?
比如说乘法运算,我们可以设计一个硬件专门执行乘法运算,也可以通过累加的程序进行运算,最终所得到的结果是一样的,只是程序累加的方式明显累赘了很多。
2、 现代计算机:
以存储器为中心
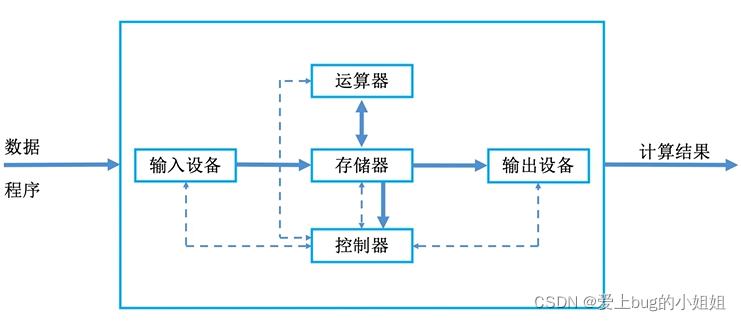
其中,运算器和控制器可以统称为CPU,CPU+主存储器就称为了主机。

要注意主存和辅存的区别:主存是位于主机中的,而辅存是属于I/O设备里的。我们平时手机上的APP就是装在辅存上的,只有当app要启动的时候,才会把相关数据、程序文件读到主存里。
3、对基本部件的细分理解:
(1)主存储器
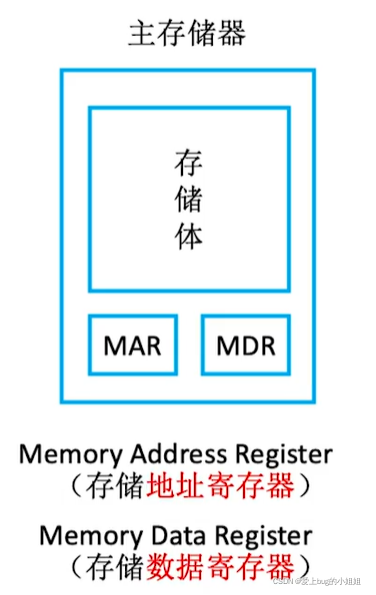
主存储器包括存储体和MAR、MDR。
存储体中是一个仓库,里面有各种各样的架子,按一定顺序编号,存储的每一个数据都有属于自己唯一的地址编号。

MAR中的地址上都对应着一个存储单元,存储单元存储着存储字,存储字是一串二进制代码(数据)。
MAR的位数反映了存储单元的个数,一个地址对应一个存储单元。
MDR的位数和存储字长一样。
两种操作:
-
读——其他部件需要读取主存中的内容
该部件将需要数据的地址给MAR,MAR再传到存储体,取出数据交由MDR,交给该部件。 -
写——其他部件需要将内容保存进主存
该部件将需要保存的数据地址传给MAR,数据传给MDR,经主存内部操作后,即可将数据存入指定地址内。
注意:有的资料也会将MAR、MDR归到CPU中
(2)运算器
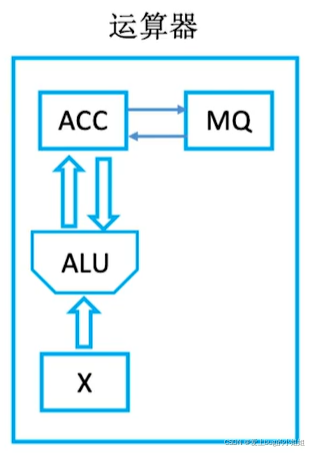
ACC(累加器):存放操作数/运算结果
MQ(乘商寄存器):在乘、除法运算时,用于存放操作数/运算结果
X(通用寄存器):存放操作数
ALU(算术逻辑单元):实现算术运算/逻辑运算
(3)控制器
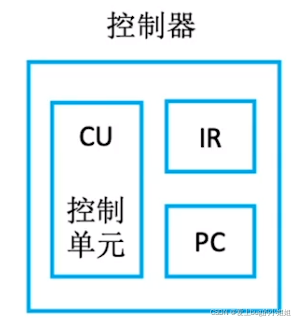
CU(控制单元):分析指令(分析操作码),给出控制信号
IR(指令寄存器):存放当前执行的指令,拆解为操作码和地址码
PC (程序计数器):存放下一条指令地址,自动加1
(例子)指令周期
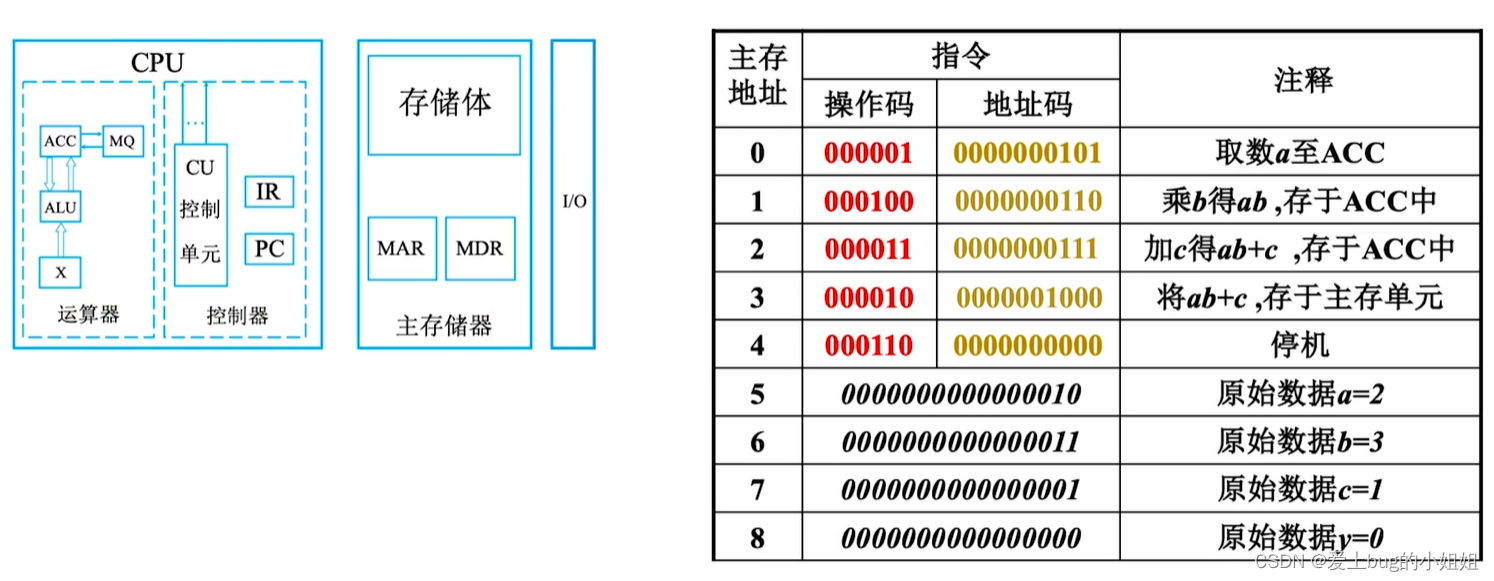
公共周期:(取指,分析)
- (PC)->MAR
- MAR经过存储体将数据通过MDR返回:(MDR)->IR
- OP(IR)->CU
- 根据所得不同的操作码,才决定最终地址码应该送往何处
二、数制及其转换
基数:r进制的基数是r,比如十进制的基数是10——0~9共十个数
位权:每一位代表的权值,比如十进制——个十百千万。。。
1、各进制转换为十进制:
方法:将各位上的数字乘上位权之和
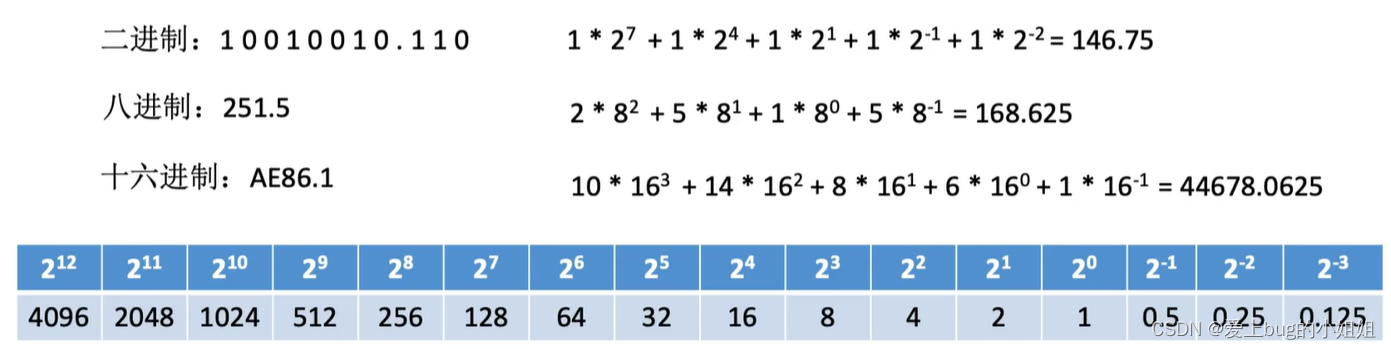
2、二进制和八进制、十六进制的相互转换
(1)二进制转换为八进制
方法:将二进制数以小数点为界限,向两边,
三位为一组
,不够则补0,最后将每一组算出其十进制下的值。
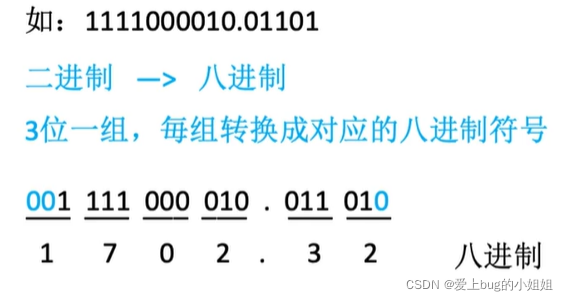
(2)二进制转换为十六进制
方法:将二进制数以小数点为界限,向两边,
四位为一组
,不够则补0,最后将每一组算出其十进制下的值。

(3)八进制转换为二进制
方法:将八进制数每一位对应展开为
三位
二进制的数

(4)十六进制转换为二进制
方法:将十六进制数每一位对应展开为
四位
二进制的数

3、十进制转换为二进制
十进制转换为其他进制,方法类似
(1)整数部分
除基求余法:
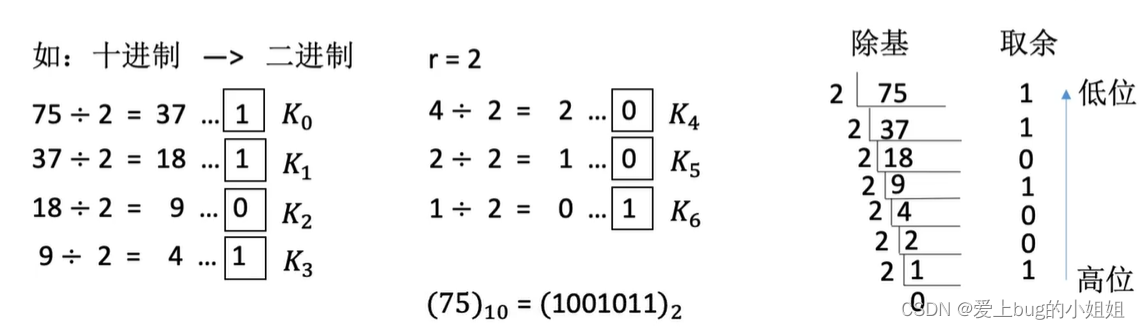
(2)小数部分
乘基取整法:

(3)十进制转为二进制(拼凑法)
比如十进制260.75转换为二进制
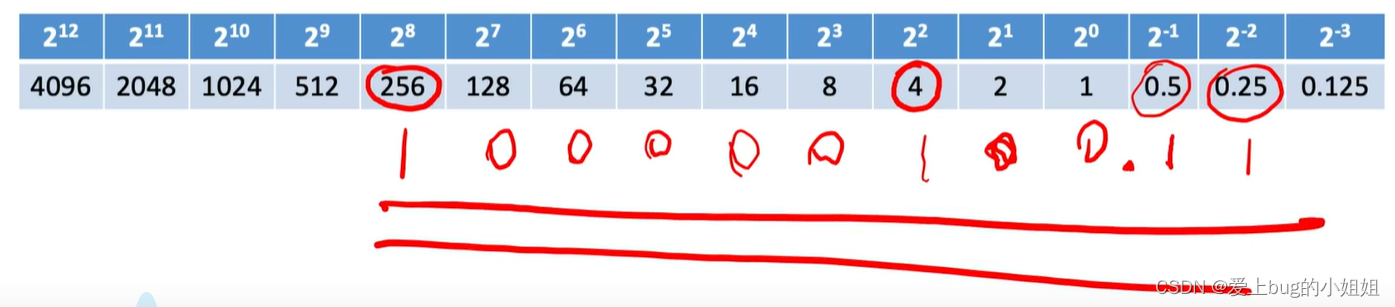
(4)总结:
其实数制转换最主要的还是二进制和十进制间的转换,二进制转换为十进制的方法是各进制转换为十进制的通用方法,而二进制可以非常方便的转换为八进制和十六进制,所以如果需要将十进制转换为八进制或者十六进制的时候,我们可以先将十进制转换为二进制,再将二进制转换为对应的八进制或者十六进制。
三、定点数
1、定点数的表示
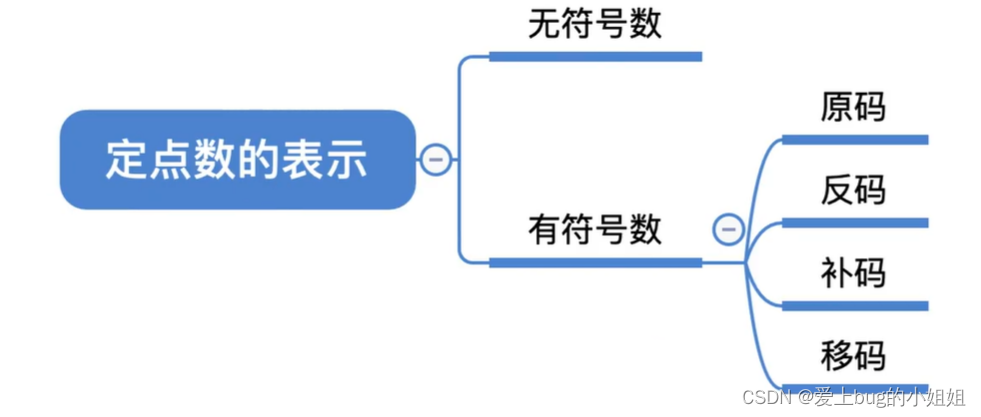
(1)无符号数(unsigned):
整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值
无符号unsigned只能修饰int、long等整形变量,不能修饰小数。

(2)有符号数:
定点整数、定点小数
设置最高位为符号位0为正1为负!
i.原码
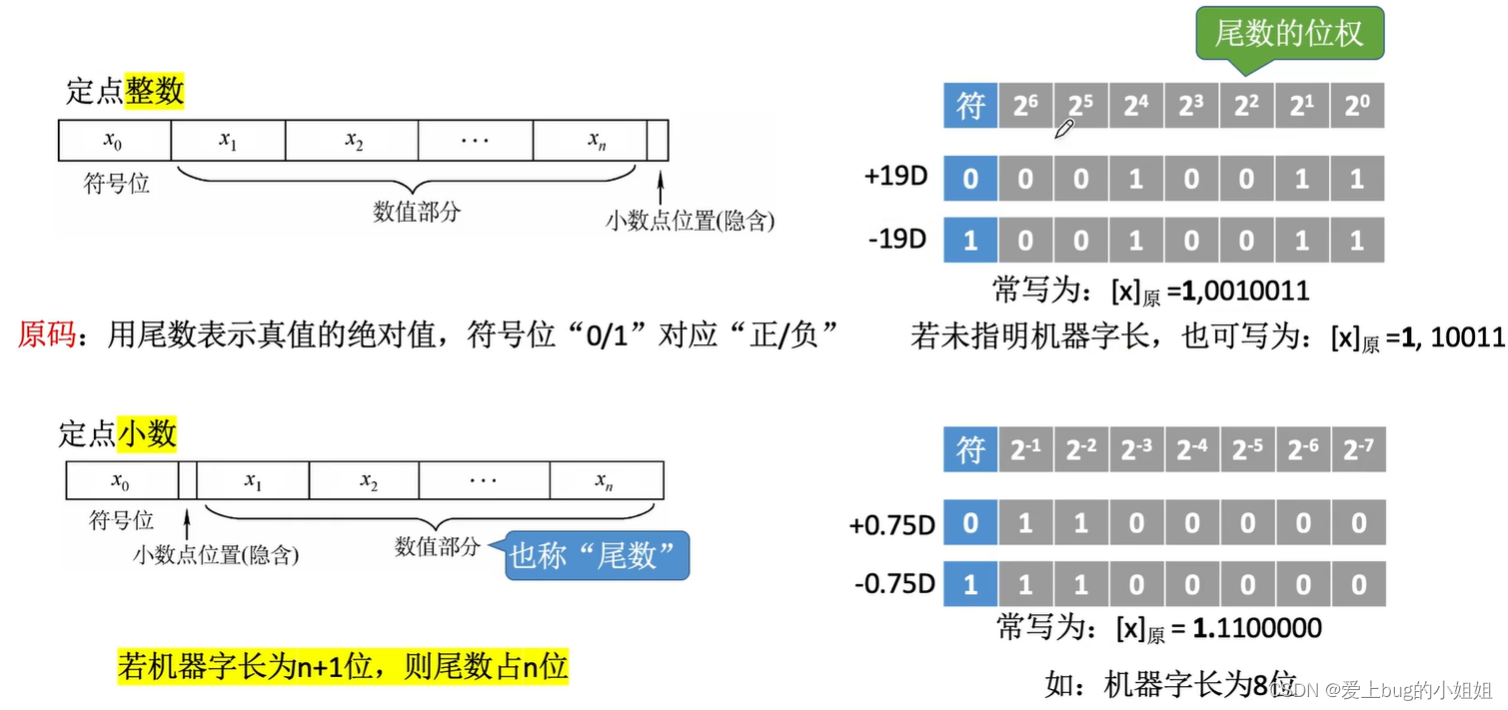
这里特别要注意的是最高位如果是1的时候,要时刻谨记它是符号位,不是数值,尤其是定点小数的原码表示的时候!!!
比如原码:1.1000表示的真值是-0.5,而不是1.5,更不是-1.5
原码表示真值0有两种表示形式+0、-0
ii.反码
一些课本上的描述确实挺复杂的,所以这里就不采用课本的讲法了。
反码只是原码转换为补码的一个中间状态,实际上反码并没有什么太大的用途,计算机不会采用反码进行加减乘除各种运算。
其实在反码这一块只需要记住两句话,即可:
- 正数的反码和原码一样
- 负数的反码:将原码各位取反,符号位除外
注意:反码对0的表示也有+0、-0两种表示方法。
ii.补码
- 正数的补码和原码一样
- 负数的补码=反码末位+1=除符号位,原码各位取反+1
注意:反码对0的表示只有0一种表示方法。
补码转原码:各位取反末位+1,符号位除外
iii.移码
移码是在补码的基础上将符号位取反,但是有一点需要注意的是:移码只能用于表示整数。
(3)原码、补码、移码的作用
i.原码计算的缺点

如果是00001110和10001110是两真值(无符号位)相加是可以得到正确结果的,可以原码中最高位表示符号位。。。
正数的原码的想加是没问题的,可是一正一负,就会出现计算结果错误了,但是这时候可采用另一种方法,将一正一负想加转换为减法运算即可得到正确结果,然而这却涉及到一个高成本的问题,毕竟减法器比加法器可是要复杂多了。
这时候,就有人灵光一闪:可以将减法运算转换成加法运算吗?该怎么转换??
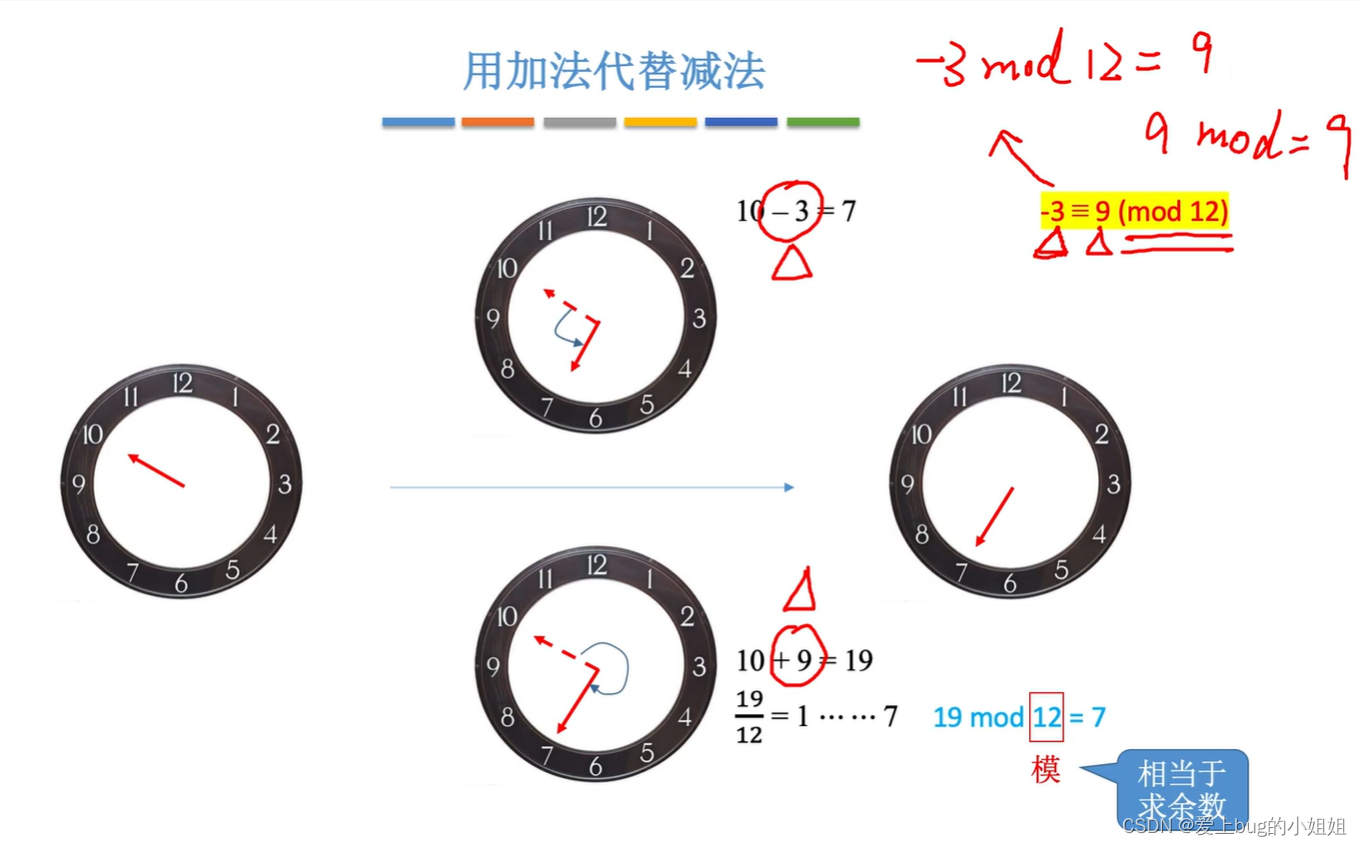
顺时针方向为加,逆时针方向为减
mod方法:对于两个数只要两绝对值相加等于模,则说明两个数等价。
比如:
|A|+|B|=C,则说明AmodC=B,BmodC=A
上面时钟的例题同样也是如此,
|-3|+9=12,则-3mod12=9,9mod12=9
这时候说明-3和9是等价的,即当前数加上9和减去3是等效的,也就是说明此时的减3可以转换为加9,减法运算也就转换为加法运算了。
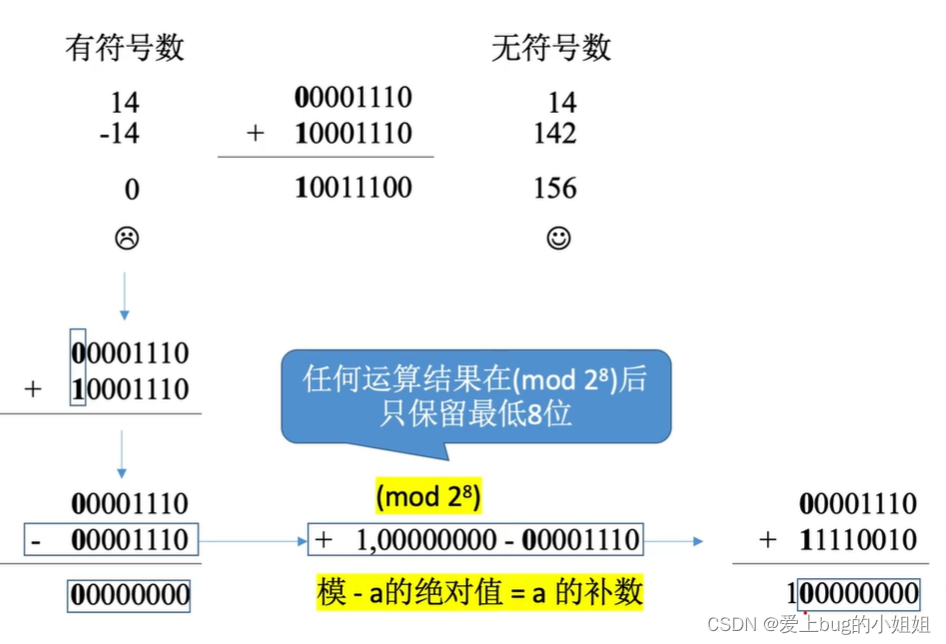
将一个负数的原码转换成补码之后,就可以实现减变加!
ii.移码的作用
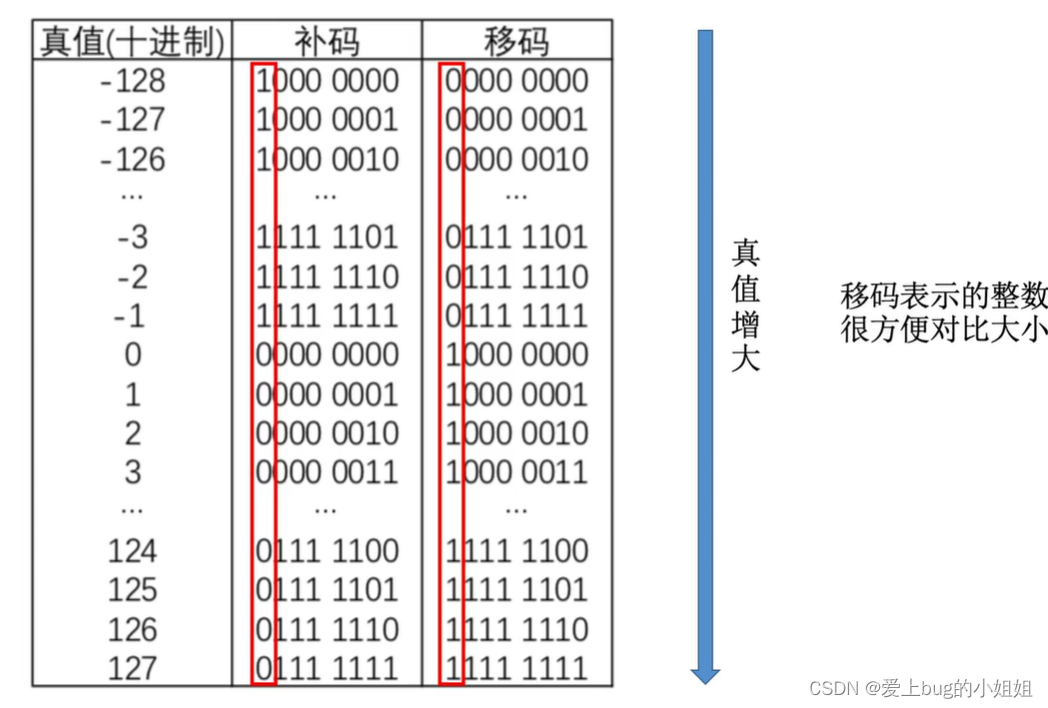
移码只能表示整数,从最高位开始逐位比较,大的该数大。
2、定点数的计算
(1)算数移位
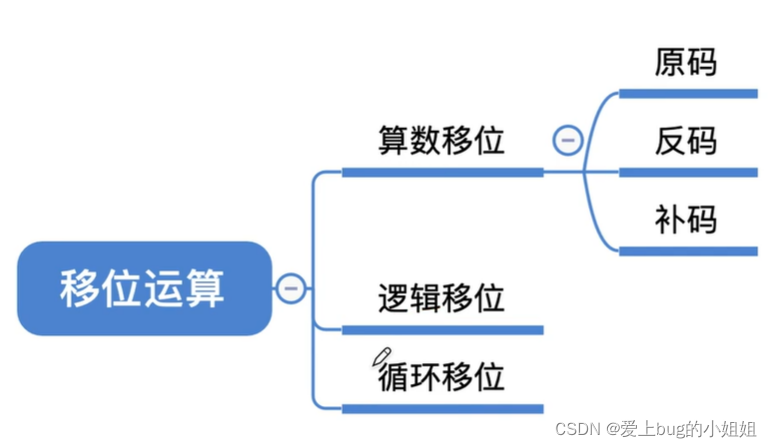
i.算数移位(原码)
移位:通过改变各个数码位和小数点的相对位置,从而改变各数码位的位权,可用移位运算实现乘法、除法。
比如在十进制下:
小数点右移:
- 1001.123小数点右移一位变成了10011.23,相当于乘以10
- 1001.123小数点右移两位变成了100112.3,相当于乘以100(10的平方)
-
1001.123小数点右移三位变成了1001123.0,相当于乘以1000(10的三次方)
小数点左移:
- 1001.123小数点左移一位变成了1001.123,相当于除以10
- 1001.123小数点左移两位变成了10.01123,相当于除以100
- 。。。
在原码中
,因为定点数,小数点的位置不能动,但是山不动水可动,我们可以对数字进行移动。
原码算数右移:
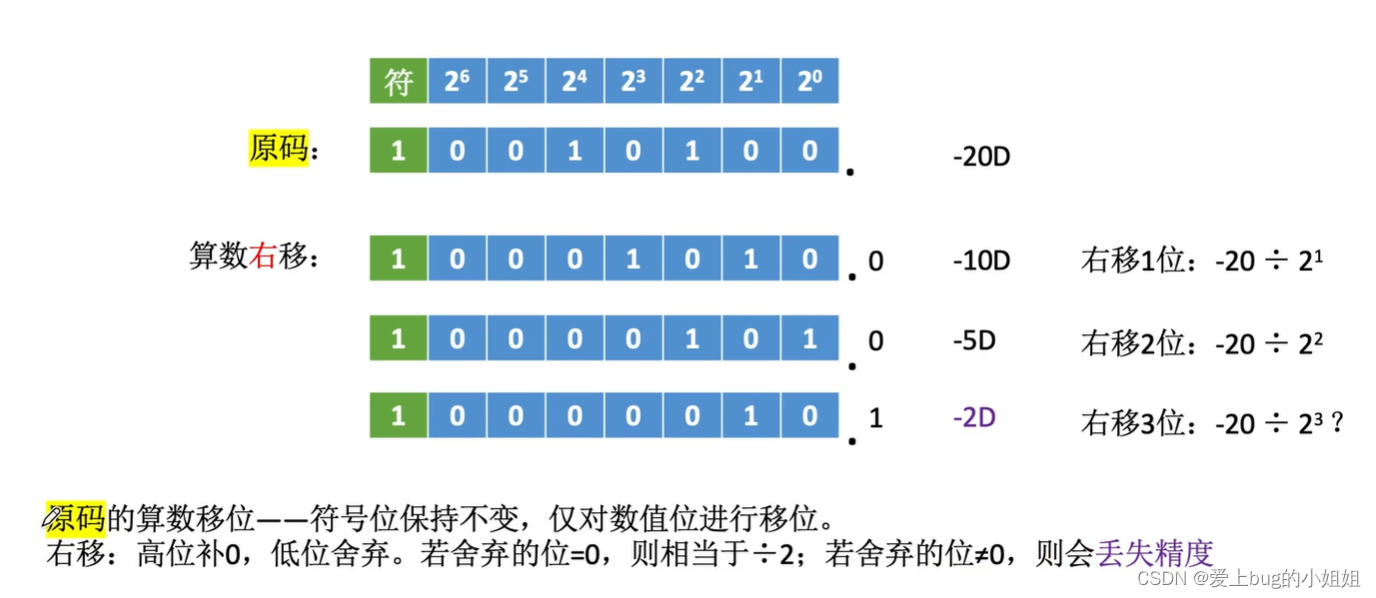
原码算数左移:
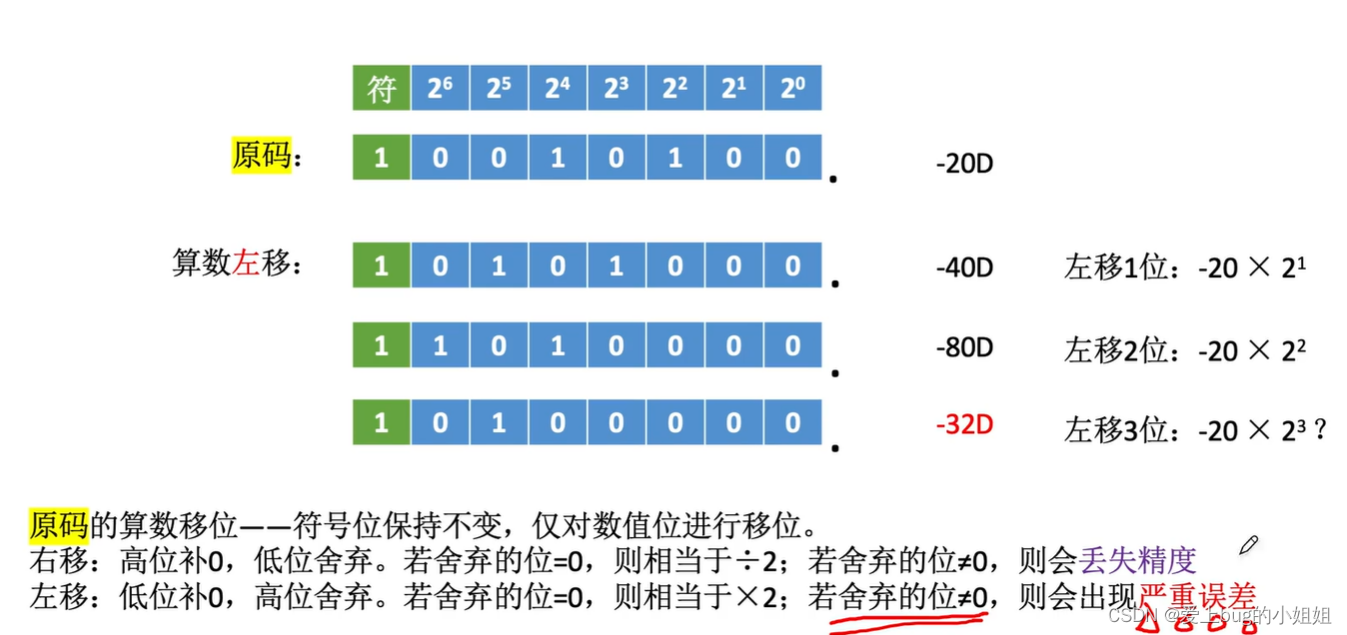
以上的操作都是基于定点整数而言,那对于定点小数又是怎样的呢?
其实是同理的:

ii.算数移位(反码)
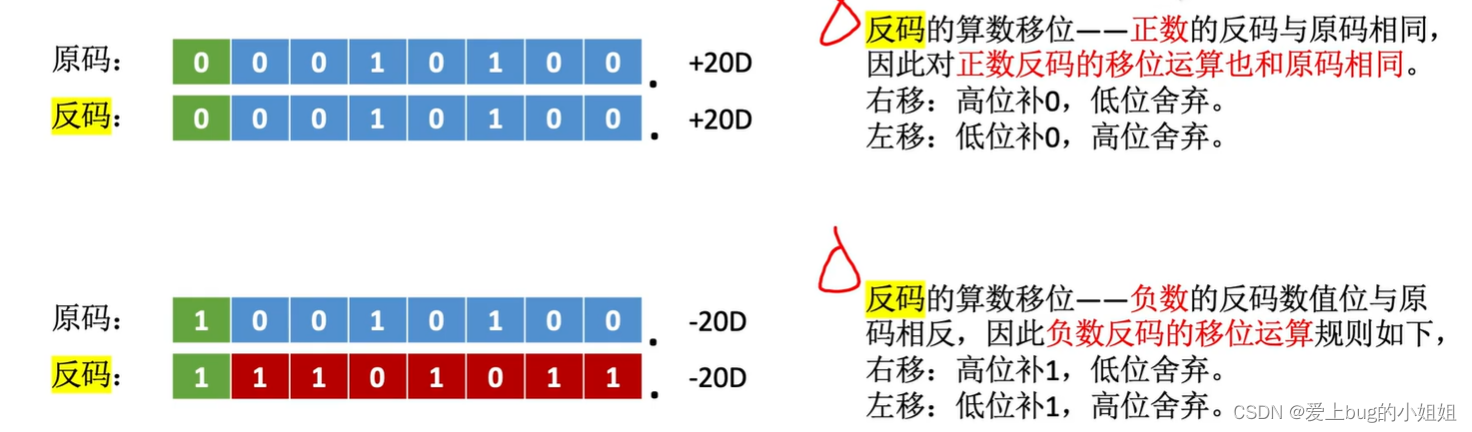
其实也很好理解,正数的原码、反码一样,所以算数移位的方法是一样的,负数的反码是原码取反,而移位的时候原码是补0的,故反码则是0取反为1,补1.
iii.算数移位(补码)
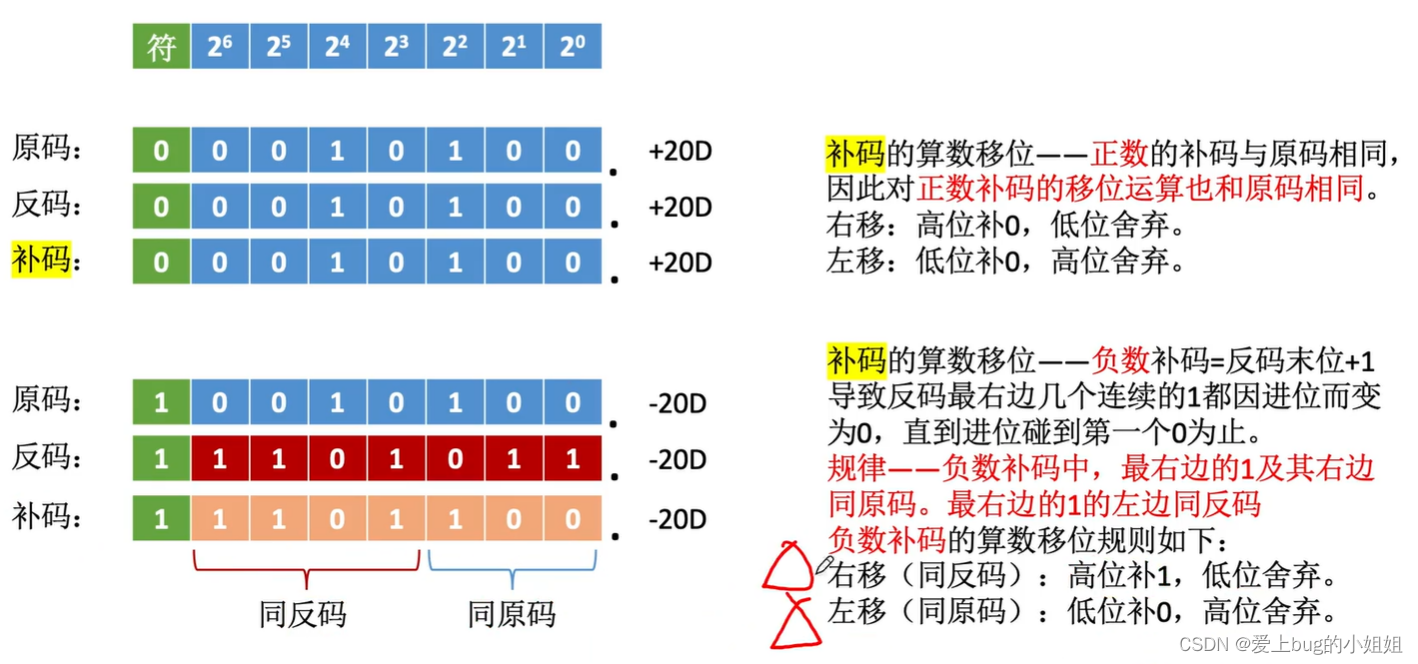
iiii.总结:
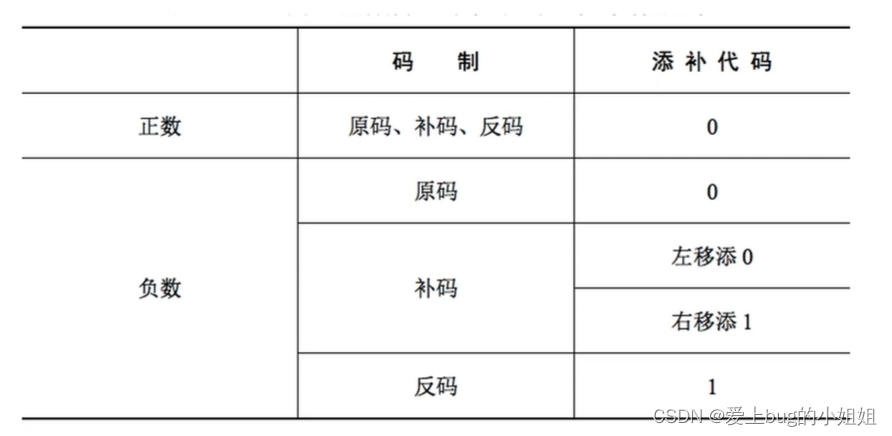
左移相当于乘以2,右移相当于除以2
由于位数有限,因此有时候无法用算数移位精确地等效乘除法。
(2)逻辑移位
逻辑右移:高位补0,低位舍弃。
逻辑左移:低位补0,高位舍弃。
综上,逻辑移位可以看做是对“无符号数”的算数移位。
(3)循环移位
移出的位补充到空缺的位上
4、补码的加减运算
(1)运算

要注意:补码的加减运算和原码、补码之间的转换不同,后者是符号位1不变,其余取反+1,而前者是符号位也参与运算的。
补码转变为原码:
- 符号位不变,其余各位取反+1
- 从右到左,找到第一个非0的位,该位及其右边的位和原码一样,不需要改变,该位的左边和反码一样,直接取反即可
(2)溢出判断

每个字节都有一个表示范围,当超过该范围的上界的时候叫上溢,反之叫下溢。

5、 乘法运算
(1)原码的乘法运算
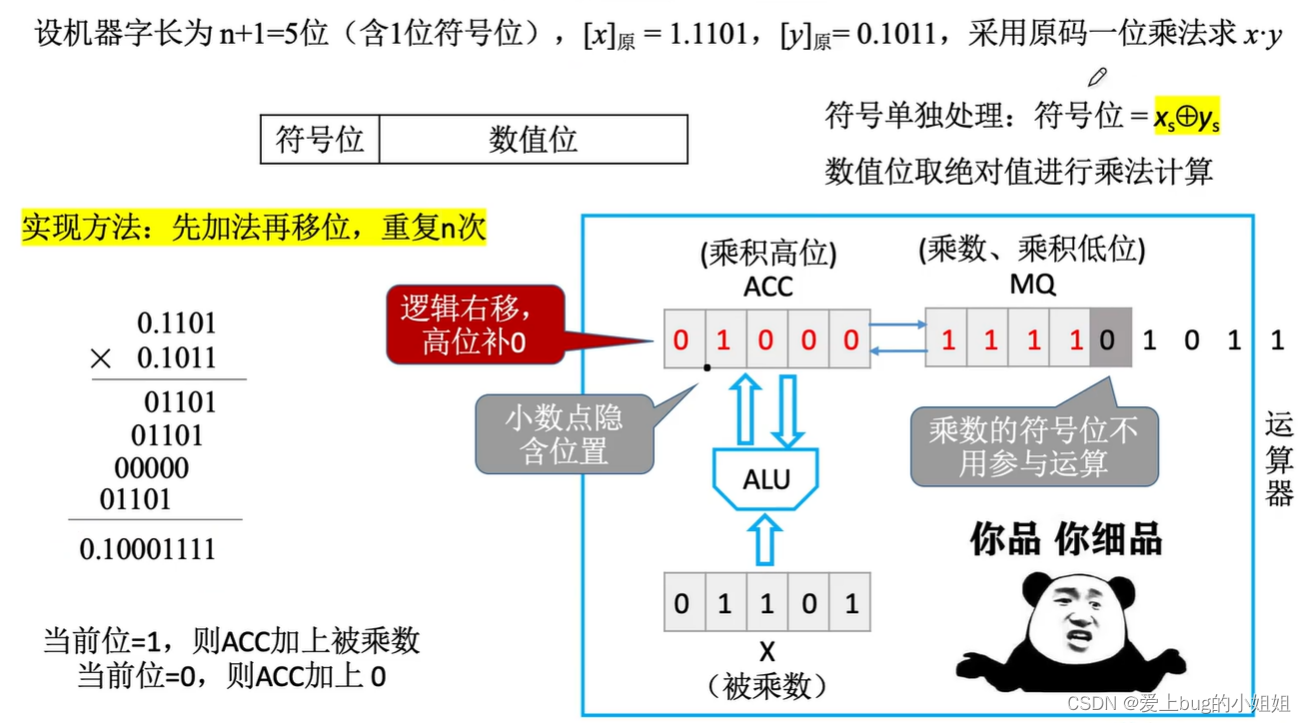
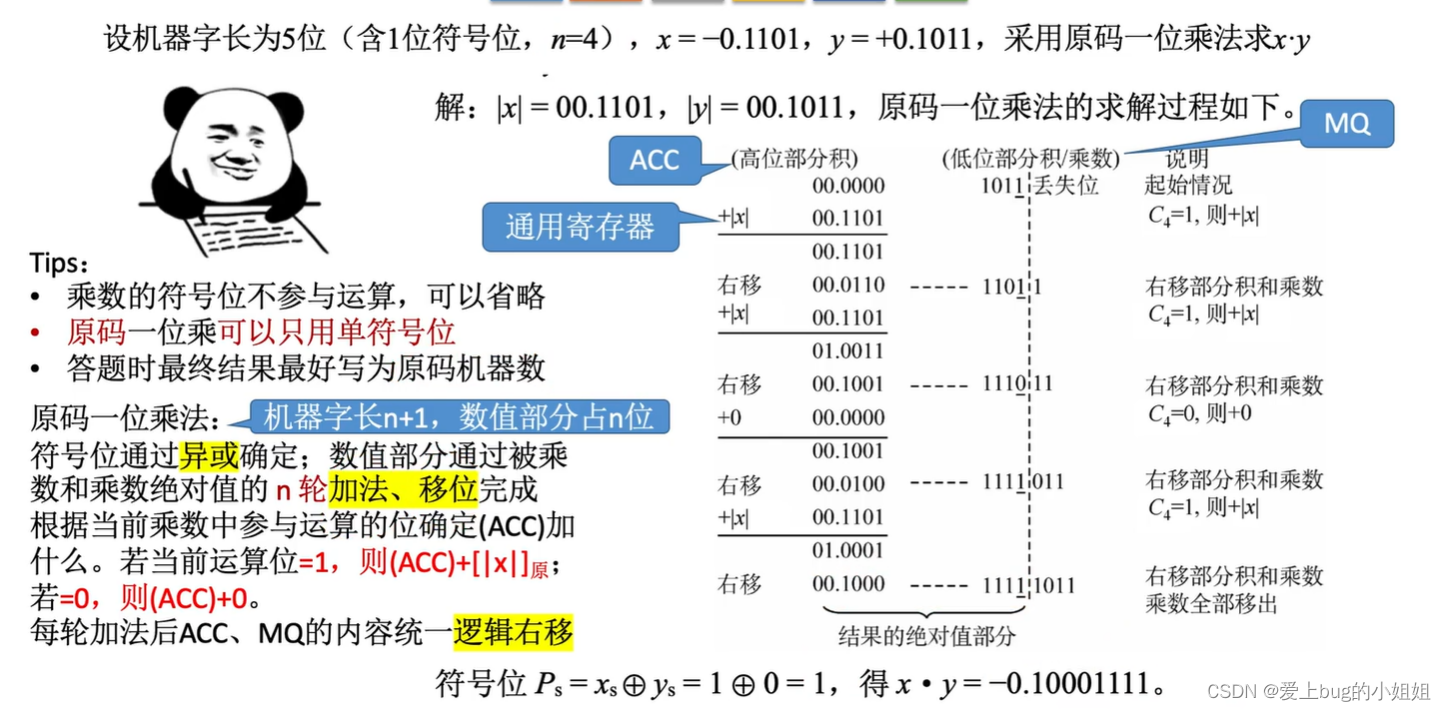
(2)原码的乘法运算
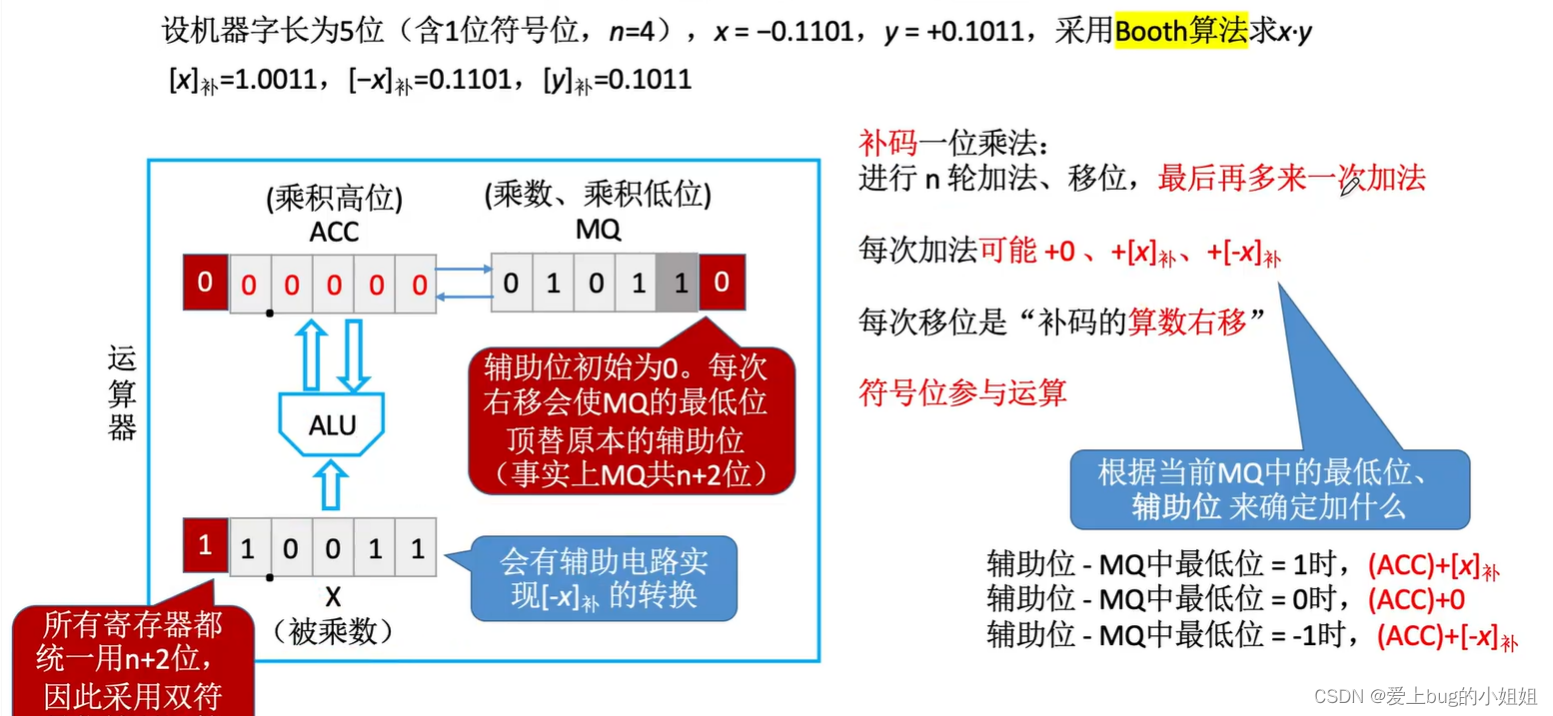

(3)两种乘法的总结

6、除法运算
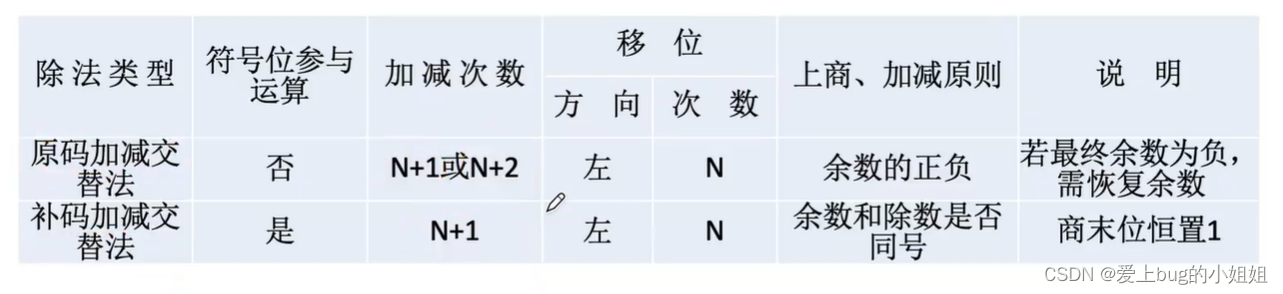
(1)原码的除法
i.恢复余数法
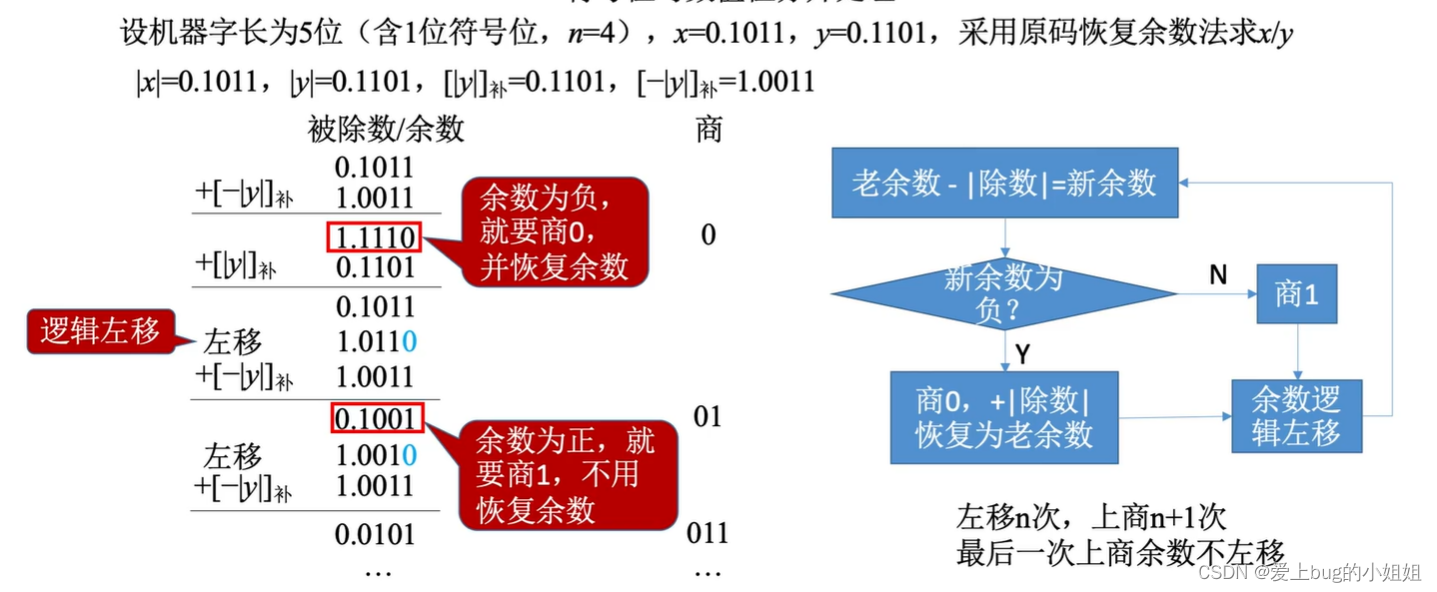
i.加减交替法
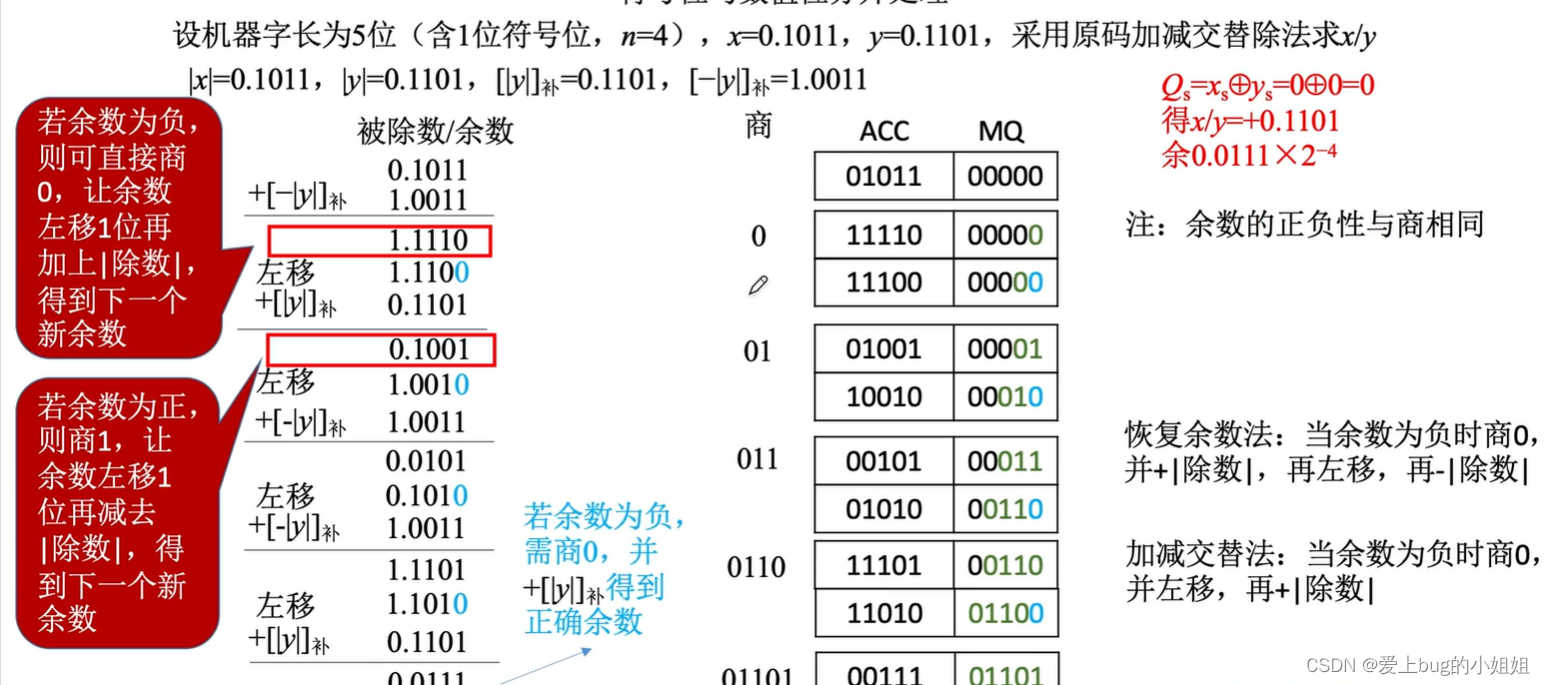
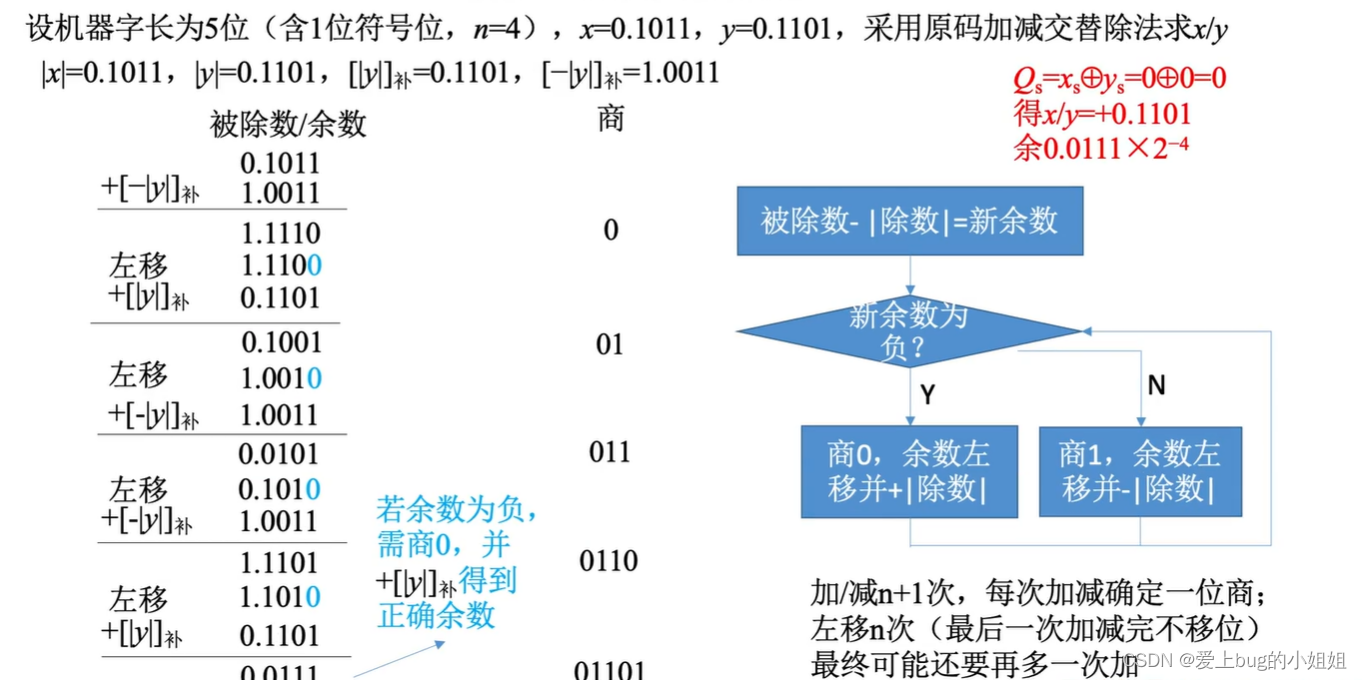
(2)补码的除法(加减交替法)
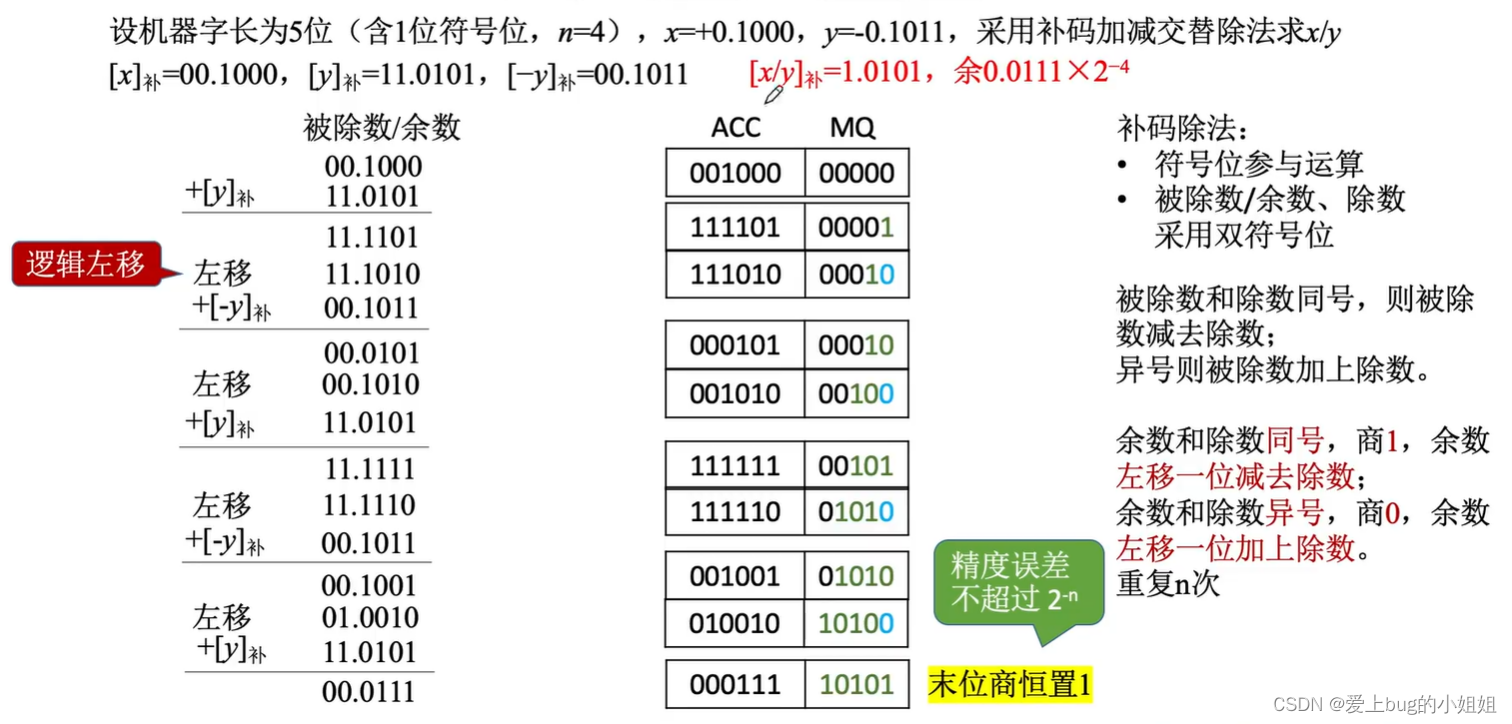
(3)总结:
四、浮点数(对定点数的一个扩展)
1、浮点数的引入
定点小数总有一个范围,范围小,能表示的数据有限,浮点数是对定点数的一个扩展,使得范围扩大(类似科学计数法)



2、浮点数的规格化
浮点数中会存在两种问题,类似是十进制科学计数法中:
- 123.12*10^6
-
0.00123.12*10^11
虽然在手写的情况下发现除了形式不同之外并没有什么大不同,但是在计算机中每一个存储都是有限的(比如8B)在以上两种情况(过多地存储无效位)就有可能会发生溢出,导致精度丢失。
因此,引进了
浮点数尾数的规格化:

对尾数进行规格化,其实就是通过移位(算数移位)将尾数转换成一种特定的形式:
-
原码尾数规格化:
对于正数,则化成0.1xxxx的形式(以0.1开头)
对于负数,则化成1.1xxxx的形式(以1.1开头) -
补码尾数规格化:
对于正数,则化成0.1xxxx的形式
对于负数,则化成1.0xxxx的形式

3、溢出问题
在这里还需要注意一点:
虽然说浮点数是对定点数的扩展,但这并不是说浮点数可以表示所有数据,毕竟有位数限制。
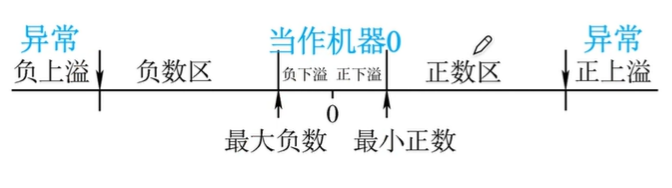
和定点数同理,超出上界的叫上溢,超出下界的叫下溢。
而浮点数还细分为,正上溢、正下溢、负下溢,负上溢
五、全加器
为了避免文章过长,因此以下内容安排在了下一章,敬请各位小伙伴移步指教:
【计算机组成原理】——期末不挂科系列(2)(持续更新ing)