目录
概述
对于一个无向图 G=(V,E) ,它的顶点集 V 可以恰好分为两个不相交的子集,并且在这个无向图中,任意一条边所连接的两个顶点都分别属于这两个不同的子集,那么我们将这个无向图称作
二分图
(如果你愿意也称
二部图
)。
图例:(A中的点没有边直接相连,B同理)

判断二分图
我们可以使用 DFS 的方法对图进行染色,遍历所有点,如果当前点未被染色,则从此点开始进行 DFS 并进行染色,对路径上的点交替染色,如果发现在某个点时矛盾,原图就不为二分图。
时间复杂度为 O(N),空间复杂度为 O(N+E)。
算法实例
接下来,用一个例子说明染色的过程
给定一张图
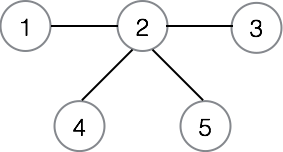
下面我们开始染色,节点 1 未被染色,我们从 1 开始进行 DFS。
先将 1 染成黄色(其他颜色也可以)。
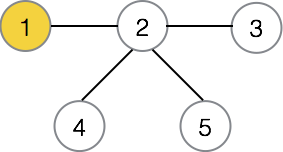
我们发现 2 与 1 直接相连且未被染色,就继续搜索 2,染成蓝色。

我们发现 3 与 2 直接相连且未被染色,就继续搜索 3,染成黄色。

再没有与 3 相连的其他边了,所以我们回溯到 2 ,继续染 4 为黄色,类似 5 也是,最后全染完了就得到了二分图判断和分组结果。

那么,
一个无向图在什么情况下不能成为一个二分图呢?
当无向图中不存在
奇环(结点个数为奇数的环)
时,该图就可以成为二分图,反之就不能成为二分图。
例如这张图:
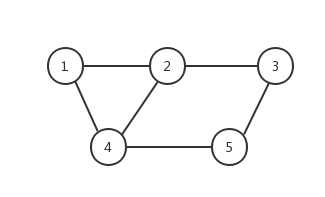
首先,我们把 1 染成黄色:
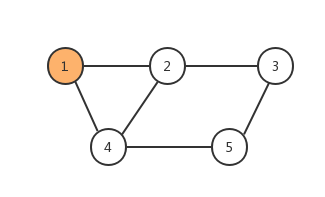
接下来,我们把与 1 相邻的 2,4 染成蓝色:

接下来,我们把与 2 相邻的 3 染成黄色:
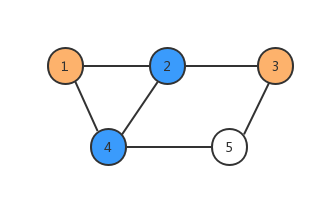
这时我们发现,5 因为和 4 相邻,所以要被染成黄色;同时还和 3 相邻,所以要被染成蓝色。因此,这个图不能称为一个二分图。
C++ 示例代码
为了便于理解,我们令二分图的两组分别染成颜色 1 和颜色 2 ,未染色的点的颜色标记为 0。
//时间复杂度:O(m+n)
//二分图判定:当且仅当一个图中不含奇数环
//此算法可以判定二分图:黑->白->黑->白……
#include<iostream>
#include<cstdio>
#include<cstring>
#define _for(i,a,b) for (int i=(a);i<=(b);i++)
using namespace std;
const int N=1e5+5,M=2e5+10;//N是点的上限,M是边的
int h[N],e[M],ne[M],idx;//单链表
int color[N];//染成i色的点
void init(){
idx=0;
memset(h,-1,sizeof(h));
}
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
bool dfs(int u,int c){
color[u]=c;
for (int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if (!color[j]){
if (!dfs(j,3-c)){
return false;
}
}else if (color[j]==c){
return false;
}
}
return true;
}
int main(){
init();
int n,m;
scanf("%d%d",&n,&m);
while (m--){
int a,b;
scanf("%d%d",&a,&b);
add(a,b),add(b,a);
}
_for(i,1,n){
if (!color[i]){
if (!dfs(i,1)){
puts("No");
return 0;
}
}
}
puts("Yes");
return 0;
}