本文的例子来源于2011年发布的论文 IC3: Where Monolithic and Incremental Meet
Ⅰ、变迁系统的介绍
状态图
论文中给出了一个系统的状态迁移图和它的的变迁公式。现在用三个布尔值的合取来表示某一个状态的值。比如q
0
状态,aka 初始状态,其值分别为 x
1
= false ,x
2
= false ,x
2
= false 。q
0
的简单表示就是 000。论文中又写道,q
3
is ¬x
1
∧ x
2
∧ x
3
,即 011。那么将状态 q 就可以理解为三个二进制位依次加 1 的结果。具体状态迁移图如下所示。
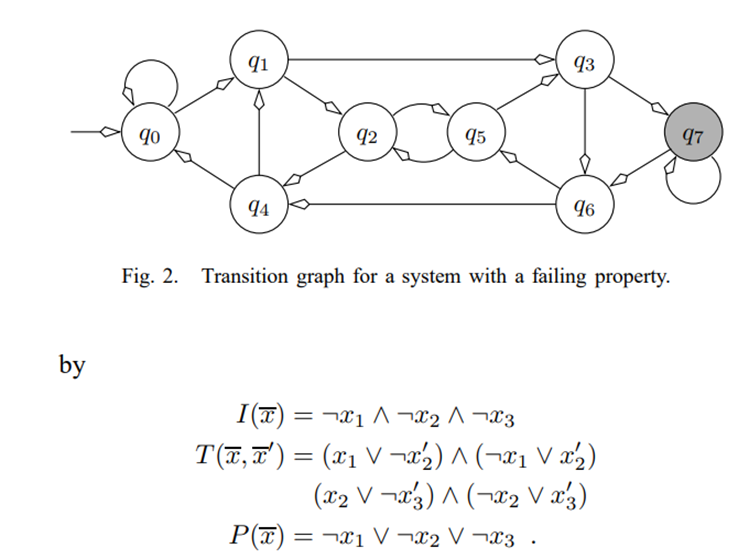
变迁公式
变迁公式由三个组成,其分别为 初始状态,迁移关系 和 安全属性。安全属性在本文的范畴内先不做考虑
因为用不到
。其中的 x ’ 就表示经过变迁后的 x 的下一个状态。以上图的 T 函数(变迁关系)为例,其输入为x 和 x ’ ,上图的 X拔 为三个布尔值的合取,可以参考初始状态 I。而当一个状态集合 S(X) 和 变迁公式 T 进行合取时,如果存在一个状态 即 下图的公式可满足(参考可满足性问题)那么 X拔 的赋值(即X的下一个状态就得到了)。
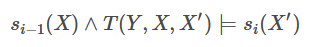
Ⅱ、SMT求解机
简介
其主要用于检查逻辑表达式的可满足性,可以计算实数,也可以计算布尔逻辑公式。目前使用过的分别是SMTinterpol(其支持插值计算)和 Z3(Microsoft公司发明的)。后者的扩展性较好,前者目前好像只支持Java语言。两者的语法规范都是兼容SMT-LIB 2.6的。本次的求解机我也是使用一份代码,两个求解机都进行了运行。
本次使用到的语法规则有,使用(set-option :print-success false)命令来让求解器不输出对每条指令的处理结果
好像在线版会直接省略掉中间步骤
;使用(set-option :produce-interpolants true)开启插值计算。 同时,对于不能自动推断SMT-LIB中公式所使用的理论逻辑的求解器,可以使用(set-logic QF_UFLIA)指定对应的理论逻辑。 使用(assert (! A :named name))形式的命令(SMT-LIB代码),可以添加一个名字(named:)为name的公式A。 注意以上命令中的!符号,不是表示取非,而仅仅是一个形式记号。
公式的计算
有了上述的内容,直接展示如下代码。将下述代码输入到在线版的求解机中即可。
SMTinterpol
和
Z3
,Z3 的在线版不支持额外选项的启用,即set-option。
(set-option :print-success false)
(set-option :produce-proofs true)
(set-option :proof-level lowlevel)
(set-logic QF_LIA)
(declare-fun x1 () Bool) ; 声明布尔变量 x1
(declare-fun x2 () Bool) ; 声明布尔变量 x2
(declare-fun x3 () Bool) ; 声明布尔变量 x3
(declare-fun x11 () Bool) ; 声明布尔变量 x1'
(declare-fun x22 () Bool) ; 声明布尔变量 x2'
(declare-fun x33 () Bool) ; 声明布尔变量 x3'
; 定义 S(x) 函数 aka 当前的状态
(define-fun S ((x Bool)) Bool
(and (not x1) x2 (not x3))
)
; 定义 T(x, x') 函数
(define-fun T ((x Bool) (xx Bool)) Bool
(and (or x1 (not x22)) (or (not x1) x22) (or x2 (not x33)) (or (not x2) x33)
)
)
(assert (and (S (and x1 x2 x3)) (T (and x1 x2 x3) (and x11 x22 x33)) )) ; 断言 S(x) ∧ T(x, x')
(check-sat) ; 检查是否存在满足约束的解
(get-model)
最终得到的运行结果显示 x11 false, x22 false, x33 true。表示从010的状态输入,根据变迁关系T 其下一个状态为001。

计算另一状态
根据状态迁移图我们得知,从一个状态出发,应该有两个后续状态。因此我们对求解的代码进行修改,删除我们已经得到的状态,如果还存在使得SMT求解机返回SAT的情况,就得到了状态迁移的另一个状态。
具体如下代码所示,也就是将上一个代码得到的状态进行合取其的非。表示在排除了这种状态的前提下去寻找满足 S(x) ∧ T(x, x’) 的状态。
(set-option :print-success false)
(set-option :produce-proofs true)
(set-option :proof-level lowlevel)
(set-logic QF_LIA)
(declare-fun x1 () Bool) ; 声明布尔变量 x1
(declare-fun x2 () Bool) ; 声明布尔变量 x2
(declare-fun x3 () Bool) ; 声明布尔变量 x3
(declare-fun x11 () Bool) ; 声明布尔变量 x1'
(declare-fun x22 () Bool) ; 声明布尔变量 x2'
(declare-fun x33 () Bool) ; 声明布尔变量 x3'
; 定义 S(x) 函数
(define-fun S ((x Bool)) Bool
(and (not x1) x2 (not x3))
)
; 定义 T(x, x') 函数
(define-fun T ((x Bool) (xx Bool)) Bool
(and (or x1 (not x22)) (or (not x1) x22) (or x2 (not x33)) (or (not x2) x33)
)
)
;定义 排除状态 函数
(define-fun SS ((x Bool)) Bool
(not(and (not x11) (not x22) x33 ))
)
(assert (and (S (and x1 x2 x3)) (T (and x1 x2 x3) (and x11 x22 x33)) (SS(and x11 x22 x33)) )) ; 断言 S(x) ∧ T(x, x') ∧ S1(x‘)
(check-sat) ; 检查是否存在满足约束的解
(get-model)
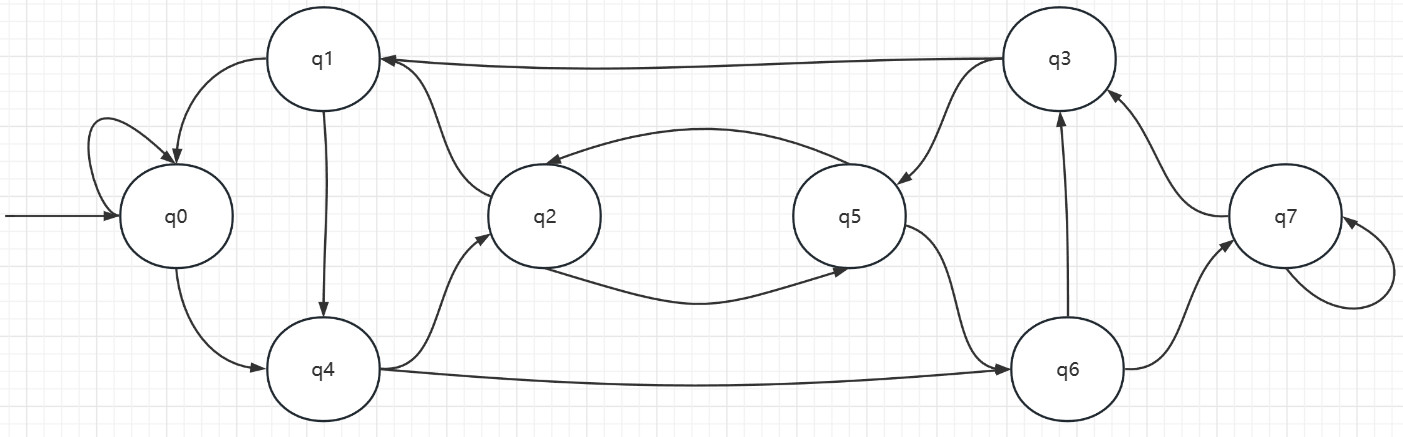
结果展示
根据上述的计算结果,可以绘制出一个新的状态图。最终证明论文中的状态图和状态迁移公式是不匹配的。
| 输入的状态 | 对应x1 x2 x3的值 | 求解返回的第一次结果 | 第二次结果 |
|---|---|---|---|
| q0 | 000 | 000 | 100 |
| q1 | 001 | 000 | 100 |
| q2 | 010 | 001 | 101 |
| q3 | 011 | 001 | 101 |
| q4 | 100 | 010 | 110 |
| q5 | 101 | 010 | 110 |
| q6 | 110 | 011 | 111 |
| q7 | 111 | 011 | 111 |
参考文献