PCA、协方差矩阵以及在点云处理中的应用

文章目录

PCA、协方差矩阵以及在点云处理中的应用

目的

考虑一个问题：一组数据

X_{P\times N}

$X_{P \times N}$

(数据维度为P，样本点数目为N)，我们想对

X

$X$

进行降维，但最大限度的保留其中的信息，该怎么做？

一种直观的想法是这样的，如果数据中存在高度相关的维度，那我们只保留其中的一个维度就可以了。对于普通的数据，各维度的相关性比较复杂，判断要保留哪些维度是一件比较困难的事情。但是有一种理想的情况，数据的协方差矩阵

XX^T

$X X^{T}$

是一个对角矩阵，各个维度之间都不相关，那么我们只需要保留方差比较大的维度就可以了。

所以，如果我们能有一种方法对数据进行处理，使得其协方差矩阵为对角矩阵，即将

(

)

(

)

(

)

(

)

]

\begin{bmatrix} conv(X,X) & conv(X,Y) \\ conv(Y,X) & conv(Y,Y) \end{bmatrix}

$[c o n v (X, X) c o n v (Y, X) c o n v (X, Y) c o n v (Y, Y)]$

化为：

(

)

(

)

]

\begin{bmatrix} conv(X,X) & 0 \\ 0 & conv(Y,Y) \end{bmatrix}

$[c o n v (X, X) 0 0 c o n v (Y, Y)]$

那么问题就解决了。幸运的是，由于协方差矩阵的良好性质（对称性），这个思路是完全可行的。我们可以对原始数据进行”变基“操作（即换个坐标系，或者简单的理解为旋转坐标系），使得这组数据在我们的新基下，其协方差矩阵为对角矩阵。在方差较大的维度上，数据是较为分散的，保留了原始数据的大部分信息。而在方差较小的维度上，数据几乎没有波动，这些维度我们完全可以丢掉。因此可以起到降维的效果。（当我们的新基相对与旧基只是一个旋转变换的时候，各样本点到样本均值之间的距离是不变的。这个距离的均值等于协方差矩阵的迹，也即各个维度内部的方差之和。因此一些维度方差最大，另一些维度必然方差最小）。

以上就是PCA算法的基本思想。

PCA推导

特征值分解

定义：

方阵

A_{n\times n}

$A_{n \times n}$

,且

A

$A$

有

N

$N$

个线性无关的特征向量

(

…

)

q_{i}(i=1, \ldots, N)

$q_{i} (i = 1, \dots, N)$

，则

A

$A$

可以被分解为

−

\mathbf{A}=\mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{-1}

$A = Q Λ Q^{- 1}$

其中

\mathrm{Q}

$Q$

是

N \times N

$N \times N$

方阵, 且其第

i

$i$

列为

\mathrm{A}

$A$

的特征向量。

\Lambda

$Λ$

是对角矩阵, 其对角线上的元素为对应的特征值，也即

\Lambda_{i i}=\lambda_{i}

$Λ_{i i} = λ_{i}$

。

直观理解：

矩阵乘法可以表征一个线性变换（旋转和拉伸的组合，注意方阵没有降维操作），特征值分解可以使得这个过程更加清晰。首先需要说明的是，

A

$A$

代表的线性变换，在以其特征向量为基的空间中，只是沿着坐标轴的拉伸而已（两者是同一个线性变换在不同的坐标系下的表达，也即

A

$A$

与

\mathbf{\Lambda}

$Λ$

是相似矩阵）。所以假设我们要对向量

b

$b$

进行线性变换（求

Ab

$A b$

），可以分解为以下三步：

对
$q_i q i 为基底的坐标系下，得到 b q b_q b q （左乘 Q − 1 Q^{-1} Q − 1 ）$
对
$b_q b q 沿着坐标轴拉伸 (左乘 Λ \Lambda Λ )$
将
$b_q b q 进行”反变基”，变回原坐标系下（左乘 Q Q Q )$

一些细节：

记录下实对称矩阵的优良性质：
- 实对称矩阵的特征值都是实数。这时矩阵的几何意义可以认为是沿着特征向量的拉伸和缩放
- 实对称矩阵不同的特征值对应的特征向量是正交的，普通矩阵只能保证不同的特征值对应的特征向量线性无关（要求正交的话，可以使用正交化方法）
- 实对称矩阵的
- 实对称矩阵必可正交相似对角化，即必存在正交矩阵
  $\mathbf{Q} Q ,使得 Q − 1 A Q \mathbf{Q}^{-1} \mathbf{A} \mathbf{Q} Q − 1 A Q 为对角矩阵, 其中 Q \mathbf{Q} Q 的列向量为 A \mathbf{A} A 的正交特征向量。（首先因为n阶实对称矩阵有n个线性无关的特征向量，因此是必可对角化的;其次，其 k k k 重特征值所对应的特征向量虽然只能保证线性无关，但是我们可以对其进行施密特正交化（施密特正交化求出来的向量都是这 k k k 个线性无关特征向量的线性组合,因此仍然是原矩阵的特征向量））$
非对称矩阵和复矩阵的特征值可能为复数。这时矩阵的几何意义是旋转，路径不一定是圆，也可以是螺线。特征值可以理解为一个和旋转角度有关的量。

了解了以上内容，我们一开始提出的问题的解决方案就很清楚了。协方差矩阵是一个实对称矩阵，而实对称矩阵必可正交相似对角化，也就是说我们一定可以找到一组新的正交基，把实对称矩阵化为对角矩阵。

对协方差矩阵进行正交相似对角化：

−

\Lambda=P^{-1}X X^{T} P=P^{T}X X^{T} P

$Λ = P^{- 1} X X^{T} P = P^{T} X X^{T} P$

我们所寻找的基变换就是

Y=P^TX

$Y = P^{T} X$

,

P

$P$

的列向量为

XX^T

$X X^{T}$

的正交特征向量。

以上过程，需要求出协方差矩阵，再做特征值分解，当数据量大、数据维度高的时候，这种方法的计算代价很高，我们可以利用奇异值分解做优化。

（PCA另有两种推导思路，最小投影距离及最大投影方差，这里不再赘述，可参考

PCA推导

）

奇异值分解

定义：

对于任意给定的

∈

A\in R^{m\times n}

$A \in R^{m \times n}$

,都存在唯一的正交矩阵

∈

U\in R^{m\times m}

$U \in R^{m \times m}$

,

∈

V\in R^{n\times n}

$V \in R^{n \times n}$

和

∈

S\in R^{m\times n}

$S \in R^{m \times n}$

使得

A=USV^T

$A = U S V^{T}$

其中:

U

$U$

的列向量为

AA^T

$A A^{T}$

的特征向量，称为

A

$A$

的左奇异向量

V

$V$

的列向量为

A^TA

$A^{T} A$

的特征向量，称为

A

$A$

的右奇异向量

[

]

S=\begin{bmatrix} S_1 & 0 \\ 0 & 0 \end{bmatrix}\\

$S = [S_{1} 0 00]$

(

)

(

)

⩾

为

矩

阵

奇

异

值

S_1=diag(\sigma_1,…\sigma_r),r=r(A),\sigma_1\geqslant…\geqslant\sigma_r>0,\sigma_i为矩阵奇异值

$S_{1} = d i a g (σ_{1}, . . . σ_{r}), r = r (A), σ_{1} ⩾ . . . ⩾ σ_{r} > 0, σ_{i} 为矩阵奇异值$

直观理解：

和特征值分解类似，奇异值分解是为了让我们将矩阵所表征的线性变换看得更清晰。为了达到这个目的，我们需要找到新基，使得在这些基下，矩阵所表征的线性变换是一个非常简单的形式。在特征值分解中，我们找到的新基就是特征向量。对于非方阵和无法进行特征值分解的方阵，我们找到的新基是”奇异向量“。奇异向量满足两个性质：

变换前是正交的，变换后仍然正交
在以奇异向量为基的空间中，

举例而言，对于矩阵：

[

]

A=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}\\

$A = [1011]$

这是一个剪切变换，只有一个特征向量

，

)

(1，0)^T

$(1 ， 0)^{T}$

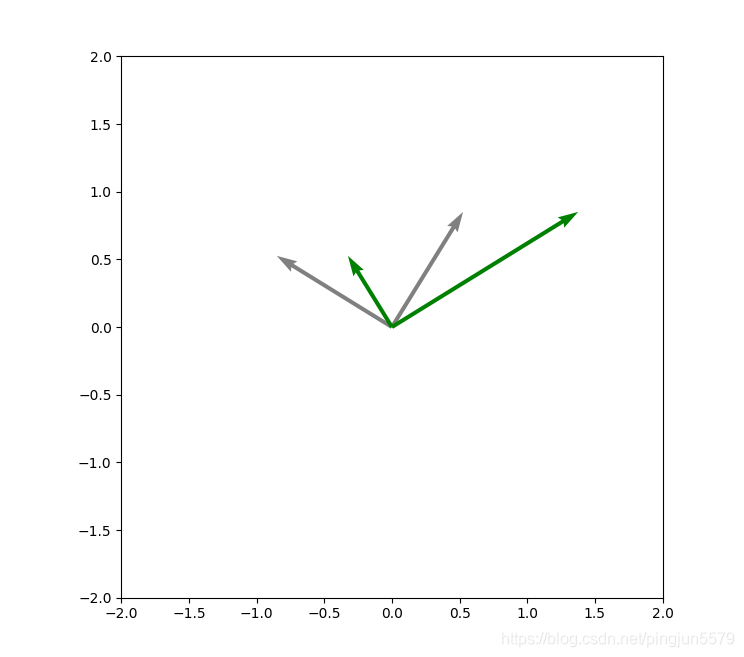
，无法进行特征值分解。如下图所示。

在这里插入图片描述

但是却可以进行奇异值分解（灰色是右奇异向量，绿色是右奇异向量左乘

A

$A$

之后的向量，即经过剪切变换后的向量，可以看到两个向量仍然是正交的;绿色向量较灰色向量的伸缩比例就是奇异值;经过单位化后，就是左奇异向量）：

在这里插入图片描述

奇异值分解，实际上是将一个线性变换

Ab

$A b$

分为了以下三个步骤：

对
$v_i v i 为基底的坐标系下，得到 b v b_v b v （左乘 V T V^T V T ，可以理解为坐标轴的旋转）$
对
$b_v b v 沿着坐标轴拉伸 (左乘 S S S )$
将
$b_v b v 再次进行”变基”，变到以 U U U 的行向量为基的坐标系下（左乘 U U U ，坐标轴再次旋转)$

图示如下：

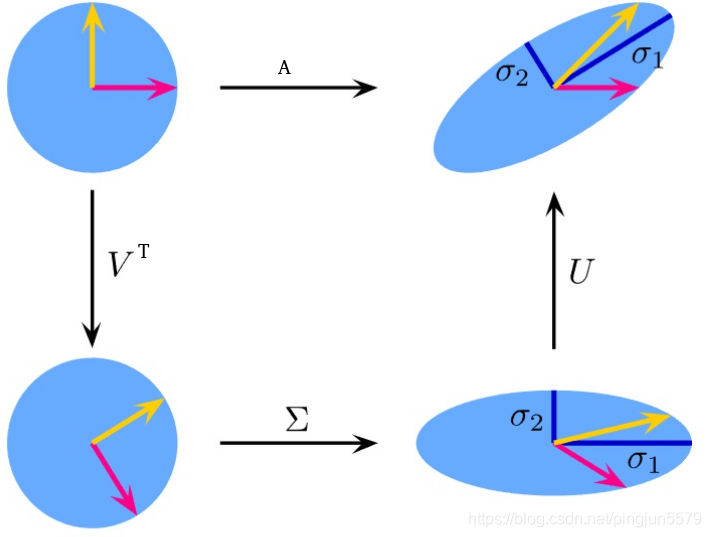
在这里插入图片描述

（线性变换

A

$A$

将单位圆变成了椭圆，

A

$A$

的奇异值即是该椭圆的长轴与短轴）

奇异值分解同特征值分解的关系

$AA^T A A T 的特征值等于 A A A 的对应奇异值的平方$
$AA^T A A T 的特征向量， V V V 的列向量为 A T A A^TA A T A 的特征向量$

在上节内容中，为了对角化数据

X

$X$

协方差矩阵，我们所寻找的基变换是

Y=P^TX

$Y = P^{T} X$

,

P

$P$

的列向量为

XX^T

$X X^{T}$

的正交特征向量。有了奇异值分解，我们无需再对解协方差矩阵做特征值分解，而只需要对

X

$X$

做奇异值分解就可以了，因为左奇异向量就是

XX^T

$X X^{T}$

的正交特征向量。

协方差矩阵的几何意义

有了以上的讨论，我们再回过头来看看协方差矩阵的几何意义，就比较简单了，总结一下：

协方差矩阵的最大特征值对应的特征向量，总是指向方差最大的方向；次最大特征值对应的特征向量，正交于最大特征值对应的特征向量，并指向次最大方差指向的方向
协方差矩阵可以让我们了解附加在原始数据上的线性变换的信息。

假设我们有一组原始数据

X

$X$

，协方差矩阵为单位阵

I

$I$

(比如一个协方差矩阵为

I

$I$

二元正态分布)。我们对

X

$X$

做了一个线性变换( 限定这个线性变换只包含旋转和拉伸，即

=

R

S

A=RS

$A = R S$

,

R

$R$

为旋转矩阵，

S

$S$

为拉伸矩阵），得到

X

AX

$A X$

，那么

X

AX

$A X$

的协方差矩阵为

X

X

T

A

T

=

A

A

T

=

R

S

S

R

T

AXX^TA^T=AA^T=RSSR^T

$A X X^{T} A^{T} = A A^{T} = R S S R^{T}$

,又从特征值分解的角度

A

T

=

Q

Λ

Q

−

1

AA^T=\mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{-1}

$A A^{T} = Q Λ Q^{- 1}$

,所以

=

Q

,

S

S

=

Λ

R=Q,SS=\mathbf{\Lambda}

$R = Q, S S = Λ$

.也就是说，

A

T

AA^T

$A A^{T}$

的特征向量说明了原始数据是如何被旋转的，特征值则说明了原始数据是如何被拉伸的。

点云处理中的应用

PCA方法在点云处理中有很多应用，列以下几种：

边缘检测：位于边缘处的点云有什么特点？从线性变换的角度看，就是存在一个维度，点云拉伸的程度很大，另外两个维度则比较小。因此点云协方差矩阵的特征值可以反映一个点是否是边缘点。我们可以计算
$\lambda_{1}/(\lambda_{1}+\lambda_{2}+\lambda_{3}) λ 1 / ( λ 1 + λ 2 + λ 3 ) ,( λ 1 , λ 2 , λ 3 \lambda_{1},\lambda_{2},\lambda_{3} λ 1 , λ 2 , λ 3 按照从大到小的顺序排列)，超过阈值则认为是边缘点$
法向量计算：再想象一组呈平面分布的点云，我们想求其法向量，那实际上是找到新的基向量
$e_1，e_2，e_3 e 1 ， e 2 ， e 3 ,使得点云在 e 1 ， e 2 e_1，e_2 e 1 ， e 2 方向上最为分散，而在 e 3 e_3 e 3 上最为集中。 e 3 e_3 e 3 即是我们要求的法向量。见法向量计算$
点云的Oriented Bounding Box（方向包围盒）的计算，可以使用PCA计算出OBB的主轴。见

OBB计算
点云的粗配准，可以使用PCA得到位姿的初始估计。

参考链接

https://blog.csdn.net/P081513083/article/details/104389658

https://www.zhihu.com/question/41120789/answer/481966094

https://blog.csdn.net/linmingan/article/details/80586214

协方差矩阵的直观解释

https://www.zhihu.com/question/22237507

https://www.cnblogs.com/bjwu/p/9280492.html

原文链接：https://blog.csdn.net/pingjun5579/article/details/118882657