整数拆分的含义:将整数n拆分成k个数的和。
整数拆分分为有序拆分和无序拆分两种。
先看
无序拆分
:顾名思义,拆分不考虑顺序,如将4拆分成3+1和1+3算一种方案。
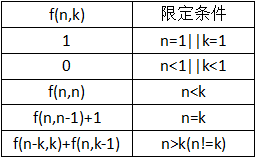
无序拆分的精髓在于其递推公式。假设整数n被拆分为最大数不超过k的方案数为f(n,k) (n>=k,k>=1),(注:整数n被无序拆分为最多k个数的方案数即为整数n被拆分为最大数不超过k的方案数,根据Ferrers图像的某个推论)
1)n=1,即拆分整数1,只有一种拆分方案,所以f(1,1)=1;
2) k=1,即将整数n拆分为一个数,那就是整数本身喽,所以f(n,1)=1;
3) n>k(n!=k),f(n,k)=f(n-k,k)
[包含k的那些拆分方案]
+f(n,k-1)
[不包含k的那些拆分方案]
(
这里重点理解
);
4)n=k;f(n,k)=f(n,n)=f(n,n-1)
[不包含n的那些拆分方案]
+1[
包含n的拆分方案,也就是把n拆分成n,所以方案数为1
] (
这里重点理解
);
5)n<1,f(n,k)=0,n<1,没有办法拆分,所以没有方案,方案数就是0喽;
6)k<1,f(n,k)=0,理由同5);
7)n<k,f(n,k)=f(n,n),因为k都大于n了,n根本没有办法划分出k,n能划分出的最大数是n;
综上,
贴一段java代码吧
public static int count(int sum, int max) {
if (sum < 1 || max < 1) return 0;
else if (sum == 1 || max == 1){
return 1;
} else if (sum < max) {
return count(sum,sum);
} else if (sum == max) {
return 1+count(sum, sum-1);
} else {
return count(sum, max-1)+count(sum-max,max);
}
}
好了,代码就是按照上面的7个限定条件写的,很容易理解了。
接下来研究
有序拆分
,将整数n拆分为k个数(
这里注意与有序拆分对比,有序拆分那里是最多k个数
)可以这样理解:将n个完全相同的小球分为k堆(每堆的小球数都大于等于1),使用插空大法,可以得出方案数为c(n-1,k-1).
将整数n拆分为
最多n个数(1个数,2个数…n个数)
的方案数为c(n-1,0)+c(n-1,1)+…+c(n-1,n-1) =pow(2,n-1) .
有序拆分这里举一个
招行笔试题
, 题的大意是这样的,将n块巧克力分给最多n个小朋友,给第一个小朋友至少分6块,剩余的小朋友如果能分到巧克力的话,至少分一块,也就是可能说有的小朋友是分不到巧克力的,题目要求是编程求解可能的巧克力分发方案数。
分析一下,因为小朋友是有区别的,所以很明显看出这个题目其实是整数的有序拆分。但是有限定条件,就是第一个小朋友
至少
(
这里要好好理解至少的含义,至少就是大于等于嘛
)分6块巧克力,分情况讨论:
1)第一个小朋友分到6块巧克力
那就先取出六块巧克力分给第一个小朋友,此时题目变成将n-6块巧克力分给最多n-6个小朋友(注意这里的n-6个小朋友不包括第一个小朋友),由上面整数有序拆分公式,方案数为pow(2,n-7);
2)第一个小朋友分到大于6块巧克力
同样先取出6块巧克力分给第一个小朋友,此时题目变成将n-6块巧克力分给最多n-6个小朋友(注意这里的n-6个小朋友包括第一个小朋友),方案数为pow(2,n-7);
综上,分巧克力的方案数为2*pow(2,n-7)=pow(2,n-6);这个就是最后的答案,直接编程输入n,然后计算pow(2,n-6),程序就可以被AC。看来有的编程注重考查思想啊。。。。。