1、变量符号含义

1、训练集
D
=
{
(
x
⃗
1
,
y
⃗
1
)
,
(
x
⃗
2
,
y
⃗
2
)
,
.
.
.
,
(
x
⃗
m
,
y
⃗
m
)
}
D = \{(\vec{x}_1, \vec{y}_1), (\vec{x}_2, \vec{y}_2),…, (\vec{x}_m, \vec{y}_m)\}
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
m
,
y
m
)
}
,共m个样例
2、
x
⃗
i
∈
R
d
,
y
⃗
i
∈
R
d
\vec{x}_i \in \mathbb{R}^d, \vec{y}_i \in \mathbb{R}^d
x
i
∈
R
d
,
y
i
∈
R
d
:输入样本由
d
d
d
个属性描述,输出
l
l
l
维(
l
l
l
个属性描述)实值向量
y
⃗
i
\vec{y}_i
y
i
3、对应图中的神经网络
- d个输入神经元:输入特征向量由d个属性描述
- l个输出神经元:输出特征向量由y个属性描述
- q个隐层神经元:拟合数据集线性不可分时的模型
4、连接权都如图所示
5、激活函数:sigmoid

6、阈值:每个神经元都有自己的阈值
-
输出层第
jj
j
个神经元
yi
y_i
y
i
的阈值:
θi
\theta_i
θ
i
-
隐层第
hh
h
个神经元
bh
b_h
b
h
的阈值:
γh
\gamma_h
γ
h
7、第x个神经元的输入:FNN都是全连接,因此要求和
-
输出层第j个神经元的输入:
βj
\beta_j
β
j
-
隐层第h个神经元的输入:
αh
\alpha_h
α
h
2、损失函数:均方误差推导
1、训练样例
(
x
⃗
k
,
y
⃗
k
)
(\vec{x}_k, \vec{y}_k)
(
x
k
,
y
k
)
2、其经过神经网络的
l
l
l
个输出记为
y
⃗
^
k
=
(
y
1
^
k
,
y
2
^
k
,
.
.
.
,
y
l
^
k
)
\hat{\vec{y}}_k = (\hat{y_1}^k,\hat{y_2}^k, …,\hat{y_l}^k )
y
^
k
=
(
y
1
^
k
,
y
2
^
k
,
.
.
.
,
y
l
^
k
)
,其中每个输出:

3、则对于这一个训练样例
(
x
⃗
k
,
y
⃗
k
)
(\vec{x}_k, \vec{y}_k)
(
x
k
,
y
k
)
,网络的均方误差为:
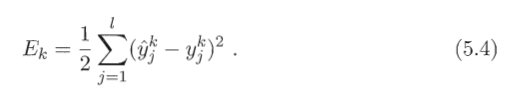
3、算法:求参数w和θ,BP算法,基于
随机
梯度下降
3.1 随机梯度下降的理解
梯度是有方向的:曲面上方向导数的最大值的方向就代表了梯度的方向
因此每次规定的步长
η
\eta
η
固定,我们的
参数
就要朝着该参数对应函数梯度的方向(变化最快,如山最陡峭的方向)变化,才能让
损失函数值
最快地往极小值收敛。
理解:假设你初始在山顶,步长5m,朝着梯度最大(最陡峭的)方向,走5m(也就是当前点的梯度值*步长),能垂直距离下降4m,非最陡峭方向一次则垂直距离下降更少。
批量梯度下降:
-
对于权值
θ⃗
\vec{\theta}
θ
中的每个分量
θj
\theta_j
θ
j
(个数对应样本属性个数),每次
所有m个样本
的第j个属性值
都要参与更新
Δ值
\Delta值
Δ
值
。 - 更新完所有分量,算作一次批量梯度下降结束。一般我们会重复梯度下降多次

如图代码就是使用批量梯度下降,重复了iters次数,每一次所有样本参与对权值
θ
⃗
\vec{\theta}
θ
中的每个分量
θ
j
\theta_j
θ
j
进行更新。那个np.sum

随机梯度下降:
用样本中的一个随机选取的样本
x
⃗
i
\vec{x}_i
x
i
来近似我所有的样本,来调整θ
-
对于权值
θ⃗
\vec{\theta}
θ
中的每个分量
θj
\theta_j
θ
j
(个数对应样本属性个数),每次
只有样本
x⃗
i
\vec{x}_i
x
i
的第j个属性值
参与更新
Δ值
\Delta值
Δ
值
。 - 更新完所有属性分量,算作一次随机梯度下降结束。一般我们会重复梯度下降多次

3.2 公式推导
求偏导什么时候结果要求和:看连线

-
单独一条隐含层到输出层的连接权w只影响一个y,因此对其求偏导,无需求和。
-
但是输入层到隐含层的连接权v,即使是一条,也会影响所有的y。
-
看图中的连线即可知道。则其实从隐含层的神经元b开始,之后所有的参数,一个都会影响所有的y。故链式法则求偏导时要加上求和符号。

3.3 BP算法

