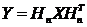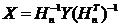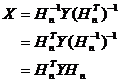博客

代码版本： HM16.2

IDCT（逆DCT）变换是DCT变换的逆变换。在HEVC的解码端对图像的像素残差进行IDCT变换，再进行反量化，就可以得到最初的残差值， 原像素 = 预测值 + 残差值。这篇文章基于HM16.2版本的解码代码进行原理分析以及代码实现。

原理分析：

令： H为编码端的变换矩阵，X为像素值矩阵， Y为变换后得到的像素值矩阵。

变换公式大体为：

。

n为变换矩阵的尺寸，在HEVC中存在4种大小的变换矩阵：4×4, 8×8, 16×16, 32 x32。

在解码端的IDCT公式为：

。

从上式可以看出，解码端相对编码端的求解顺序是类似的，唯一额外的计算为求得变换矩阵的逆矩阵。

通过分析得知在HEVC的DCT变换矩阵为正交矩阵，正交矩阵的特性之一正交矩阵的逆矩阵等于它的转置矩阵。由此可以得到以下推倒公式：



由上式可见，在整个计算过程我们只需要知道变换矩阵H和像素值矩阵Y就可以求得矩阵X。

解码代码分析：（以4x4IDCT为例）

代码实现分两部分组成，第一步为前两个矩阵相乘，保存结果为中间变量；

第二步为中间变量与后一个矩阵相乘。