实验目的
通过实验掌握Matlab直线拟合,多项式拟合,非线性拟合的操作方法,进一步理解最小二乘拟合
理论。
实验内容与步骤
1. 已知一组数据x=[1 1.5 3 4 5 6 6.5 7 8];y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
(1)画出数据的散点图;
(2)分别计算1,4,7次多项式拟合,画出拟合效果图;
1次多项式拟合:
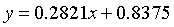
4次多项式拟合:
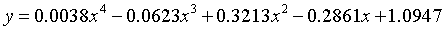
7次多项式拟合:
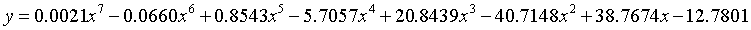
(3)参考幂函数的拟合方法,利用指数函数拟合这组数据,并且画出拟合效果图;由
y
=
a
e
b
x
y = a{e^{bx}}
y
=
a
e
b
x
两边同时取对数可知
ln
y
=
ln
a
+
b
x
\ln y = \ln a + bx
ln
y
=
ln
a
+
b
x
,由此可知只需要一次拟合
ln
y
\ln y
ln
y
与
x
x
x
即可
拟合可得
ln
y
=
0.1483
x
+
0.0081
\ln y = 0.1483x + 0.0081
ln
y
=
0
.
1
4
8
3
x
+
0
.
0
0
8
1
(4)利用残差平方和
∑
i
=
1
n
(
y
i
−
y
‾
i
)
2
\sum\limits_{
{\rm{i}} = 1}^n {
{
{({y_i} – {
{\overline y }_i})}^2}}
i
=
1
∑
n
(
y
i
−
y
i
)
2
(节点处已知的函数值与拟合函数的取值的差的平方和),评价以上拟合效果哪个最好。
一次多项式拟合残差平方和为0.5380
四次多项式拟合残差平方和为0.4634
七次多项式拟合残差平方和为0.0333
幂函数拟合残差平方和为0.6627
由于
0.6627
>
0.5380
>
0.4634
>
0.0333
0.6627 > 0.5380 > 0.4634 > 0.0333
0
.
6
6
2
7
>
0
.
5
3
8
0
>
0
.
4
6
3
4
>
0
.
0
3
3
3
,所以拟合效果:七次多项式>四次多项式>一次多项式>幂函数,七次多项式拟合效果最好
画出数据的散点图:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
plot(x,y,'.')
一次多项式拟合:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
plot(x,y,'.')
p=polyfit(x,y,1)
y1=polyval(p,x);
hold on
plot(x,y1)
四次多项式拟合:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
plot(x,y,'.')
p=polyfit(x,y,4)
x=1:0.1:8;
y1=polyval(p,x);
hold on
plot(x,y1)
七次多项式拟合:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
plot(x,y,'.')
p=polyfit(x,y,7)
x=1:0.1:8;
y1=polyval(p,x);
hold on
plot(x,y1)
指数函数拟合:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
%lx=log(x);
ly=log(y);
plot(x,y,'.')
p=polyfit(x,ly,1)
y1=exp(p(2))*exp(p(1)*x);
hold on
plot(x,y1)
利用残差平方和一次多项式拟合:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
plot(x,y,'.')
p=polyfit(x,y,1)
y1=polyval(p,x);
hold on
plot(x,y1)
sum=0;
for i = 1:length(y)
sum = sum + (y(i)-y1(i))^2;
end
sum
利用残差平方和四次多项式拟合:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
plot(x,y,'.')
p=polyfit(x,y,4)
y1=polyval(p,x);
hold on
plot(x,y1)
sum=0;
for i = 1:length(y)
sum = sum + (y(i)-y1(i))^2;
end
sum
利用残差平方和七次多项式拟合:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
%lx=log(x);
ly=log(y);
plot(x,y,'.')
p=polyfit(x,ly,1)
y1=exp(p(2))*exp(p(1)*x);
hold on
plot(x,y1)
sum=0;
for i = 1:length(y)
sum = sum + (y(i)-y1(i))^2;
end
sum
利用残差平方和指数函数拟合:
clc
x=[1 1.5 3 4 5 6 6.5 7 8];
y=[1.2 1 1.7 2.5 2 2.3 2.5 3 3.1];
%lx=log(x);
ly=log(y);
plot(x,y,'.')
p=polyfit(x,ly,1)
y1=exp(p(2))*exp(p(1)*x);
hold on
plot(x,y1)
sum=0;
for i = 1:length(y)
sum = sum + (y(i)-y1(i))^2;
end
sum