▲

| 欧 式 空 间 | 第
1
篇 文 章 |
作者: Daniel

施密特正交化公式在用正交矩阵化二次型为标准形中有重要的应用。学过的同学都反映这个公式不太好记。本文用三幅图形教你记忆这个公式。
施密特正交化的定义
在n为欧式空间中,利用一组线性无关的向量

, 构造一组两两正交的单位向量组的过程叫做施密特正交化,它包括正交化和单位化两个步骤。
由于将一个向量化为单位向量很容易,只要除以它的长度即可,所以本文只谈正交化步骤。
三幅图形
一般的n维欧式空间中的施密特正交化公式与
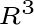
中的公式有相同的形式,所以,可以用
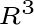
中公式的几何意义来帮助记忆此公式。
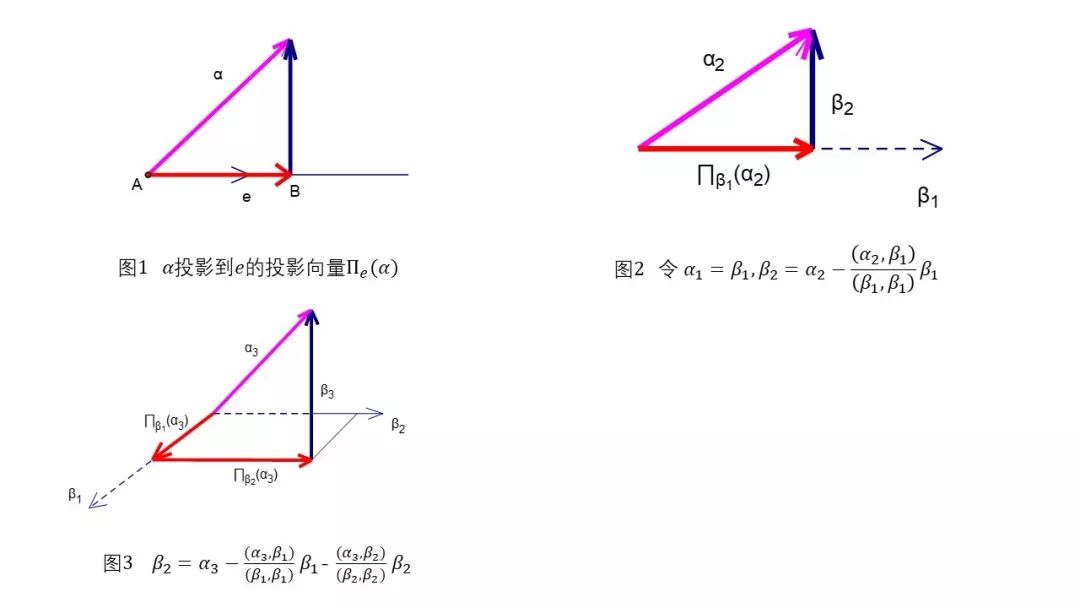
如图1,将向量
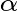
投影到向量
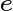
上的投影向量 ,记为
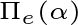
, 其公式在“投影向量计算公式的推导”一文中有详细介绍,请参阅。请大家先记住下面这个投影向量公式:
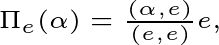
这里
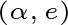
表示这两个向量的内积,在
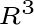
中就是点乘。
如图2,第一步:令
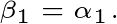
第二步:计算
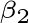
,使得
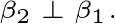
如图2, 取
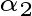
, 将它投影到
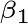
得到投影向量
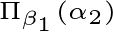
,即图中红色的水平向量,由图中的三角形法则知,
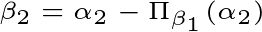
,就是与
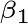
垂直的向量。于是,
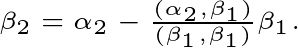
第三步:现在来求
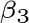
, 如图3, 将刚才求出的
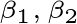
放在水平平面上,现在添加向量
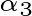
,它必不在水平平面上。图3告诉我们,用
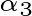
减去它分别向
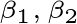
投影的投影向量得到
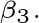
所以,
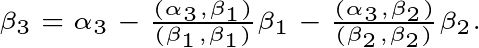
类比这个结构,当我们得到两两正交的向量组
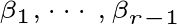
后,要求
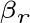
,使得它与前面的各
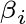
正交,只要添加向量
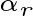
, 并用它减去它分别向
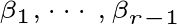
投影的投影向量
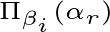
即得到
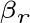
,所以,
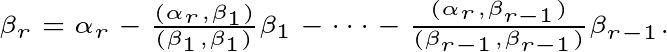
本文公式采用【upub编辑器】,请关注【编辑之谈】公众号!


-
投影向量计算公式的推导
-
矩阵特征多项式的系数公式
-
用正交变换将二次型化为标准形
-
复数集合作为复数域和实数域上的线性空间
-
生成子空间的交空间与和空间的求法
-
计算二次型的标准形的三种方法
▼

