JS中的数据结构
1、Queue 队列
JavaScript中没有队列这个数据结构,但是可以用数组来实现所有的功能。

队列是一个先进先出的数据结构,一般JavaScript中采用队列解决问题时会用到
-
入队push ()
:在数组的尾部添加元素 -
出队shift ()
:移除数组中第一个元素 -
queue (0)
:取数组的第一个元素 -
isEmpty ()
:确定队列是否为空 -
size ()
:获取队列中元素的数量
2、Stack 栈
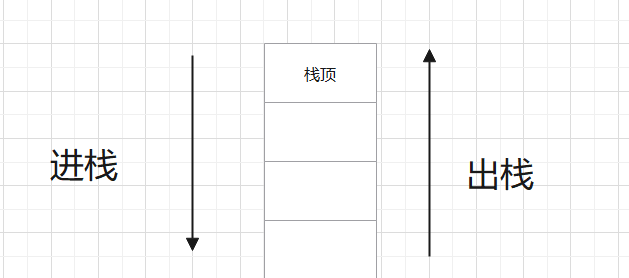
1️⃣栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。它按照
先进
⬇
后出
⬆的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。
2️⃣JavaScript中没有栈,但是可以用Array实现栈的功能。
3️⃣栈中数组长度减一即为栈尾元素,也就是最后进入的那个元素,最先出去的那个元素
JavaScript中对栈的操作一般会使用到
-
push()
方法,将元素压入栈顶 -
pop()
方法,从栈顶弹出(删除)元素,并返回该元素 -
peek()
方法,返回栈顶元素,不删除 -
clear()
方法,清空栈 -
length
拿到栈中元素数量
3、Linked List 链表
链表
是由多个元素组成的列表,链表中的元素储存不连续,用
next指针
连接在一起。
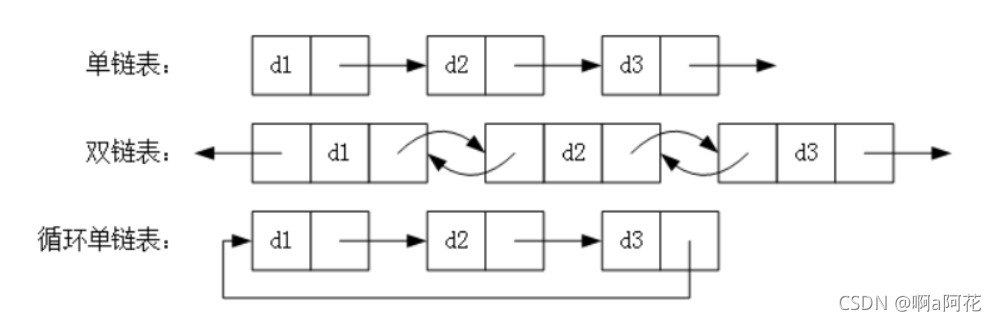
数组
:增删非数组元素需要移动元素
链表
:增删非首尾元素不需要移动元素只需要更改next的指向即可
链表是一个链式数据结构,每个节点由两个信息组成:节点的数据和指向下一个节点的指针。链表和传统数组都是线性数据结构,具有序列化的存储方式。
| 操作 | 数组 | 链表 |
|---|---|---|
| 内存分配 | 编译和序列化过程中静态分配 | 运行过程中动态分配 |
| 获取元素 | 从索引中读取 | 读取队列中的所有节点,直到特定元素,较慢 |
| 增加/删除元素 | 顺序增加删除,较慢 | 动态分配,内存消耗小,速度快 |
| 空间结构 | 一维或者多维 | 单边/多边,循环链表 |
JavaScript
中没有链表,但是可以用object来模拟链表
const a = { val: 'a' }
const b = { val: 'b' }
const c = { val: 'c' }
const d = { val: 'd' }
// a的next属性指向b
a.next = b;
b.next = c;
c.next = d;
// 这个嵌套的object就相当于一个链表
遍历链表
?遍历链表就是跟着链表从链表的
头元素
(head)一直走到
尾元素
(但是不包含链表的头节点,头通常用来作为链表的接入点)
?♂️还有一个问题,链表的尾元素指向一个
null
节点
// 声明一个指针,指向a
let p = a
// 当p还有值得时候
while (p) {
console.log(p.val)
// 不断得让p指向下一个位置
p = p.next
}
插入链表
// 在链表中插入值
const f = { val: 'f' }
c.next = f
f.next = d
删除链表
// 删除值
c.next = d
4、集合
集合
:一种无序且唯一的数据结构,集合区别队列、栈、链表最大的区别就是元素不能重复
JavaScript中ES6中新增了集合这种数据结构,可以通过实例化Set对象来创建集合
const set = new Set()
集合常用来解决的问题:
-
去重
set = new Set(arr)
,返回一个不含重复元素的集合 -
判断元素是否在集合中
set.has(num)
,判断num是否在集合中 -
求两个集合的交集
先将集合set1转换为数组,然后利用数组中的filter方法将set1在set2中的值返回,最后将返回的值转换为集合
const set1 = new Set([1,2,4])
const set2 = new Set([3,4])
const set3 = new Set([...set1].filter(item = > set2.has(item)))
//set3{4}
- 求两个集合的并集
const set1 = new Set([1,2,4])
const set2 = new Set([3,4])
let set3 = new Set([...set1, ...set2]);
// set3 {1, 2, 3, 4}
- 求两个集合的差集
const set1 = new Set([1,2,4])
const set2 = new Set([3,4])
let set3 = new Set([...set1].filter(x => !set2.has(x)));
// set3 {1,2}
filter() 方法创建一个新的数组,新数组返回指定数组中符合条件的所有元素
...
是ES6中新增的扩展运算符,对象中的扩展运算符(…)用于取出参数对象中的所有可遍历属性,拷贝到当前对象之中。
[...set]
的意思就是将集合转换为数组
5、树
前端?树结构还是比较常见的,例如级联选择、层级目录等都是树形结构。
javascript中没有树这个数据结构,但是一般用object和arrey来模拟树。
const tree = {
values:a,
children:[
{
values:b,
children:[
{
values:d,
children:[]
},
{
values:e,
children:[]
},{
values:f,
children:[]
}
]
},
{
values:c,
children:[
{
values:g,
children:[]
},
{
values:h,
children:[]
}
]
}
]
}
上面的代码模拟的就是下图的树结构
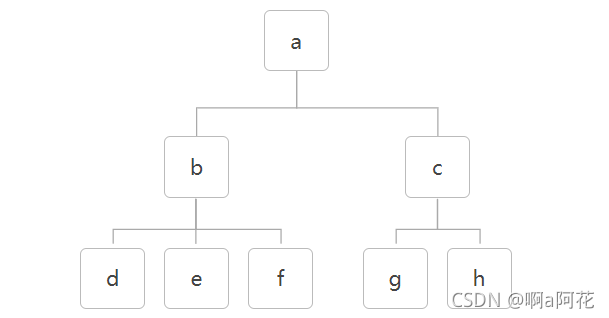
树的常用遍历方式
-
深度优先遍历
尽可能深的遍历树的分支。先访问根节点,然后再对子节点挨个使用深度优先遍历。
上图中的树使用深度优先遍历
const deepNood = (node)=>{
//打印根节点
console.log(node.values);
//遍历子节点
node.children.forEach(child => {
//递归
deepNood(child)
})
}
deepNood(tree)
//a b d e f c g h
-
广度优先遍历
优先访问距离根节点最近的节点。广度优先遍历需要使用到队列这个数据结构
- 新建一个队列,把根节点入队
- 将队头出队并访问
- 将队头的children顺序入队
- 重复第二步和第三步,直到队列为空
上面的树使用广度优先遍历
const breadth = (node)=>{
//将树加入队列(整个object对象,)
const arr = [node];
//队列是否为空
while(arr.length > 0){
//从队列中取出根节点
const val = arr.shift()
console.log(val.values)
//遍历子节点
for(let child of val.children){
//将子节点加入队列
arr.push(child)
}
// 打开console.log(arr),就能看出不断的将childern入队,然后再将队头取出
}
}
breadth(tree)
//a b c d e f g h
二叉树
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成
树的每个节点最多只能有两个子节点

js中自然也没有二叉树这个数据结构,一般还是用object对象来模拟二叉树
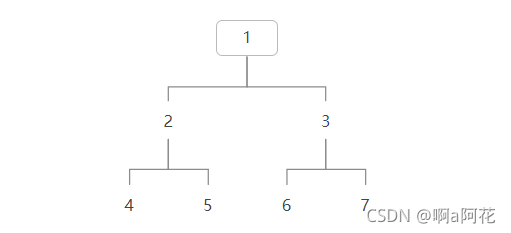
二叉树代码实现
const tree = {
val:1,
left:{
val:2,
left:{
val:4,
left:null,
right:null
},
right:{
val:5,
left:null,
right:null
}
},
right:{
val:3,
left:{
val:6,
left:null,
right:null
},
right:
{
val:7,
left:null,
right:null
}
}
}
二叉树遍历(递归)
(1)前序遍历
DLR
:根节点——左子树——右子树
每次遍历到一个节点都重复一次前序遍历
代码实现
const perorder = (node) =>{
//如果当前节点值为空则返回
if(!node) return;
//打印根节点
console.log(node.val);
//递归左子树
perorder(node.left);
//递归右子树
perorder(node.right);
}
perorder(tree)
//1 2 4 5 3 6 7
(2)中序遍历
LDR
:左子树——根节点——右子树
每次遍历到一个节点都重复一次中序遍历
代码实现
const perorder = (node) =>{
if(!node)return;
perorder(node.left);
console.log(node.val);
perorder(node.right);
}
perorder(tree)
//4 2 5 1 6 3 7
(3)后序遍历
LRD
:左子树——右子树——根节点
每次遍历到一个节点都重复一次后序遍历
代码实现
const perorder = (node) =>{
if(!node)return;
perorder(node.left);
perorder(node.right);
console.log(node.val);
}
perorder(tree)
//4 5 2 6 7 3 1
注意:
前序遍历第一个为根节点
中序遍历根节点左边为左子树,右边为右子树
后序遍历最后一个为根节点
6、堆
堆是一种特殊的完全二叉树
每层节点全部都填满,最后一层如果不是满的,只能缺少右边的节点,下图为最大堆的示例
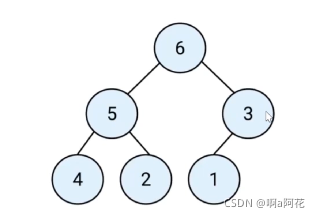
所有的节点都大于等于(最大堆)或者小于等于(最小堆)他的子节点
js中的堆
js中通常用数组来表示堆,按照广度优先的方式存储在数组中
根据广度优先的特点可以得到子节点在数组中的存储位置(index代表当前节点在数组中的下标)
左侧子节点的位置是2 * index+1
右侧子节点的位置是2 * index+1
父节点位置是(index – 1)/ 2
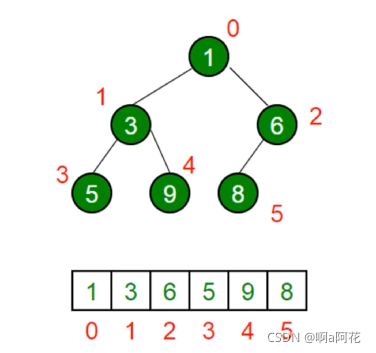
第k个最大元素
主要方法 :
插入元素
(最小堆)
构建一个最小堆,并将元素依次添加到堆中,
- 将值插入堆的底部,也就是数组的尾部
- 上移,将这个值与其父节点进行交换,直到父节点小于等于这个插入的值
- 大小为k的堆中插入元素的时间复杂度为O(logk)
删除堆顶
当堆的容量超过了k就删除堆顶
- 用数组尾部元素替换堆顶(直接删除堆顶会破坏堆解构)
- 下移,将新堆顶和子节点进行交换,直到子节点大于这个堆顶
- 大小为k的堆中删除堆顶的时间复杂度为O(logk)
获取堆顶
插入结束后堆顶就是第k个最大元素
获取堆大小
数组长度就是堆的大小
代码实现最小堆类
class minHeap{
constructor(){
this.heap = [];
}
// 获取父节点在数组中的下标
getParentIndex(i){
return Math.floor((i-1)/2)
//二进制写法
// return (i - 1) >> 1
}
// 获取左侧节点在数组中的下标
getLeftIndex(i){
return i * 2 + 1
}
// 获取右侧节点在数组中的下标
getRightIndex(i){
return i * 2 + 2
}
// 定义节点交换的方法
swap(i1,i2){
const temp = this.heap[i1];
this.heap[i1] = this.heap[i2];
this.heap[i2] = temp;
}
// 定义上移方法
shiftUp(index){
if(index==0){
return;
}
// 不停的和父节点交换位置,直到小于等于父节点的值
const parentIndex = this.getParentIndex(index)
if(this.heap[parentIndex] > this.heap[index]){
this.swap(parentIndex,index)
this.shiftUp(parentIndex)
}
}
// 定义下移方法
shiftDown(index){
const liftIndex = this.getLeftIndex(index)
const RightIndex = this.getRightIndex(index)
if(this.heap[liftIndex] < this.heap[index]){
this.swap(liftIndex,index)
this.shiftDown(liftIndex)
}
if(this.heap[RightIndex] < this.heap[index]){
this.swap(RightIndex,index)
this.shiftDown(RightIndex)
}
}
// 插入方法
insert (value){
// 将元素插入到数组的最后一位
this.heap.push(value)
// 因为插入的元素为数组的最后一位,所以传入的参数是heap.length-1
this.shiftUp(this.heap.length-1)
}
// 删除方法
delect(){
// pop可以删除数组的最后一个元素并返回这个元素
this.heap[0] = this.heap.pop();
this.shiftDown(0)
}
//获取堆顶
peek(){
return this.heap[0]
}
//获取堆大小
size(){
return this.heap.length
}
}
// 实例化一个最小堆
const h = new minHeap();
//插入几个数字测试
h.insert(3);
h.insert(2);
h.insert(1);
//虽然不能保证是按照最小堆来排列,但是能保证堆顶最小,也就是父节点的元素一定大于子节点的元素