支持向量机

支持向量机
0. 由来
1. 核心思想
2. 硬间隔支持向量机
- 2.1 间隔最大化
- 2.2 转换为拉格朗日对偶问题
  - 2.2.1 拉格朗日对偶问题
  - 2.2.2 将问题转换为拉格朗日对偶问题
3. 软间隔支持向量机
4. 泛函基础
5. 核支持向量机
- 5.1 正定核
- 5.2 常用核函数
  - 5.2.1 多项式核函数
  - 5.2.2 高斯核函数
    - 5.2.3 字符串核函数
6. SMO算法

0. 由来

Cortes与Vapnik 提出线性支持向量机.

Boser Guyon Vapnik 又引入核技巧，提出非线性支持向量机。

Vapnik：俄罗斯统计学家。

1. 核心思想

可以将数据分开的超平面有很多，SVM为了达到更好的泛化效果，寻找一个能正确划分数据且使支持向量（距离分类超平面最近的样本点）间隔最大的超平面。对于线性不可分数据，有两种处理方式：

松弛处理

：即允许分类器对部分样本的分类出错。
引入核函数

：通过核函数将输入特征空间变换到维度更高的隐特征空间，在维度更高的隐特征空间数据变得线性可分。

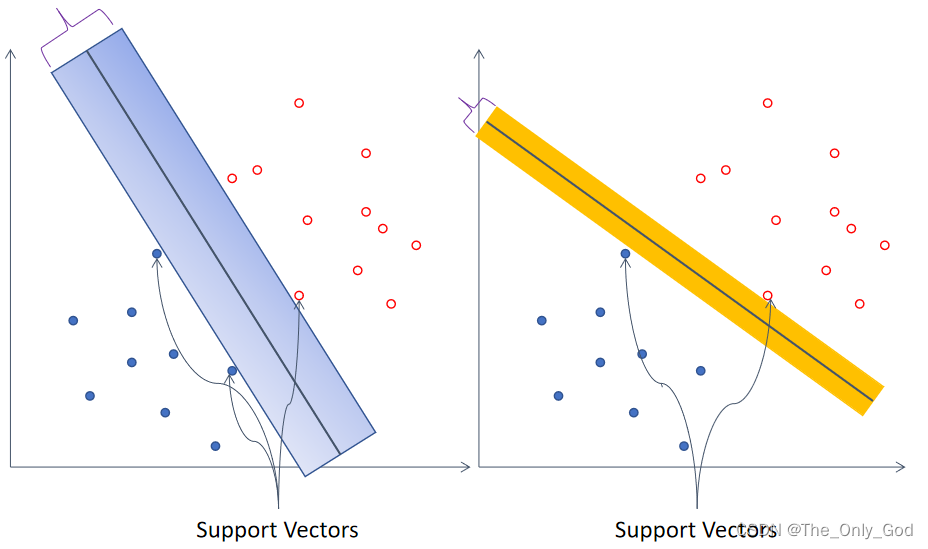
请添加图片描述

2. 硬间隔支持向量机

数据线性可分，寻找正确分类数据且间隔最大的超平面。

分类超平面：

∗

⋅

∗

w^*\cdot x+b^*=0

$w^{*} \cdot x + b^{*} = 0$

决策函数：

(

)

(

∗

⋅

∗

)

f(x)=sign(w^*\cdot x + b^*)

$f (x) = s i g n (w^{*} \cdot x + b^{*})$

2.1 间隔最大化

2.1.1 函数间隔

⋅

∣

|w\cdot x+b|

$∣ w \cdot x + b ∣$

能够相对的表示样本到超平面的距离，

⋅

w\cdot x+b

$w \cdot x + b$

的符号与

y

$y$

的符号是否一致可以表示分类是否正确，故可以定义函数间隔来表示分类的正确性和置信度：

(

⋅

)

min

⁡

1…

\hat \gamma_i = y_i(w\cdot x_i+b) \\ \hat \gamma = \min_{i=1…N}\hat \gamma_i

$\overset{γ}{^}_{i} = y_{i} (w \cdot x_{i} + b) \overset{γ}{^} = i = 1 . . . N min \overset{γ}{^}_{i}$

2.1.2 几何间隔

函数间隔存在一些问题：当

w

$w$

和

b

$b$

成比例的变化时，分类超平面没有改变但函数间隔确发生了变化，因此需要对

w

$w$

和

b

$b$

进行规范化，由此得出了几何间隔：

(

∥

⋅

∥

)

min

⁡

1…

\gamma_i = y_i(\frac{w}{\Vert w \Vert_2}\cdot x_i+\frac{b}{\Vert w \Vert_2}) \\ \gamma = \min_{i=1…N}\gamma_i

$γ_{i} = y_{i} (\frac{w}{∥ w ∥ _{2}} \cdot x_{i} + \frac{b}{∥ w ∥ _{2}}) γ = i = 1 . . . N min γ_{i}$

函数间隔和几何间隔存在如下关系：

∥

\gamma_i = \frac{\hat \gamma_i}{\Vert w \Vert_2}\\ \gamma = \frac{\hat \gamma}{\Vert w \Vert_2}

$γ_{i} = \frac{γ ^ _{i}}{∥ w ∥ _{2}} γ = \frac{γ ^}{∥ w ∥ _{2}}$

2.1.2 间隔最大化

确保分类正确的同时定义间隔最大化有：

⁡

∥

(

⋅

)

≥

\max_{w,b} \quad \frac{\hat \gamma}{\Vert w \Vert_2} \\ s.t. \quad y_i(w\cdot x_i+b)\ge \hat \gamma\\ \hat \gamma \ge 0

$w, b max \frac{γ ^}{∥ w ∥ _{2}} s . t . y_{i} (w \cdot x_{i} + b) \geq \overset{γ}{^} \overset{γ}{^} \geq 0$

函数间隔

\hat \gamma

$\overset{γ}{^}$

的取值并不影响最优化问题的解事实上，假设将

w,b

$w, b$

按比例改变为

\lambda w,\lambda b

$λ w, λ b$

这时函数间隔成为

\lambda \hat \gamma

$λ \overset{γ}{^}$

，不妨令

\hat \gamma=1

$\overset{γ}{^} = 1$

则有：

⁡

∥

(

⋅

)

≥

\min_{w,b} \quad \frac{1}{\Vert w \Vert_2} \\ s.t. \quad y_i(w\cdot x_i+b)\ge 1

$w, b min \frac{1}{∥ w ∥ _{2}} s . t . y_{i} (w \cdot x_{i} + b) \geq 1$

该问题的解具有存在性和唯一性，详细证明见李航《统计机器学习》

2.2 转换为拉格朗日对偶问题

2.2.1 拉格朗日对偶问题

对于含有不等式的约束问题：

⁡

(

)

(

)

≤

(

)

\begin{aligned} \min \quad f(x)&\\ s.t.\quad c_i(x)&\le 0 \\ h_j(j)&=0 \end{aligned}

$min f (x) s . t . c_{i} (x) h_{j} (j) \leq 0 = 0$

希望找到一个无约束优化问题，使得无约束优化问题的解即为原问题的解，由此构造了拉格朗日函数：

(

)

(

)

∑

(

)

∑

(

)

L(x,\alpha,\beta) = f(x)+\sum_i \alpha_i c_i(x)+\sum_j\beta_i h_j(x)\\

$L (x, α, β) = f (x) + i \sum α_{i} c_{i} (x) + j \sum β_{i} h_{j} (x)$

通过对

\alpha

$α$

加限制可以做到：

⁡

≥

(

)

(

)

(

)

≤

(

)

\begin{aligned} \quad \max_{\alpha\ge0,\beta}L(x,\alpha,\beta)&=f(x)\\ s.t.\quad c_i(x)&\le 0 \\ h_j(j)&=0 \end{aligned}

$α \geq 0, β max L (x, α, β) s . t . c_{i} (x) h_{j} (j) = f (x) \leq 0 = 0$

原始问题和对偶问题具有如下关系：

⁡

≥

min

⁡

(

)

≤

min

⁡

≥

max

⁡

(

)

\max_{\alpha,\beta:\alpha\ge0} \min_x L(x,\alpha,\beta) \le \min_{\alpha,\beta:\alpha\ge0}\max_x L(x,\alpha,\beta)

$α, β : α \geq 0 max x min L (x, α, β) \leq α, β : α \geq 0 min x max L (x, α, β)$

则原问题变为：

⁡

≥

min

⁡

(

)

(

)

≤

(

)

\begin{aligned} \quad \max_{\alpha\ge0,\beta}\min_x\quad L(x,\alpha,\beta)\\ s.t.\quad c_i(x)\le 0\\ h_j(j)=0 \end{aligned}

$α \geq 0, β max x min L (x, α, β) s . t . c_{i} (x) \leq 0 h_{j} (j) = 0$

某些情况下原始问题和对偶问题的最优值相等（详细证明需要对偶相关理论），不妨设满足这个最优值的解为

∗

)

(x^*,\alpha^*,\beta^*)

$(x^{*}, α^{*}, β^{*})$

，则有成立的充要条件，即KKT条件：

(

∗

)

≥

∗

(

)

(

)

≤

(

)

\nabla_xL(x^*,\alpha^*,\beta^*)=0\\ \alpha_i \ge 0\quad i=1,2,…,k\\ \alpha^*_i c_i(x)=0 \quad i=1,2,…,k\\ c_i(x)\le0\quad i=1,2,…,k\\ h_j(x)=0 \quad j=1,2,…,l

$\nabla_{x} L (x^{*}, α^{*}, β^{*}) = 0 α_{i} \geq 0 i = 1, 2, . . ., k α_{i}^{*} c_{i} (x) = 0 i = 1, 2, . . ., k c_{i} (x) \leq 0 i = 1, 2, . . ., k h_{j} (x) = 0 j = 1, 2, . . ., l$

其中

∗

(

)

\alpha^*_i c_i(x)=0

$α_{i}^{*} c_{i} (x) = 0$

为对偶互补条件

2.2.2 将问题转换为拉格朗日对偶问题

定义拉格朗日函数有：

(

)

∥

−

∑

(

⋅

)

∑

L(w,b,\alpha)=\frac{1}{2}\Vert w \Vert_2^2-\sum_i^N\alpha_i y_i(w\cdot x_i+b)+\sum_i^N\alpha_i

$L (w, b, α) = \frac{1}{2} ∥ w ∥_{2}^{2} - i \sum N α_{i} y_{i} (w \cdot x_{i} + b) + i \sum N α_{i}$

⁡

≥

min

⁡

(

)

\max_{\alpha:\alpha\ge0} \min_{w,b} L(w,b,\alpha)

$α : α \geq 0 max w, b min L (w, b, α)$

求解

⁡

(

)

\min_{w,b}L(w,b,,\alpha)

$min_{w, b} L (w, b,, α)$

有：

(

)

−

∑

∇

(

)

−

∑

得

：

∑

\nabla_w L(w,b,\alpha)=w-\sum_i^N\alpha_iy_ix_i=0\\ \nabla_b L(w,b,\alpha)= -\sum_i^N\alpha_iy_i=0\\ 得：\\ w=\sum_i^N\alpha_iy_ix_i\\ \sum_i^N\alpha_iy_i=0

$\nabla_{w} L (w, b, α) = w - i \sum N α_{i} y_{i} x_{i} = 0 \nabla_{b} L (w, b, α) = - i \sum N α_{i} y_{i} = 0 得： w = i \sum N α_{i} y_{i} x_{i} i \sum N α_{i} y_{i} = 0$

带原拉格朗日函数整理得：

(

)

−

∑

(

⋅

)

∑

L(w,b,\alpha)=-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_j y_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i\\

$L (w, b, α) = - \frac{1}{2} i = 1 \sum N j = 1 \sum N α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) + i = 1 \sum N α_{i}$

对偶问题有：

⁡

(

)

min

⁡

−

(

)

\max_{\alpha} L(w,b,\alpha)=\min_{\alpha}-L(w,b,\alpha)

$α max L (w, b, α) = α min - L (w, b, α)$

则最后需要求解得问题变为

：

⁡

∑

(

⋅

)

−

∑

≥

\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_j y_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i\\ s.t. \sum_{i=1}^{N}\alpha_i y_i=0 \\ \alpha_i \ge 0,\quad i=1,2,…,N

$α min \frac{1}{2} i = 1 \sum N j = 1 \sum N α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) - i = 1 \sum N α_{i} s . t . i = 1 \sum N α_{i} y_{i} = 0 α_{i} \geq 0, i = 1, 2, . . ., N$

求解出最优的

∗

(

∗

)

\alpha^*=(\alpha_1^*,\alpha_2^*,…,\alpha_N^*)^T

$α^{*} = (α_{1}^{*}, α_{2}^{*}, . . ., α_{N}^{*})^{T}$

，后有解：

∗

∑

∗

−

∑

∗

(

⋅

)

w^* = \sum_{i=1}^N\alpha_i^*y_ix_i\\ b^*=y_j-\sum_{i=1}^N\alpha_i^*y_i(x_i\cdot x_j)

$w^{*} = i = 1 \sum N α_{i}^{*} y_{i} x_{i} b^{*} = y_{j} - i = 1 \sum N α_{i}^{*} y_{i} (x_{i} \cdot x_{j})$

决策函数有：

(

)

(

∑

∗

(

⋅

)

∗

)

f(x)=sign(\sum_{i=1}^N\alpha_i^*y_i(x\cdot x_i)+b^*)

$f (x) = s i g n (i = 1 \sum N α_{i}^{*} y_{i} (x \cdot x_{i}) + b^{*})$

3. 软间隔支持向量机

对于线性不可分数据，某些样本不满足函数距离不小于1得条件，因此可以通过对每个样本引入一个松弛变量

≥

\xi_i \ge0

$ξ_{i} \geq 0$

来松弛约束，并引入一个惩罚系数

C

$C$

最小化所有松弛变量，则有如下软间隔得支持向量机问题：

∥

∣

∑

(

⋅

)

≥

−

≥

min \quad \frac{1}{2}\Vert w \vert_2^2+C\sum_i \xi_i\\ s.t. \quad y_i(w\cdot x_i+b)\ge 1-\xi_i,\quad i=1,2,…,N\\ \xi_i\ge 0, \quad i=1,2,…,N

$m i n \frac{1}{2} ∥ w ∣_{2}^{2} + C i \sum ξ_{i} s . t . y_{i} (w \cdot x_{i} + b) \geq 1 - ξ_{i}, i = 1, 2, . . ., N ξ_{i} \geq 0, i = 1, 2, . . ., N$

则此时拉格朗日函数有：

(

)

∥

∣

∑

−

∑

(

⋅

)

−

)

−

∑

L(w,b,\xi,\alpha,\mu)=\frac{1}{2}\Vert w \vert_2^2+C\sum_i \xi_i-\sum_i\alpha_i(y_i(w\cdot x_i+b)-1+\xi_i)-\sum_i\mu_i\xi_i

$L (w, b, ξ, α, μ) = \frac{1}{2} ∥ w ∣_{2}^{2} + C i \sum ξ_{i} - i \sum α_{i} (y_{i} (w \cdot x_{i} + b) - 1 + ξ_{i}) - i \sum μ_{i} ξ_{i}$

求解偏导数有：

(

)

−

∑

∇

(

)

−

∑

∇

(

)

−

\nabla_wL(w,b,\xi,\alpha,\mu)=w-\sum_i \alpha_i y_i x_i = 0\\ \nabla_bL(w,b,\xi,\alpha,\mu)= -\sum_i\alpha_iy_i=0\\ \nabla_{\xi_i} L(w,b,\xi,\alpha,\mu)= C-\alpha_i-\mu_i=0

$\nabla_{w} L (w, b, ξ, α, μ) = w - i \sum α_{i} y_{i} x_{i} = 0 \nabla_{b} L (w, b, ξ, α, μ) = - i \sum α_{i} y_{i} = 0 \nabla_{ξ_{i}} L (w, b, ξ, α, μ) = C - α_{i} - μ_{i} = 0$

解得：

∑

−

w=\sum_i \alpha_i y_i x_i\\ \sum_i\alpha_iy_i=0\\ C-\alpha_i-\xi_i=0

$w = i \sum α_{i} y_{i} x_{i} i \sum α_{i} y_{i} = 0 C - α_{i} - ξ_{i} = 0$

代入原问题得：

⁡

(

)

−

∑

(

⋅

)

∑

\min_{w,b,\xi}L(w,b,\alpha,\xi,\mu)=-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_j y_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i\\

$w, b, ξ min L (w, b, α, ξ, μ) = - \frac{1}{2} i = 1 \sum N j = 1 \sum N α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) + i = 1 \sum N α_{i}$

需要求解得对偶问题有：

⁡

≥

min

⁡

(

)

max

⁡

≥

−

∑

(

⋅

)

∑

−

≥

\max_{\alpha,\mu:\alpha\ge0,\mu\ge0} \min_{w,b,\xi} L(w,b,\alpha,\xi,\mu)\\ = \max_{\alpha,\mu:\alpha\ge0,\mu\ge0}-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_j y_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i\\ s.t.\quad \sum_i\alpha_iy_i=0\\ \quad C-\alpha_i-\mu_i=0\\ \quad \alpha_i\ge0\\ \quad \mu_i \ge 0

$α, μ : α \geq 0, μ \geq 0 max w, b, ξ min L (w, b, α, ξ, μ) = α, μ : α \geq 0, μ \geq 0 max - \frac{1}{2} i = 1 \sum N j = 1 \sum N α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) + i = 1 \sum N α_{i} s . t . i \sum α_{i} y_{i} = 0 C - α_{i} - μ_{i} = 0 α_{i} \geq 0 μ_{i} \geq 0$

合并约束条件，转为求最小目标，则有对偶问题：

⁡

≥

∑

(

⋅

)

−

∑

≤

\min_{\alpha:\alpha\ge0}\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_j y_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i\\ s.t.\quad \sum_i\alpha_iy_i=0\\ \quad 0\le\alpha_i\le C

$α : α \geq 0 min \frac{1}{2} i = 1 \sum N j = 1 \sum N α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) - i = 1 \sum N α_{i} s . t . i \sum α_{i} y_{i} = 0 0 \leq α_{i} \leq C$

4. 泛函基础

泛函分析形成于20世纪30年代，从变分问题、积分方程和理论物理得研究中发展而来，主要研究：

无限维向量空间上的函数、算子和极限理论；
拓扑线性空间到拓扑线性空间之间，满足各种拓扑和代数条件的映射。

算子：把无限维空间到无限维空间的变换。

4.1 度量（距离）空间

4.1.1 定义

设X是非空集合，对于

X

$X$

中的任意两元素

x

$x$

与

y

$y$

，按某一法则都对应唯一的实数

(

)

\rho(x,y)

$ρ (x, y)$

，并满足以下三条公理（距离公理）：

非负性：

(

x

,

y

)

≥

0

\rho(x,y)\ge 0

$ρ (x, y) \geq 0$

，

(

x

,

y

)

=

0

\rho(x,y)=0

$ρ (x, y) = 0$

当且仅当

=

y

x=y

$x = y$
对称性：

(

x

,

y

)

=

ρ

(

y

,

x

)

\rho(x,y) = \rho(y,x)

$ρ (x, y) = ρ (y, x)$
三角不等式: 对任意的

,

y

,

z

x,y,z

$x, y, z$

有：

(

x

,

y

)

≤

ρ

(

x

,

z

)

+

ρ

(

z

,

y

)

\rho(x,y)\le \rho(x,z) + \rho(z,y)

$ρ (x, y) \leq ρ (x, z) + ρ (z, y)$

则称：

(

)

\rho(x,y)

$ρ (x, y)$

为

x

$x$

与

y

$y$

间的距离（或度量）；

X

$X$

是以

\rho

$ρ$

为距离的距离空间（或度量空间），记成

)

(X,\rho)

$(X, ρ)$

，或简记为

X

$X$

；

X

$X$

中的元素称为

X

$X$

中的点。

点（元素）包含：真正意义下得点、数列和函数。
泛函分析是研究一个空间中点与点之间的关系，以及空间中符合一定条件的点组成的该空间子集的一些性质。

4.1.2
$\rho ρ 次幂可积函数空间$

[

]

L^p[a,b]

$L^{p} [a, b]$

表示区间

]

[a,b]

$[a, b]$

绝对值的

\rho

$ρ$

次幂

L

$L$

可积函数的全体，并把几乎处处相等的函数看成是同一个函数，对于

∈

[

]

x,y\in L^p[a,b]

$x, y \in L^{p} [a, b]$

，规定:

(

)

[

∫

∣

(

)

−

(

)

∣

]

≥

\rho(x,y)=\bigg[\int_a^b\big|x(t)-y(t)\big|dt\bigg]^\frac{1}{p},p\ge1

$ρ (x, y) = [\int_{a}^{b} ∣ ∣ x (t) - y (t) ∣ ∣ d t]^{\frac{1}{p}}, p \geq 1$

则

[

]

L^p[a,b]

$L^{p} [a, b]$

构成一个距离空间，称之为

\rho

$ρ$

次幂可积函数空间。

4.1.3 完备性概念

设

)

(X,\rho)

$(X, ρ)$

为度量空间：

设

x

n

}

n

=

1

∞

\{x_n\}_{n=1}^\infty

${x_{n}}_{n = 1}^{\infty}$

是

X

$X$

中的点列，如果对于任一正数

\epsilon

$ϵ$

,存在正数

N

$N$

，使得当自然数

,

m

≥

N

n,m\ge N

$n, m \geq N$

时：

(

x

n

,

x

m

)

<

ϵ

\rho(x_n,x_m)<\epsilon

$ρ (x_{n}, x_{m}) < ϵ$

就称

x

n

}

n

=

1

∞

\{x_n\}_{n=1}^\infty

${x_{n}}_{n = 1}^{\infty}$

是

X

$X$

中的基本点列，或者称为

a

u

c

h

y

Cauchy

$C a u c h y$

点列。
如果度量空间$ X

每

个

基

本

点

列

都

收

敛

，

称

中每个基本点列都收敛，称

$中每个基本点列都收敛，称$

X$是完备度量空间。

4.2 线性空间

空间中的任意两点可以做加法或与数相乘，运算的结果仍未该空间的点，并且该空间中的每个点可以定义长度，这个长度称为该点的范数，范数可以视为欧式空间中向量长度概念的推广。

4.3 赋范空间

设

X

$X$

是实（或复）线性空间，如果对于

X

$X$

中每个元素

x

$x$

，按照一定的法则对应于实数

∥

\Vert x\Vert

$∥ x ∥$

，且满足：

x

∥

≥

0

\Vert x\Vert \ge 0

$∥ x ∥ \geq 0$

，

x

∥

=

0

\Vert x\Vert =0

$∥ x ∥ = 0$

当且仅当

X

$X$

等于零元
a

x

∥

=

∣

a

∣

∥

x

∥

\Vert ax\Vert = |a|\Vert x\Vert

$∥ a x ∥ = ∣ a ∣ ∥ x ∥$

，

a

$a$

是实（或复）数
x

+

y

∥

≤

∥

x

∥

+

∥

y

∥

\Vert x+y\Vert\le\Vert x\Vert+\Vert y\Vert

$∥ x + y ∥ \leq ∥ x ∥ + ∥ y ∥$

则称

∥

\Vert X\Vert

$∥ X ∥$

是实（或复）赋范线性空间，

∥

\Vert x\Vert

$∥ x ∥$

称为

x

$x$

的范数

赋范线性空间必然是距离空间：定义

(

x

,

y

)

=

∥

x

−

y

∥

\rho(x,y)=\Vert x-y\Vert

$ρ (x, y) = ∥ x - y ∥$
与度量空间不同：
- 平移不变性：
  
  (
  
  x
  
  +
  
  a
  
  ,
  
  y
  
  +
  
  a
  
  )
  
  =
  
  d
  
  (
  
  x
  
  ,
  
  y
  
  )
  
  d(x+a,y+a)=d(x,y)
  
  $d (x + a, y + a) = d (x, y)$
  
  ,
  
  ,
  
  y
  
  ,
  
  a
  
  x,y,a
  
  $x, y, a$
  
  属于
  
  X
  
  $X$
- 齐次性：
  
  (
  
  a
  
  x
  
  ,
  
  a
  
  y
  
  )
  
  =
  
  ∣
  
  a
  
  ∣
  
  d
  
  (
  
  x
  
  ,
  
  y
  
  )
  
  d(ax,ay)=|a|d(x,y)
  
  $d (a x, a y) = ∣ a ∣ d (x, y)$
  
  ,
  
  ,
  
  y
  
  x,y
  
  $x, y$
  
  属于
  
  X
  
  $X$
  
  ，
  
  a
  
  $a$
  
  属于
  
  K
  
  $K$

4.4 巴拿赫（Banach）空间

如果赋范线性空间

∣

)

(X, ||.||)

$(X, ∣ ∣ . ∣ ∣)$

是完备的，则称(X, ||.||)是Banach空间。

例子：

n

$n$

维Euclid空间

n

R^n

$R^{n}$

是Banach空间
p

[

a

,

b

]

(

p

≥

1

)

L^p[a,b](p\ge1)

$L^{p} [a, b] (p \geq 1)$

是Banach空间

算子

：

T

$T$

是由赋范线性空间

X

$X$

中的某个子集

D

$D$

到赋范线性空间中的一个映射，则称

T

$T$

是算子，

D

$D$

是

T

$T$

的定义域，记为

(

)

D(T)

$D (T)$

，像集

∣

∈

}

\{y|y=Tx,x\in D\}

${y ∣ y = T x, x \in D}$

是

T

$T$

的值域，记为

(

)

T(D)

$T (D)$

。

线性算子：

T

$T$

满足可加性和齐次性

可加性：

(

x

+

y

)

=

T

x

+

T

y

T(x+y)=Tx+Ty

$T (x + y) = T x + T y$
齐次性：

(

a

x

)

=

a

T

(

x

)

T(ax)=aT(x)

$T (a x) = a T (x)$

**有界算子：**存在正数

M

$M$

使得对于一切

∈

(

)

x\in D(T)

$x \in D (T)$

，有

∥

≤

∥

\Vert Tx\Vert \le M\Vert x\Vert

$∥ T x ∥ \leq M ∥ x ∥$

4.5 内积空间

设X 是定义在实（或复）数域

K

$K$

上的线性空间，若对于

X

$X$

任意一对有序元素

x,y

$x, y$

, 恒对应数域

K

$K$

的值

)

(x,y)

$(x, y)$

，且满足：

a

x

,

y

)

=

a

(

x

,

y

)

(ax,y)=a(x,y)

$(a x, y) = a (x, y)$
x

+

y

,

z

)

=

(

x

,

z

)

+

(

y

,

z

)

(x+y,z)=(x,z)+(y,z)

$(x + y, z) = (x, z) + (y, z)$
x

,

y

)

=

(

y

,

z

)

(x,y)=(y,z)

$(x, y) = (y, z)$
x

,

x

)

≥

0

(x,x)\ge0

$(x, x) \geq 0$

，且

x

,

x

)

=

0

(x,x)=0

$(x, x) = 0$

的充要条件是

=

0

x=0

$x = 0$

则称

X

$X$

为内积空间，

)

(x,y)

$(x, y)$

称为

x,y

$x, y$

的内积。

4.6 希尔伯特(Hibert)空间

可由内积导出范数：

∥

(

)

\Vert x\Vert = \sqrt{(x,x)}

$∥ x ∥ = (x, x)$

完备的内积空间称为希尔伯特空间。

5. 核支持向量机

通过一个非线性变换将输入空间(欧氏空间

R

$R$

或离散集合)对应于一个特征空间(希尔伯特空间)，使得在输入空间中的超曲面模型对应于特征空间中的超平面模型(支持向量机)。

(

)

(

)

⋅

(

)

K(x,z)=\phi(x)\cdot\phi(z)

$K (x, z) = ϕ (x) \cdot ϕ (z)$

其中

(

)

K(x,z)

$K (x, z)$

为核函数，

(

)

\phi(x)

$ϕ (x)$

为映射函数。

在学习与预测中只定义核函数

则核支持向量机的目标函数有：

(

)

∑

(

)

−

∑

W(\alpha)=\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_i\alpha_i\\

$W (α) = \frac{1}{2} i \sum j \sum α_{i} α_{j} y_{i} y_{j} K (x_{i}, x_{j}) - i \sum α_{i}$

核支持向量机要求解的问题：

⁡

∑

(

)

−

∑

≤

\min_\alpha\quad\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_i\alpha_i\\ s.t. \quad \sum_{i=1}^N\alpha_iy_i=0\\ \quad 0\le\alpha_i \le C,\quad i=1,2,…,N

$α min \frac{1}{2} i \sum j \sum α_{i} α_{j} y_{i} y_{j} K (x_{i}, x_{j}) - i \sum α_{i} s . t . i = 1 \sum N α_{i} y_{i} = 0 0 \leq α_{i} \leq C, i = 1, 2, . . ., N$

决策函数：

(

)

(

∑

∗

(

)

∗

)

f(x)=sign\bigg(\sum_i\alpha_i^*y_iK(x_i,x)+b^*\bigg)

$f (x) = s i g n (i \sum α_{i}^{*} y_{i} K (x_{i}, x) + b^{*})$

5.1 正定核

5.2 常用核函数

5.2.1 多项式核函数

(

)

(

⋅

)

K(x,z)=(x\cdot z+1)^p

$K (x, z) = (x \cdot z + 1)^{p}$

对应的支持向量机为P次多项式分类器

5.2.2 高斯核函数

(

)

(

−

∥

−

∥

)

K(x,z)=exp(-\frac{\Vert x-z\Vert^2}{2\sigma})

$K (x, z) = e x p (- \frac{∥ x - z ∥ ^{2}}{2 σ})$

高斯核函数对应的映射函数可以将数据映射到无限维

5.2.3 字符串核函数

6. SMO算法

序列最小优化算法

求解如下问题：

⁡

∑

(

)

−

∑

≤

是一种启发式算法，加快求解多变量约束问题

如果所有变量的解都满足此最优化问题的KKT条件，那么得到解；
否则，选择两个变量，固定其它变量，针对这两个变量构建一个二次规划问题，称为子问题，可通过解析方法求解，提高了计算速度。子问题的两个变量：一个是违反KKT条件最严重的那个，另一个由约束条件自动确定。

步骤：

求解两个变量的子问题二次规划问题
启发式寻找子问题的两个变量
继续执行1

参考资料

《统计机器学习》李航

https://baike.baidu.com/item/弗拉基米尔·万普尼克?fr=aladdin

https://blog.pluskid.org/archives/702

原文链接：https://blog.csdn.net/The_Only_God/article/details/128007827

目录