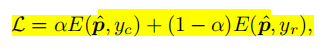本文作者为了解决数据长尾的问题,作者提出了BBN模型,该模型分成两个分支,一个是传统的学习分支,另一个是数据再平衡分支。这两个分支利用参数
进行平衡,
是根据训练的epochs的数量进行调整,它自适应调整整个模型,让模型首先关注传统的学习分支,之后逐渐关注数据再平衡分支。
数据平衡的一般策略
:
- 再采样方法:该方法是数据平衡中的主要方式,可以分为两类:1.对于拥有大部分数据的类别进行降采样;2.对拥有小部分数据的类别进行过采样。
- 权重再调整:该方法是另一个数据平衡的重要方法,它的策略是分配大的权重给小的类别在损失函数中。然而在真实数据应用时该方法会导致优化困难。
- 两步调节策略:该方法是把训练过程分为两部分,第一步用原始不平衡的数据训练模型,第二步用很小的学习率和平衡后的数据微调模型。
BBN模型
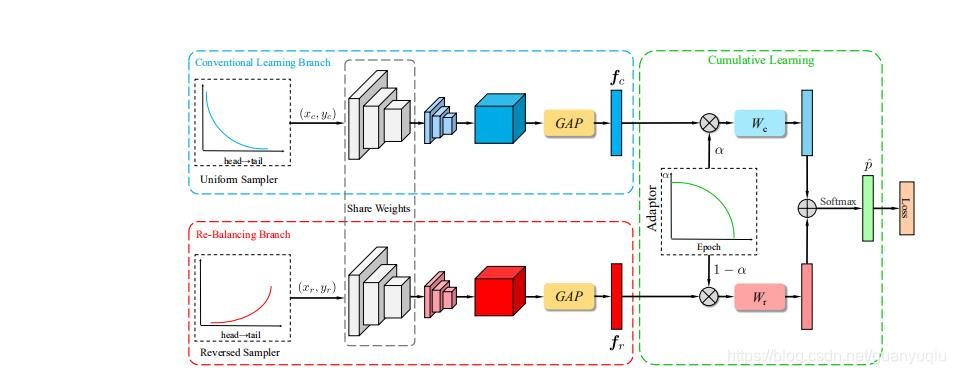
如上图所示,文中提出的BBN模型包含两个分支,分别是传统学习和对数据再平衡学习。其中传统学习分支输入的是正常的数据分布,而再平衡分支则使用reversed sampler,即与每个类别样本数量成反比例关系的采样策略。每个样本的采样概率为:

其中
![]()
两个分支共享除了最后模块的所有权重,为了在训练阶段平衡两个分支。用自适应权衡参数
来平衡两个分支,
采用自适应渐进式学习策略来进行调节,调节的方式是根据训练的epoch的数量调节,随着epoch的次数增多,
的值减少,在inference阶段,
设置为0.5,
的调节公式如下:
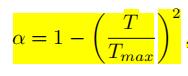
两个分支的权重是
和
,权重
和
将要被送到分类器
和
中,则输出的结果是这些权重的和,输出的结果可以表示为:
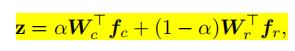
其中
是预测的输出,对于每一个类别
,损失函数的类别预测概率为:
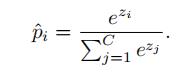
文中用
作为计算交叉熵损失函数,则输出的概率分布为
,BBN模型权重交叉熵损失可以写为: