Y. Chen, J. Sun, Y. Lin, G. Gui and H. Sari, “Hybrid n-Inception-LSTM-based aircraft coordinate prediction method for secure air traffic,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 3, pp. 2773-2783, Mar. 2022, doi: 10.1109/TITS.2021.3095129.(
Impact factors: 9.6
)
航空大数据专题已经更新完毕,欢迎读者交流。上方为已发表论文,含有该专题的更多细节。
第一章:
项目背景及数据集分析
第二章:
神经网络输入/输出数据集制作
第三章:
N-Inception-LSTM新型网络
第四章:
项目资源汇总及开源
目录
引言
重新回顾一下出发点,由于具体报文信息易被篡改,本文希望找到一种不受ADS-B具体报文信息影响的飞机坐标定位方案。如飞机失事,需要紧急救援,若报文被篡改,那么根据报文信息得到的坐标就是虚假的,无法实施及时救援,后果不堪设想。
那么在此整理一下,哪些信息是无法被篡改的呢?根据
航空大数据——由ADS-B报文系统预测飞机坐标(飞行轨迹)(一)
,在本文所用数据集中,
ADS-B信号强度、接收机本身序列号(Serial)、接收机本身坐标
是不易被篡改的。
ADS-B信号强度
:指接收机接收到的ADS-B信号强度,这是客观的,是由接收机在本地接收时测得的一个信息,不易被篡改。
接收机本身序列号(Serial)、接收机本身坐标
:这两个信息均能在前文所提的传感器数据集中找到,这些信息都是公开的,也不易被篡改。
根据前文分析,飞机与接收机距离越近,接收机接收到的ADS-B信号强度越大,而飞机与接收机距离涉及接收机本身坐标,又接收机序列号与坐标对等(已知序列号能知道坐标,已知坐标能找到序列号),因此从ADS-B信号强度、接收机本身序列号与坐标理论上能够挖掘出飞机发送ADS-B报文时的坐标。
输入/输出数据集制作
理论支持
1、单一时间点的输入/输出特征说明

图1
单一时间点的输入
/
输出数据
根据引言分析,得到如图
1
所示的单一时间点的输入
/
输出数据(后文所用模型的输入
/
输出为多个连续单一时间点的数据拼接),输入特征为
3
个地面传感器的序列号、接收信号强度和自身坐标,即每个传感器对应5
个特征,
因此输入的特征共计
15
个。输出特征为飞机的纬度和经度共计2
个特征。
若当前时间点接收到信号的地面传感器个数不足3个,则用0补充特征;若超过3个,则以前一章所述的各类传感器精度为优先级,挑选出3个优先级高的传感器作为特征使用。
2、连续时间戳分割

图2
时间戳分割(以采样时间步长等于
64
为例)
飞机坐标在时间上是连续的,为充分利用数据的时间特性,本文将数据集进行了连续时间戳分割,以采样时间步长等于
64
为例的数据采样过程如图
2
所示。先将数据集按航班号进行排列,再将每个航班的数据按服务器接收时间戳依次排列,图
2
左侧
Input
部分即两次排列后的效果图。
采样过程中用
64×15
的滑块在同一航班号内依次采样(其中
64表示连续时间点的个数,15表示单一时间点的特征个数
),滑块每次滑动步长为
1
,采样过程仅在单个航班内部采样,如:
sample2若再向下滑动一步,就同时包含了航班X和航班Y的信息了,此时需要直接跳到sample3的位置继续采样。
采样后得到输入样本集的维度为(
None
,
64
,15
),其中
None表示样本个数。同理,可以得到输出样本集的维度为(
None
,
64
)。
需要注意的是
,输出样本集的维度为(
None
,
64),不是(
None
,
64,1
),也不是(None
,
64
,2
)。
为什么不是(None,64,1)?
:(None,64,1)与(
None
,64)从矩阵内部数据上讲是等价的,只不过前者是三维矩阵,后者是二维矩阵。在神经网络运算中,对于三维矩阵需要用到二维卷积,而对于二维矩阵只需用到一维卷积,因此在不影响数据内容的前提下,将数据降维能够减少后续运算量。
为什么不是(None
,
64
,2
)?
:在后文神经网络中是对飞机坐标的经度和纬度进行了单独训练,即每次训练只有1个特征输出,而非2个特征。经实验论证,单独训练的性能优于经纬度同时训练的性能,实验数据不在此公开,直接公布结论。
3、样本数据归一化
在将样本数据输入到网络模型之前,需要对样本数据进行归一化,本文采用了最大最小归一化方法,具体的公式定义如下:
(1)
其中,
X
为原始样本数据,
max
为样本的最大值,
min
为样本的最小值,
N
为归一化后的样本。
这是一个很经典归一化方法,公式本身没有问题,但在对坐标归一化时
需要注意
,本文所用数据集多数为欧洲航班的信息,但不排除个别航班在欧洲之外,比如:大多数航班或传感器坐标纬度范围为36°~71°,有个别坐标的纬度在80°附近,又有个别坐标的纬度在10°附近,那么此时最大最小值不能选80°和10°,而应该选71°和36°。即
不能对数据集直接套函数归一化,需要对每一列数据进行升序或者降序排列,观察数据特征后手动设定最大和最小值
。
4、样本随机化

图3 样本随
机化
如图
3
所示,在样本数据归一化后还需要对样本数据进行打乱(
Shuffle
)操作,该操作能够增加样本随机性,防止模型在训练过程中的抖动,防止过拟合。实验结果表明,样本随机化后的性能会有提升。
代码实现
根据上一章所述,主数据集和传感器数据集被整合到了变量allinfo中,根据
单一时间点的输入/输出特征说明
,从allinfo中取出对应的15列输入特征并按列归一化,命名为x_train_norm,同理,取出对应的2列输出特征并按列归一化,命名为y_train_norm。
其中归一化及反归一化matlab代码如下:
补充说明:同一个项目中,所有的训练集和测试集需要用相同的归一化因子,归一化因子获取于项目中数据集初次归一化时,之后的归一化均用初次归一化时的因子。在对预测结果反归一化时,也需要用到归一化时的因子,因此,这个因子记得提前保存好。
% 归一化
x=从allinfo中取出的15列
x=x.'; % 先转置,归一按行归一
[x,ps_x_to01]=mapminmax(x,0,1); % ps为归一化因子
% x=mapminmax('apply',x,ps_x_to01); % 归一化时指定归一化因子
x_train_norm=x.';
y=从allinfo中取出的2列
y=y.';
[y,ps_y_to01]=mapminmax(y,0,1);
% y=mapminmax('apply',y,ps_y_to01);
y_train_norm=y.';
% 反归一
y=yla_pre;
y(:,2)=ylong_pre;
y=y.';
y=mapminmax('reverse',y,ps_y_to01); % 用归一化时的归一化因子,进行反归一化
y_pre=y.';
此处提供现成的归一化后的资源
,可以直接用来做后续步骤,内含4个归一化后的数据集和它们的归一化因子,可以根据需要制作成训练集、验证集或者测试集(
自己按照前面的步骤一步步做,也能得到相同的数据集
):
航空大数据:由ADS-B报文系统预测飞机坐标(飞行轨迹)配套资源-数据集文档类资源-CSDN文库
归一化后,输入和输出数据集制作matlab代码如下:
[n,m]=size(x_train_norm);
height=64;%连续时间点采样步长,根据需求可变
width=15;%单一时间点输入特征个数
index_3d=1;
i=1;
while i <= n%第一次遍历,确定根据当前矩阵x_train_norm能制作出多少个二维样本
if i+height-1 > n
break;
end
%保证采样窗里只有单个航班的信息
if x_train_norm(i,1) == x_train_norm(i+height-1,1)
index_3d=index_3d+1;
i = i+1;
continue;
end
%若采样窗里不是单个航班,则将窗口跳跃至下一个航班起始位置
for t = 1:height-1
if x_train_norm(i,1) ~= x_train_norm(i+t,1)
i=i+t;
break;
end
end
end
fprintf('total %d \n',index_3d-1);
%提前开辟空间,加快后续运算速度
x_train=zeros(index_3d-1,height,width);
yla_train=zeros(index_3d-1,height);
ylong_train=zeros(index_3d-1,height);
%(index_3d-1)是能够制作的样本数,生成一个1~(index_3d-1)的整数随机序列,用于实现shuffle操作。
% ps:这段代码是灵魂~~~~
randIndex = randperm(index_3d-1);
randIndex=randIndex.';
index_3d=1;
i=1;
%%%%%%%%%%%%%%%%%%%%%
% 在制作测试集时打开注释
% count=0;
% count_all_test=0;
% count_single_test=[];
%%%%%%%%%%%%%%%%%%%%%
while i <= n%第二次遍历,制作训练集
if(~mod(i,1000))
fprintf('已完成 %d 行转换!\n',i);
end
if i+height-1 > n
%%%%%% 在制作测试集时打开注释 %%%%%
% count=i-n-1;
% count_single_test=[count_single_test count];
% count_all_test=count_all_test+1;
% count=0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
break;
end
if x_train_norm(i,1) == x_train_norm(i+height-1,1)
index=randIndex(index_3d);%获取一个随机索引(灵魂~~~~)
% 若是在制作测试集,测试集不需要shuffle,测试集打乱后会增加后续维度复原难度
% 在制作测试集时直接按顺序将index作为索引即可,无需使用随机索引
% 即,制作测试集时,改为index=index_3d;
% 最终得到训练集输入x_train,和训练集输出yla_train、ylong_train
x_train(index,:,:)=x_train_norm(i:i+height-1,2:2+width-1);
yla_train(index,:)=y_train_norm(i:i+height-1,1);
ylong_train(index,:)=y_train_norm(i:i+height-1,2);
index_3d=index_3d+1;
i = i+1;
%%%%%% 在制作测试集时打开注释 %%%%%
% count=count+1;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
continue;
end
for t = 1:height-1
if x_train_norm(i,1) ~= x_train_norm(i+t,1)
i=i+t;
%%%%%% 在制作测试集时打开注释 %%%%%
% if count==0
% count=-t;
% end
% count_single_test=[count_single_test count];
% count_all_test=count_all_test+1;
% count=0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
break;
end
end
end
最终得到训练集输入
x_train
,和训练集输出
yla_train
、
ylong_train
。这样得到的数据集可以直接供后面神经网络使用,
验证集和测试集也可以用以上同样的方式制作而成
。
在制作测试集时,需要额外记录两个变量:
count_all_test
:记录了数据集中所有不同航班的航班数。
count_single_test
:记录了数据集中每一个航班在当前采样窗下所制成的样本数。
这两个变量主要是用于对测试集输出的维度还原,记得在制作测试集后保存。
输出维度还原
对测试集或实际预测时(训练集和验证集无需考虑维度还原),根据上述在制作输入数据集时对采样的描述,对于输出数据集理应能够被拆分成如图4所示的形式(意会一下~),即每一个航班的坐标(经度或纬度),连续时间采样的中间部分是被多次预测的,最后进行维度还原时需要根据重复预测次数取平均。
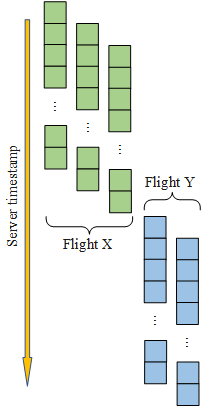
图4 输出拆解
matlab实现代码如下:
load('count_all_test.mat');
load('count_single_test.mat');%加载制作测试集输入时生成的变量count_all_test和count_single_test
yla=zeros(6000000,1);%预分配空间,用于存放降维后的数据
ylong=zeros(6000000,1);
len_y=1;%表示yla\ylong的index
y1=yla_pre.';%yla_pre和ylong_pre即为原始输出的预测坐标
y2=ylong_pre.';%ylong_pre按行排放,转成按列排
y_count=0;%表示y1\y2的index
size=64;%采样窗长度
count=0;%count为当前航班的样本数
for t = 1:count_all_test
fprintf("t=%d\n",t);
count=count_single_test(1,t);%count为当前航班的样本数
temp1=zeros(10000,10000);
temp2=zeros(10000,10000);
y_1=zeros(10000,1);
y_2=zeros(10000,1);%预分配空间,加速
if count<0%小于零表示采样时由于长度小于采样窗长度,没有被采到,所以在恢复时补nan
count=abs(count);
y_=nan(count,1);
yla(len_y:len_y+count-1,1)=y_;
ylong(len_y:len_y+count-1,1)=y_;
len_y=len_y+count;
continue;
end
%将同航班数据分解并排入同一个矩阵,方便求平均
for i = 1:count
temp1(i:i+size-1,i)=y1(:,i+y_count);
temp2(i:i+size-1,i)=y2(:,i+y_count);
end
y_count=y_count+count;
%按行求和
y_1=sum(temp1,2);
y_2=sum(temp2,2);
len=count+size-1;
%按行求平均
for i = 1:len
if i<size
y_1(i,1)=y_1(i,1)/i;
y_2(i,1)=y_2(i,1)/i;
%如果觉得前段和后段预测重复次数太少,可以选择抛弃数据
% y_1(i,1)=nan;
% y_2(i,1)=nan;
elseif i>len-size+1
y_1(i,1)=y_1(i,1)/(len-i+1);
y_2(i,1)=y_2(i,1)/(len-i+1);
% y_1(i,1)=nan;
% y_2(i,1)=nan;
else
%对重复预测次数最多的中间段取平均
y_1(i,1)=y_1(i,1)/size;
y_2(i,1)=y_2(i,1)/size;
end
end
yla(len_y:len_y+len-1,1)=y_1(1:len,1);
ylong(len_y:len_y+len-1,1)=y_2(1:len,1);
len_y=len_y+len;
end
最终得到变量
yla
和
ylong
,
对其用训练集的归一化因子进行返归一化(见上面归一化时的代码)
,即可得到神经网络对应每个输入时间点的预测坐标(经度和纬度)。
本章总结
本章主要介绍了如何制作适用于神经网络的数据集,为了利用数据中的时间特性,本文对原始数据集进行了按时间采样,后续实验表明利用时间特性相比直接使用原始数据,性能有着显著提升。对输入数据的时间采样,为输出数据复原制造了困难。