Matlab实现二维数字图像相关（2D Digital Image Correlation, 2D-DIC）【ADIC2D代码复现及原理介绍】

前言

由于本人近期正在展开数字图像相关技术用于测量材料形变方向的研究，其中需要对别人现有算法的复现和调研，尽管其中很多算法都已经非常成熟，但对于初学者而言即使明白其中的原理，无法上手实践和操作的话，依然无法能够将其完全的应用起来或者在上面进行创新，我希望能将自己作为一个初学者复现他人代码和学习该原理的过程记录下来，方便每一个涉足该领域的人能更快应用这些知识。

本文所复现的论文——

Atkinson D, Becker T. A 117 Line 2D Digital Image Correlation Code Written in MATLAB[J]. Remote Sensing, 2020, 12(18): 2906.

¹

GitHub源码地址：

https://github.com/SUMatEng/ADIC2D.git

由于官方数据集可能存在变动或者被墙，这里提供一下我已经上传好的版本

数据集地址：

百度云

：链接：

https://pan.baidu.com/s/1In4ZAFRIzfWIxoBSMAYGYQ

提取码：8xmi
谷歌云盘

：

https://drive.google.com/file/d/1JUTGmZirxXHYg4fPno-wE3YUmyTqWKzI/view?usp=sharing

数字图像相关专栏目录：

这篇论文是让我真正想要将自己正在做的这些事进行记录的源动力，因为这篇文章的作者也是考虑到尽管数字图像相关技术很成熟，但是网络上缺乏可以实操的源码便于理解，从而将简化的代码以及对于原理的解释共享在网络上便于他人学习。非常感谢Devan Atkinson，Thorsten Becker两位作者对于他们知识成果的共享。我将在这里将我学到的东西以中文的形式以方便国内的学者进行进一步的研究。

This paper aims to bridge the gap between the theory and implementation of DIC. It does this by firstly presenting the theory for a 2D, subset based DiC framework that is predominantly consistent with current state-of-the-art practices.
¹

一.数字图像相关（Digital Image Correlation）

数字图像相关技术(Digital Image Correlation, DIC)

是广泛应用于刚体结构形变检测的视觉测量技术。它通过在被测物表面投影或绘制随机散斑图案，定义图像的相似度函数，对物体形变前后的两幅图像进行分析即可得到采样点的位移场，从而得到形变
²
。数字图像相关技术按照其测量的维数，可以被分为

二维数字图像相关（Two-Dimensional Digital Image Correlation, 2D-DIC）

和

三维数字图像相关（Three-Dimensional Digital Image Correlation, 3D-DIC）

³
。如图所示
⁴
就是2D-DIC获取形变后子区位移场的过程。

a)参考图像及其子区 b)形变图像及其子区 c)相关运算后得到的位移场

对于数字图像相关而言，其流程可以分为标定、相关运算、位移变换以及最后根据实际需要计算应变或者其他信息四个步骤，标定就是通过一系列拍摄的特定图案的图片，利用标定算法求解出相机图像坐标系与真实世界坐标系下的映射关系，之后我单独写一篇来分享好了，这里主要分享一下相关运算的流程与推导。

二.相关运算

数字图像相关的本质就是在参考图像上设置好子区后，找到形变后图片上对应的已经产生过位移的子区，从而计算出形变子区相对于参考子区在图像坐标系上的位移，最终利用标定好的映射关系求解出该区域在实际物理空间中的位移，最后利用得到的位移计算得到所拍摄表面所发生的形变。

在这个过程中参考子区是已知的，但形变后的图片上原本的子区必然发生了变化，其具体位置是未知的，因此如何才能找到和原先参考子区对应的那块区域（求解这一未知量）正是关键所在，这正是相关运算所做的事情。

1.数学模型

我强烈建议大家能一起推导一次这一部分，对于理解相关运算有很大的作用！！

首先设

参考图像

为

F

$F$

，它很多时候代表了

t=0

$t = 0$

时刻所拍摄到的散斑图案，其上的

参考子区

设为

f

$f$

。

子区的排布有很多种，可以加步进那样整列排布，也可以随机的点选；子区的形状也可以各种各样，矩形、圆型，只要保证相关运算所处理的所有子区为同一种形状、大小的即可。

接下来设

形变图像

为

G

$G$

，其上的

形变子区

为

g

$g$

，如下为一个在相机图像坐标系下的示意图
¹

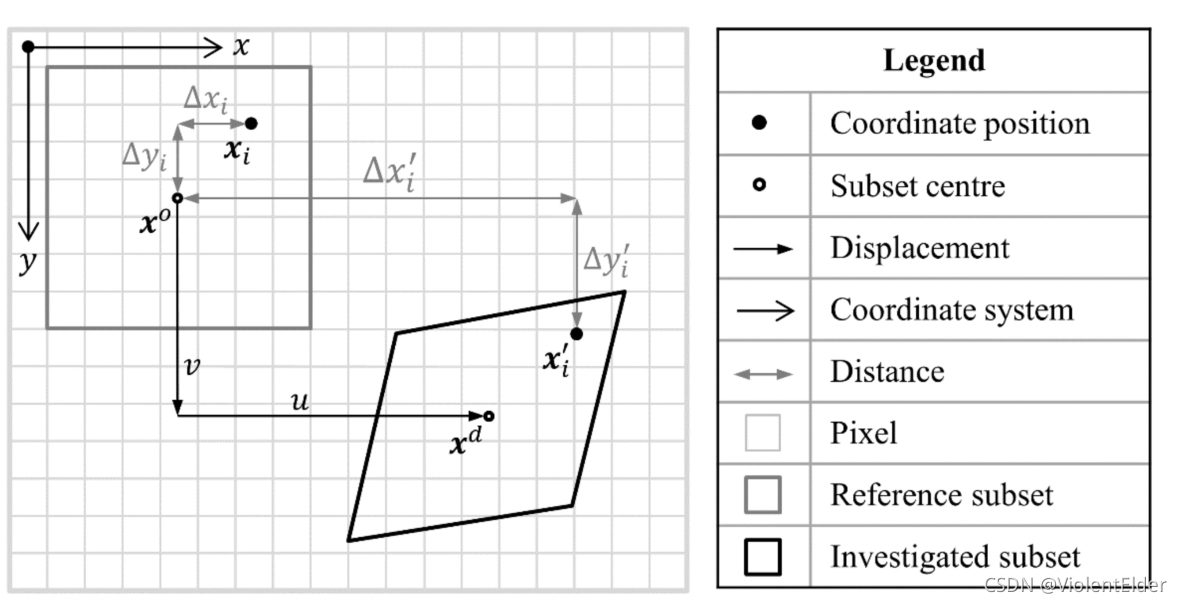
在这里插入图片描述

图中左上角的矩形框即为参考子区，右下角的平行四边形即为形变子区，其中参考子区

f

$f$

中心点为

[

]

\boldsymbol{x}^{0}=\left[\begin{array}{ll}x_{0} & y_{0}\end{array}\right]^{T}

$x^{0} = [x_{0} y_{0}]^{T}$

（后面的公式表达请注意上下标）

，参考子区上的其他像素点为

[

]

\boldsymbol{x}^{i}=\left[\begin{array}{ll}x_{i} & y_{i}\end{array}\right]^{T}

$x^{i} = [x_{i} y_{i}]^{T}$

。以中心点

\boldsymbol{x}^{0}

$x^{0}$

作为参考，我们可以得到

[

]

[

]

[

]

\boldsymbol{x}^{i}=\Delta \boldsymbol{x}^{i} \boldsymbol{x}^{0}+\boldsymbol{x}^{o}=\left[\begin{array}{l} x_{i} \\ y_{i} \end{array}\right]=\left[\begin{array}{l} \Delta x_{i} \\ \Delta y_{i} \end{array}\right]+\left[\begin{array}{l} x^{0} \\ y^{0} \end{array}\right]

$x^{i} = Δ x^{i} x^{0} + x^{o} = [x_{i} y_{i}] = [Δ x_{i} Δ y_{i}] + [x^{0} y^{0}]$

其中

\Delta \boldsymbol{x}^{i} \boldsymbol{x}^{0}

$Δ x^{i} x^{0}$

表示

\boldsymbol{x}^{0}

$x^{0}$

到

\boldsymbol{x}^{i}

$x^{i}$

的坐标偏移。现在我们设置形变子区中与之前

\boldsymbol{x}^{i}

$x^{i}$

相对应的当前坐标点为

′

[

′

]

\boldsymbol{x}^{i’} =\left[\begin{array}{ll}x_{i}’ & y_{i}’\end{array}\right]^{T}

$x^{i^{'}} = [x_{i}^{'} y_{i}^{'}]^{T}$

，与之前中心点

\boldsymbol{x}^{0}

$x^{0}$

相对应的形变子区中心点为

\boldsymbol{x}^{d}

$x^{d}$

。与上式同理，我们同样可以得到

′

\boldsymbol{x}^{i’}

$x^{i^{'}}$

的表达式为

′

[

′

]

[

′

]

[

]

\boldsymbol{x}^{i’}=\Delta \boldsymbol{x}^{i’} \boldsymbol{x}^{0}+\boldsymbol{x}^{o}=\left[\begin{array}{l} x_{i}’ \\ y_{i}’ \end{array}\right]=\left[\begin{array}{l} \Delta x_{i}’ \\ \Delta y_{i}’ \end{array}\right]+\left[\begin{array}{l} x^{0} \\ y^{0} \end{array}\right]

$x^{i^{'}} = Δ x^{i^{'}} x^{0} + x^{o} = [x_{i}^{'} y_{i}^{'}] = [Δ x_{i}^{'} Δ y_{i}^{'}] + [x^{0} y^{0}]$

其中

′

\Delta \boldsymbol{x}^{i’} \boldsymbol{x}^{0}

$Δ x^{i^{'}} x^{0}$

表示

\boldsymbol{x}^{0}

$x^{0}$

到

′

\boldsymbol{x}^{i’}

$x^{i^{'}}$

的坐标偏移。注意，没有使用形变子区中心点作为参考点，是有两个原因的，

第一个原因是由于本身

\boldsymbol{x}^{d}

$x^{d}$

对于我们来说依然是未知点，它只不过是一个

′

\boldsymbol{x}^{i’}

$x^{i^{'}}$

特例罢了，这里需要用一个已知点作为参考

，

还有一个原因会在形函数推导那一部分提到，这里先不引入。

在这个式子当中，最重要的就是计算这里的

′

\Delta \boldsymbol{x}^{i’} \boldsymbol{x}^{0}

$Δ x^{i^{'}} x^{0}$

，因为在获得这个值后就找到形变后与之前子区一一对应的像素点坐标，从而可以计算整个子区图像的位移场，最后即可计算该区域的形变或者受力了。而这个未知量的求解，需要引入一个有限元分析中的概念——

形函数（Shape Function）

。对于一个区域或者一个单元，其形变是可以通过数学模型来进行表示的，而这个用于描述的数学模型就是形函数（图像处理中常见的仿射变换实质就是一个形函数）。形函数的阶数越高，则可以描述的形变就越复杂。因此对于

′

\Delta \boldsymbol{x}^{i’} \boldsymbol{x}^{0}

$Δ x^{i^{'}} x^{0}$

是可以用形函数来表达的，这里设形函数关系为

W

$W$

，

形函数参数

（Shape Function Parameters, SFPs）为

P

$P$

，我们有

′

(

)

\Delta \boldsymbol{x}^{i’} \boldsymbol{x}^{0}=W(\Delta \boldsymbol{x}^{i} \boldsymbol{x}^{0},P)

$Δ x^{i^{'}} x^{0} = W (Δ x^{i} x^{0}, P)$

那么现在关系式就全部建立完成了，接下来，

如何建立这个形函数以及如何知道最合适的形函数参数

成为了下一步的目标，首先是形函数的建立，这需要根据实际情况选择合适阶数的形函数关系，留到下一章进行探讨。那么如何知道最合适的形函数参数呢？这就需要用到数字图像相关最核心的内容——相关运算。

在信号与系统中，评判两个信号的相似程度就是对他们进行相关运算

，二维图像实质也是一种信号，因此评判参考子区和形变子区是否相似也是可以用相关运算的。

这样的话我们就可以将两者相关运算作为一个目标函数（其结果为

相关标准

，用于衡量两者的相似性， Correlation Criterion），通过建立好的形函数关系式以及一组形函数参数初值

P_{0}

$P_{0}$

，通过对相关标准的梯度下降法迭代求解，即可以找到一组最合适的形函数参数最优解

∗

P^{*}

$P^{*}$

，此时所得到的形变子区就是与真实的形变情况最为接近的，从而实现了参考子区与形变子区之间的匹配！

二维数字图像本身是对于光强的一种采样，即本身是离散点，考虑到匹配的精度，需要对形变图像进行插值，以实现亚像素级别的匹配。经过插值运算后，参考子区和形变子区都可以写成函数的形式，即

(

)

f_{i}=F\left(\boldsymbol x^{o}+\Delta \boldsymbol{x}^{i} \boldsymbol{x}^{0}\right)

$f_{i} = F (x^{o} + Δ x^{i} x^{0})$

(

)

g_{i}=G\left(\boldsymbol x^{o}+\boldsymbol{W}\left(\Delta \boldsymbol{x}^{i} \boldsymbol{x}^{0}, \boldsymbol{P}\right)\right)

$g_{i} = G (x^{o} + W (Δ x^{i} x^{0}, P))$

将上面的推导进行归纳，整个运算的实质就是

通过给定一组形函数参数初值

0

P_{0}

$P_{0}$

，对目标函数（相关标准）不断迭代优化从而得到一组最优解

∗

P^{*}

$P^{*}$

。

2.形函数

在二维数字图像相关中，最常采用的形函数有0阶形函数（

W^{SF0}

$W^{S F 0}$

）、1阶形函数（

W^{SF1}

$W^{S F 1}$

）和2阶形函数（

W^{SF2}

$W^{S F 2}$

）。阶数越高，能描述的形变就越复杂，但待求解的的位置量也会越多。如图所示的就是这三种形函数的示意图
¹

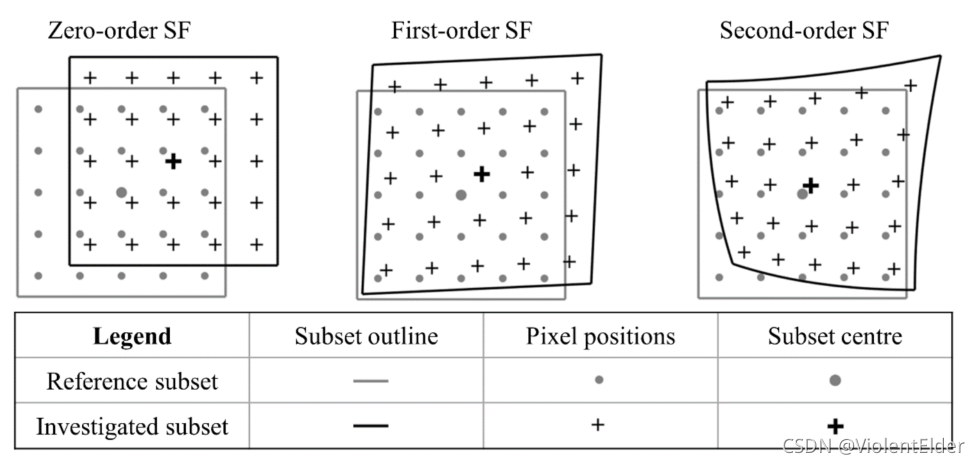
在这里插入图片描述

0阶形函数

：只能描述位移变化，无法描述拉伸或者扭曲（速度较快，适合用于小形变系统的实时检测）

(

)

[

]

[

]

\boldsymbol{W}^{S F 0}\left(\Delta \boldsymbol{x}^{i} \boldsymbol{x}^{0}, \boldsymbol{P}^{S F 0}\right)=\left[\begin{array}{ccc} 1 & 0 & u \\ 0 & 1 & v \end{array}\right]\left[\begin{array}{c} \Delta x_{i} \\ \Delta y_{i} \\ 1 \end{array}\right]

$W^{S F 0} (Δ x^{i} x^{0}, P^{S F 0}) = [1001 u v] ⎣ ⎡ Δ x_{i} Δ y_{i} 1 ⎦ ⎤$

1阶形函数

：能描述子区位移和拉伸（仿射变换），但不能描述扭曲（适合用于小形变系统）

(

)

[

]

[

]

\boldsymbol{W}^{S F 1}\left(\Delta \boldsymbol{x}^{i} \boldsymbol{x}^{0}, \boldsymbol{P}^{S F 1}\right)=\left[\begin{array}{ccc} 1+u_{x} & u_{y} & u \\ v_{x} & 1+v_{y} & v \end{array}\right]\left[\begin{array}{c} \Delta x_{i} \\ \Delta y_{i} \\ 1 \end{array}\right]

$W^{S F 1} (Δ x^{i} x^{0}, P^{S F 1}) = [1 + u_{x} v_{x} u_{y} 1 + v_{y} u v] ⎣ ⎡ Δ x_{i} Δ y_{i} 1 ⎦ ⎤$

2阶形函数

：能描述子区位移、拉伸和扭曲（适合用于大形变系统）

(

)

[

]

[

]

\boldsymbol{W}^{S F 2}\left(\Delta \boldsymbol{x}^{i} \boldsymbol{x}^{0}, \boldsymbol{P}^{S F 2}\right)=\left[\begin{array}{cccccc} \frac{1}{2} u_{x x} & u_{x y} & \frac{1}{2} u_{y y} & 1+u_{x} & u_{y} & u \\ \frac{1}{2} v_{x x} & v_{x y} & \frac{1}{2} v_{y y} & v_{x} & 1+v_{y} & v \end{array}\right]\left[\begin{array}{c} \Delta x_{i}^{2} \\ \Delta x_{i} \Delta y_{i} \\ \Delta y_{i}^{2} \\ \Delta x_{i} \\ \Delta y_{i} \\ 1 \end{array}\right]

$W^{S F 2} (Δ x^{i} x^{0}, P^{S F 2}) = [\frac{1}{2} u_{x x} \frac{1}{2} v_{x x} u_{x y} v_{x y} \frac{1}{2} u_{y y} \frac{1}{2} v_{y y} 1 + u_{x} v_{x} u_{y} 1 + v_{y} u v] ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ Δ x_{i}^{2} Δ x_{i} Δ y_{i} Δ y_{i}^{2} Δ x_{i} Δ y_{i} 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

由上述式子我们可以得到不同阶数形函数需要求解的参数为：

[

]

\boldsymbol{P}^{S F 0}=\left[\begin{array}{llllllllllll} u & v\end{array}\right]^{T}

$P^{S F 0} = [u v]^{T}$

[

]

\boldsymbol{P}^{S F 1}=\left[\begin{array}{llllllllllll} u & u_{x} & u_{y} & v & v_{x} & v_{y} \end{array}\right]^{T}

$P^{S F 1} = [u u_{x} u_{y} v v_{x} v_{y}]^{T}$

[

]

\boldsymbol{P}^{S F 2}=\left[\begin{array}{llllllllllll} u & u_{x} & u_{y} & u_{x x} & u_{x y} & u_{y y} & v & v_{x} & v_{y} & v_{x x} & v_{x y} & v_{y y} \end{array}\right]^{T}

$P^{S F 2} = [u u_{x} u_{y} u_{x x} u_{x y} u_{y y} v v_{x} v_{y} v_{x x} v_{x y} v_{y y}]^{T}$

那这里的每一项参数代表什么呢？从上一节的内容，我们可以知道，对于参考子区中任意一个像素点，其对应的形变子区上的映射点坐标都可以写成

参考子区对应点的坐标值+

/

Y

X/Y

$X / Y$

方向的偏移量

的形式。同时，由于两个点本身相关，因此这个偏移量和参考子区对应点坐标是有关系的。因此，我们可以得到以下关系式，设参考子区上的某一点

(

)

f(x,y)

$f (x, y)$

，设其在形变子区上的映射点为

(

)

g(\widetilde{x},\widetilde{y})

$g (x, y)$

，我们有：

(

)

\widetilde{x}=x+u(x,y)

$x = x + u (x, y)$

(

)

\widetilde{y}=y+v(x,y)

$y = y + v (x, y)$

对两式进行二阶泰勒展开
⁵
，我们可以获得

\tilde{x}= x_{0}+u+u_{x} \Delta x+u_{y} \Delta y+\frac{1}{2} u_{x x} \Delta x^{2} +\frac{1}{2} u_{y y} \Delta y^{2}+u_{x y} \Delta x \Delta y

$\tilde{x} = x_{0} + u + u_{x} Δ x + u_{y} Δ y + \frac{1}{2} u_{x x} Δ x^{2} + \frac{1}{2} u_{y y} Δ y^{2} + u_{x y} Δ x Δ y$

\tilde{y}= y_{0}+v+U_{x} \Delta x+v_{y} \Delta y+\frac{1}{2} v_{x x} \Delta x^{2} +\frac{1}{2} v_{y y} \Delta y^{2}+v_{x y} \Delta x \Delta y

$\tilde{y} = y_{0} + v + U_{x} Δ x + v_{y} Δ y + \frac{1}{2} v_{x x} Δ x^{2} + \frac{1}{2} v_{y y} Δ y^{2} + v_{x y} Δ x Δ y$

而

形函数的参数就是展开式中各项的系数

，值得注意的是，展开式中的常数项

)

(x_{0},y_{0})

$(x_{0}, y_{0})$

，考虑到每一个子区只会计算一个形函数，因此单一子区内各点的计算均要使用相同的常数项，这也正是上一节中

每个点均以参考子区中心点坐标作为参考

的原因了。

在实际进行相关运算的过程中，需要根据实际情况选择合适的形函数，形函数选择的越好则计算得到的形变子区越接近真实情况，计算的值也会更加准确！

3.相关标准

相关标准在相关运算中相当于最后的评价函数，选择合适的相关标准对于迭代优化的速度有很大作用。一个评价函数的好坏我个人认为是要满足

快收敛

、

足够“凸”

、

“抗噪声”

，快收敛使得整体优化能尽快逼近最优解。足够“凸”使得每次迭代优化步进都会很大，同时最优解点确实够好。而抗噪声则确保了所逼近的最优解点和实际情况相符，而不是由于噪声导致的异常值，减小误差。这一块我自己还不太能吃透，就直接搬结果吧。

在Bing Pan等人的文章Equivalence of digital image correlation criteria for pattern matching
⁶
中介绍了各种相关标准的算术推导以及相互之间的转换，其中最好的三种相关标准为

零均值归一化互相关标准（Zero-Normalized Cross-Correlation Criterion, ZNCC）、零均值归一化最小距离平方标准（Zero-Normalized Sum of Squared Differences Criterion, ZNSSD）和最优化参数的距离平方标准（Parametric Sum of Squared Difference, PSSDab）

。
⁷

在这里插入图片描述

这三种标准相互之间可以互相转换，在对最终结果的推导上是一致的。Bing Pan等人还在文章中测试分别使用PSSD与ZNSSD作为相关标准时候的计算效率，PSSD会更好一些。当然选用哪种标准还是要看实际情况来选择。

其他知识

考虑篇幅

~~（我太懒了而且没搞太懂）~~

，相关运算的其他知识点我就在这里提一嘴，之后有空再单独写帖子补充吧。

由于需要对形变图像进行精确插值，目前

最常采用的插值运算为双三次b样条插值（bicubic b-spline interpolation）
上述的三种相关标准，对于高频噪声都比较敏感，因此

需要对参考图像和形变图像都进行高斯滤波，滤除高频噪声

（具体的参数需要研究，由于低通滤波器会将很多纹理模糊）
基于相关标准来优化形函数参数实质是个非线性优化问题，目前最常采用的计算方式为

逆合成高斯-牛顿法——IC-GN算法（Inverse compositional Gauss-Newton method）

，推荐阅读

数字图像相关（Digital Image Correlation, DIC）中的非线性优化方法（FA-GN与IC-GN）
优化的

开始需要提供一组形函数参数初值

，这组初值越接近最优解，迭代速度提升也就越快，同时其合理性也决定了所得最优解与真实值之间的误差

（因为优化等于一个寻找峰顶的过程，我们想要的是最高的峰顶，但如果初值位置不位于最高峰，则找到的峰顶并不是最理想的）。

三.ADIC2D代码解释

在github上下载好源码，根据readme下载好需要的数据集，我们即可完成对于ADIC2D项目的部署，注：我是在Matlab 2018a上进行的调试。如图，是部署好后的各文件含义

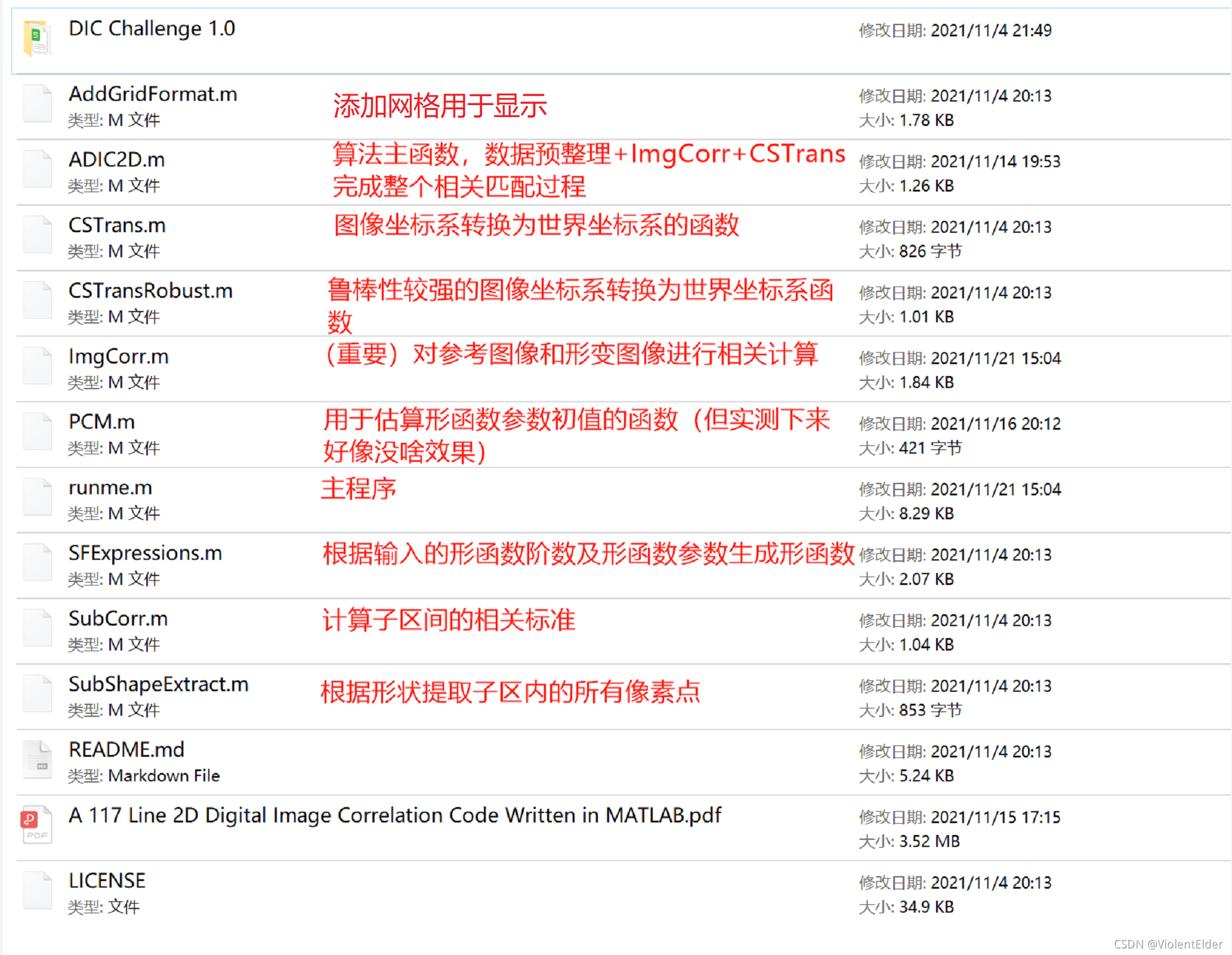
在这里插入图片描述

整个项目的调用关系及框架如图所示

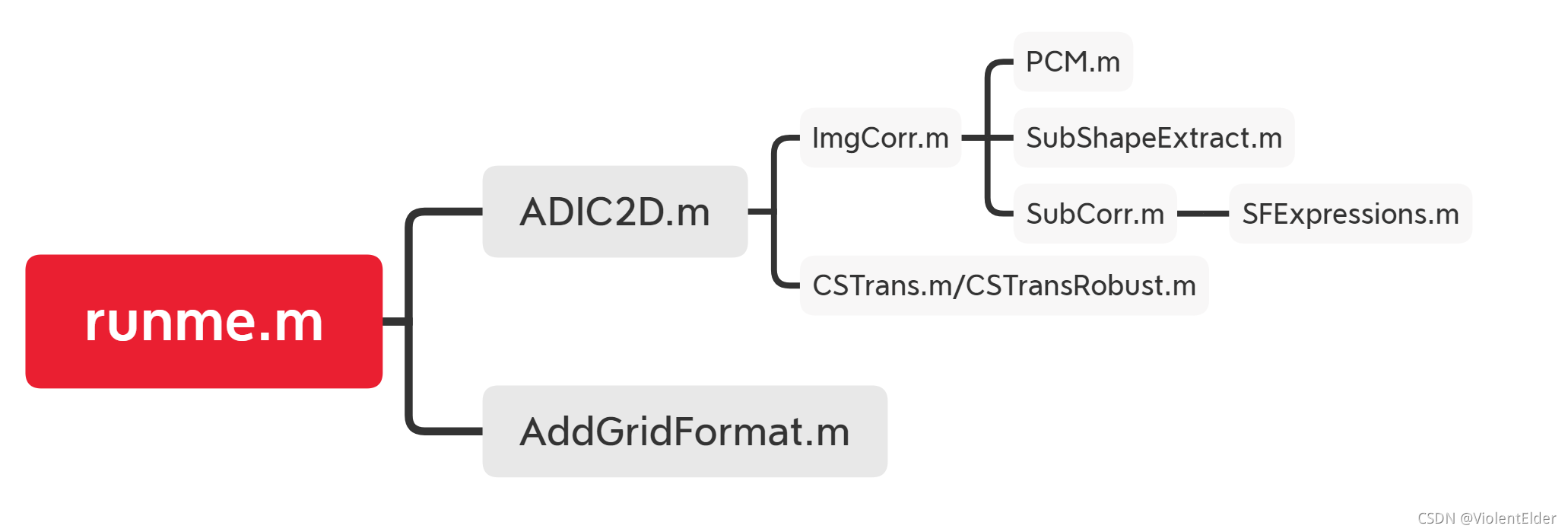
部署完成之后直接运行
runme.m
文件即可，数据集的选择、ADIC2D算法输入参数均可在文件开头进行修改。具体可修改参数如下：

% runme.m参数输入部分解释
Sample=3; % EN:which sample to analyse CH:选择使用的数据集序号1——3
FileNames=ImageNamesLoad(Sample); % load appropriate images for chosen sample
Mask=ones(size(im2double(imread(FileNames{1})))); % EN:define a mask that includes all pixels of the image CH:设定一个蒙版决定使用图片中的那些区域，即ROI

% Function inputs (which set up the DIC analysis)
GaussFilter=[0.4,5];% 高斯滤波参数[sigma, kernal size]，用于滤除高频噪声
StepSize=5;         % 子区步进
SubSize=41;         % 子区大小
SubShape='Circle';  % 子区形状
SFOrder=1;          % 形函数阶数（0,1,2）
RefStrat=0;         % 子区开始编号
StopCritVal=1e-4;   % 停止迭代的标准
WorldCTs=0;         % 世界坐标系下的标定点位置
ImageCTs=0;         % 图像坐标系下的标定点位置
rho=0;              % 标定板厚度（mm）

之后
runme.m
会调用
ADIC2D
算法函数将读入的数据集进行处理，之后会输出处理好的数据集结构体。
runme.m
的后半部分是利用输出的数据结果进行显示和计算误差，包括某副图像子区沿

X/Y

$X / Y$

方向的位移情况、位移结果的均方根误差等。这部分代码都比较易读，直接说一下
ADIC2D
及其子函数的算法逻辑吧

在这里插入图片描述

1.ImgCorr

ImgCorr
函数就是按照上一个大章节中的思路来书写的，下面是它的算法概要

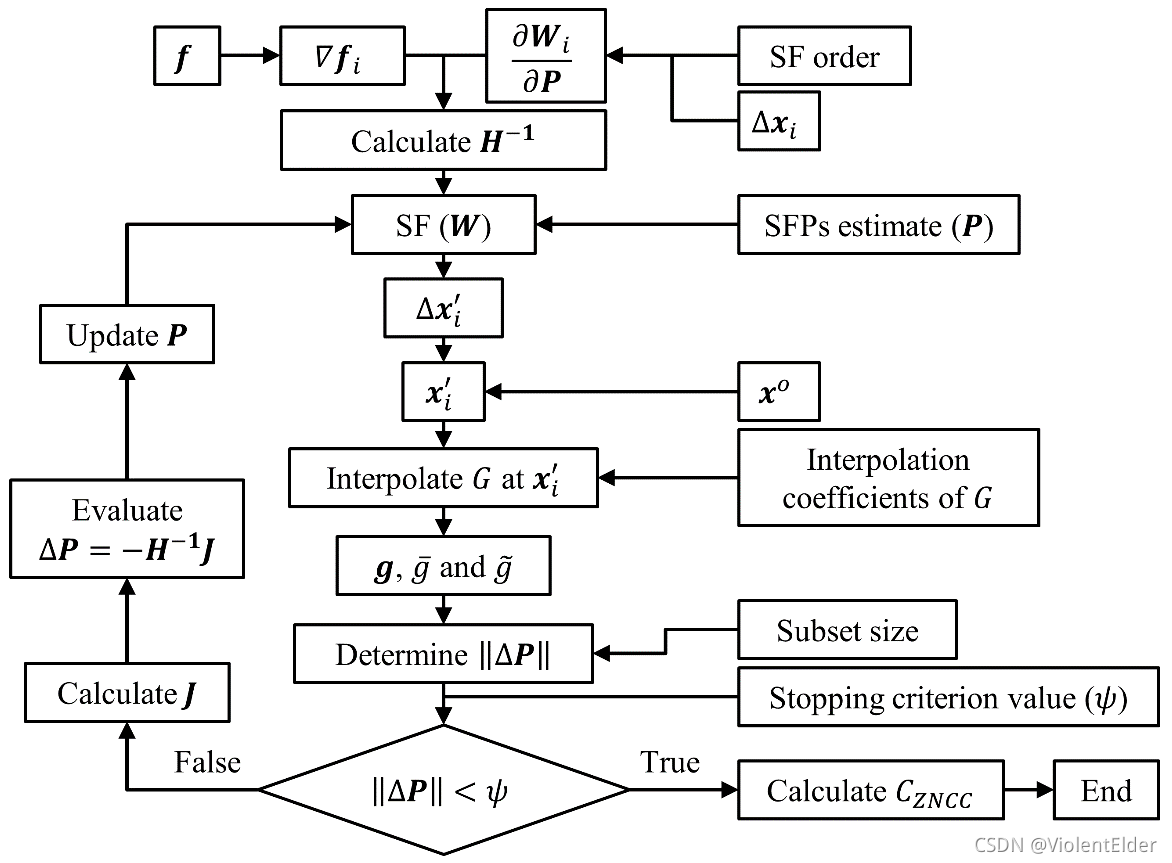
在这里插入图片描述

2.SubCorr

SubCorr
函数是利用IC-GN的方法来优化形函数参数，直到得到最优解，从而输出最佳匹配的形变子区信息，具体代码逻辑请参照论文
¹
及其源码，这里仅展示其算法框架图

在这里插入图片描述

四.写在最后

这是我在自己做课题过程中读到的一篇写的很通透的论文，数字图像相关其实是很成熟的技术了，但是就目前看来在国内，这一块的研究还很少，即使是有相关的应用也大都是照搬理论，并没有对于这种技术详细的描述和深入的解释。本人也是个小白，希望能通过这篇帖子将这种技术说的稍微清楚些，其中如果有任何理解上的偏差和错误还望业界的大佬能多多指正，确保输出的知识足够准确和客观。之后我把自己的课题理清楚后，应该会写一个小的demo作为分享，方便相关学者们能更快的理解和使用这种技术。最后非常感谢Atkinson D, Becker T对于这份知识的分享。

推荐个应用该技术的网站，方便大家进一步深入

http://www.ncorr.com/index.php/dic-algorithms

参考引用

Atkinson D, Becker T. A 117 Line 2D Digital Image Correlation Code Written in MATLAB[J]. Remote Sensing, 2020, 12(18): 2906.

↩︎

↩︎

↩︎

↩︎

↩︎
Chu T C, Ranson W F, Sutton M A. Applications of digital-image-correlation techniques to experimental mechanics[J]. Experimental mechanics, 1985, 25(3): 232-244.

↩︎
周轶昊. 基于双目视觉的物体表面三维复杂运动重建及其应用[D].复旦大学,2012.

↩︎
Khoo S W, Karuppanan S, Tan C S. A review of surface deformation and strain measurement using two-dimensional digital image correlation[J]. Metrology and Measurement Systems, 2016, 23(3).

↩︎
Lu H, Cary P D. Deformation measurements by digital image correlation: implementation of a second-order displacement gradient[J]. Experimental mechanics, 2000, 40(4): 393-400.

↩︎
Pan B, Xie H, Wang Z. Equivalence of digital image correlation criteria for pattern matching[J]. Applied optics, 2010, 49(28): 5501-5509.

↩︎
Sutton M A, Orteu J J, Schreier H. Image correlation for shape, motion and deformation measurements: basic concepts, theory and applications[M]. Springer Science & Business Media, 2009.

↩︎

原文链接：https://blog.csdn.net/weixin_43560489/article/details/121322597

目录

前言