目录
1.算法仿真效果
matlab2022a仿真结果如下:
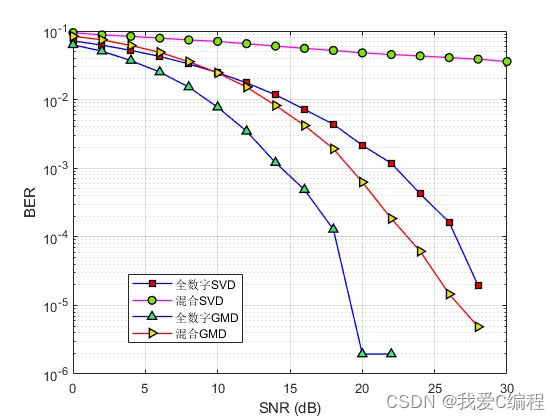
2.算法涉及理论知识概要
毫米波通信作为第五代移动通信(5G)和未来通信系统的重要技术,能够提供更高的数据传输速率和更大的系统容量。然而,毫米波通信在传输过程中容易受到路径损耗和大气衰减的影响,因此需要采用有效的波束形成算法来提高信号质量。混合波束形成技术结合了射频(RF)和基带(BB)波束形成的优点,能够有效地抵消信道损耗。
混合GMD(Generalized Matching Pursuit)波束形成算法是一种用于毫米波大规模MIMO系统的波束形成技术。其基本思想是通过在RF和BB域分别进行波束形成,来提高信号的传输效率和可靠性。考虑一个具有$N_t$个发射天线和$N_r$个接收天线的毫米波大规模MIMO系统。接收信号可以表示为:

其中,$\mathbf{y}$是接收到的信号向量,$\mathbf{H}$是信道矩阵,$\mathbf{x}$是发送的信号向量,$\mathbf{n}$是噪声向量。
混合GMD波束形成算法的目标是选择适当的RF和BB权重向量$\mathbf{w}_r$和$\mathbf{w}_b$,使得接收信号的信噪比(SNR)最大化。接收信号为:

波束形成的目标可以表示为:

实现过程
-
信道估计
:在实际系统中,信道信息通常是未知的,因此需要进行信道估计。可以通过发送已知的训练序列,并通过接收到的信号估计RF和BB信道矩阵。 -
RF权重计算
:利用估计得到的RF信道矩阵,计算RF权重向量$\mathbf{w}_r$。可以采用GMD算法选择与信道向量$\mathbf{h}_r$成正比的权重向量。 -
BB权重计算
:利用估计得到的BB信道矩阵,计算BB权重向量$\mathbf{w}_b$。同样,可以采用GMD算法选择与信道向量$\mathbf{h}_b$成正比的权重向量。 -
信号传输
:将发送的信号$\mathbf{x}$通过RF和BB权重向量进行波束形成,得到最终的传输信号$\hat{x}$。
3.MATLAB核心程序
........................................................................
%合并
GH = G';UH=U';
G_1 = GH(1:Nsym,:);
yc_svd = UH(1:Nsym,:)*yo_svd;
yc_gmd = G_1*yo_gmd;
W_hysvd = Wbb(:,:,jc)'*W_somp';
yc_somp_svd = sqrt(Nsym/Nrf)*W_hysvd*yo_hysvd;
W_hygmd = G_SOMP'*W_somp';
yc_somp_gmd = sqrt(Nsym/Nrf)*W_hygmd*yo_hygmd;
%SVD解码
tmp1 = func_VBLAST_decoder(yc_svd,Nsym,S(:,1:Nsym));
msg_svd = func_deQAM16(tmp1);
tmp2 = func_VBLAST_decoder(yc_somp_svd,Nsym,S(:,1:Nsym));
msg_hysvd = func_deQAM16(tmp2);
%GMD-SIC解码
tmp3 = func_VBLAST_decoder(yc_gmd,Nsym,M(:,1:Nsym));
msg_gmd = func_deQAM16(tmp3);
tmp4 = func_VBLAST_decoder(yc_somp_gmd,Nsym,M2);
msg_hygmd = func_deQAM16(tmp4);
%错误计数
cnt_svd = cnt_svd + sum(msg1~= msg_svd);
cnt_hygmd = cnt_hygmd + sum(msg1~= msg_hysvd);
cnt_gmd = cnt_gmd + sum(msg1~= msg_gmd);
cnt_hysvd = cnt_hysvd + sum(msg1~= msg_hygmd);
end
end
err_svd(ij) = cnt_svd/N_tbits;
err_gmd(ij) = cnt_gmd/N_tbits;
err_hysvd(ij) = cnt_hysvd/N_tbits;
err_hygmd(ij) = cnt_hygmd/N_tbits;
end
figure;
semilogy(SNRss,smooth(err_svd),'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
semilogy(SNRss,smooth( err_hygmd),'-mo',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.5,0.9,0.0]);
hold on
semilogy(SNRss,smooth(err_gmd),'-b^',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.2,0.9,0.5]);
hold on
semilogy(SNRss,smooth( err_hysvd),'-r>',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
hold on
xlabel('SNR (dB)')
ylabel('BER')
legend('全数字SVD','混合SVD','全数字GMD','混合GMD');
grid on
0X_022m
4.完整算法代码文件
V