1.常见运算
转置(transpose)
是矩阵的重要操作之一。矩阵的转置是以对角线为轴的镜像,这条从左上角到右下角的对角线被称为主对角线(main diagonal)。
我们将矩阵 A 的转置表示为 A ⊤ ,定义如下
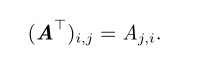
向量可以看作是只有一列的矩阵。对应地,向量的转置可以看作是只有一行的矩阵。
标量可以看作是只有一个元素的矩阵。因此,标量的转置等于它本身,
a
=
a
⊤ 。
矩阵相加
矩阵的形状一样。
两个矩阵相加是指对应位置的元素相加,比如
C
=
A
+
B
,其中 C i,j = A i,j + B i,j 。
标量和矩阵相乘
需将其与矩阵的每个元素相乘
比如
D
= a ·
B
+ c,其中 D i,j = a · B i,j + c
矩阵和向量相加
向量 b 和矩阵A 的每一行相加
C
=
A
+
b
,其中 C i,j = A i,j + b j
这种隐式地复制向量 b 到很多位置的方式,被称为广播(broadcasting)
矩阵乘法
两个矩阵 A 和 B 的矩阵乘积
(matrix product)是第三个矩阵 C。为了使乘法定义良好,矩阵 A 的列数必须和矩
阵 B 的行数相等。
如果矩阵 A 的形状是 m×n,矩阵 B 的形状是 n×p,那么矩阵C 的形状是 m×p。
我们可以通过将两个或多个矩阵并列放置以书写矩阵乘法,例如
C
=
AB
具体地,该乘法操作定义为
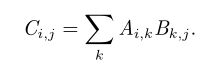
元素对应
乘积
(element-wise product)或
者Hadamard 乘积(Hadamard product)
两个矩阵中对应元素的乘积
记为
A
⊙
B
![]()
矩阵
![]()
与
![]()
矩阵
![]()
的Hadamard积记为
![]()
。其元素定义为两个矩阵对应元素的乘积
![]()
的m×n矩阵 。
两个相同维数的向量 x 和 y 的点积(dot product)可看作是矩阵乘积
x
⊤
y
2.基本性质
分配律
A
(
B
+
C
) =
AB
+
AC
结合律
A
(
BC
) = (
AB
)
C
矩阵乘积并不满足交换律(AB = BA 的情况并非总是满足)
两个向量的点积(dot product)满足交换律
x
⊤
y
=
y
⊤
x
矩阵乘积的转置
(
AB
) ⊤ =
B
⊤
A
⊤
线性方程组
Ax
=
b
其中 A ∈ R m×n 是一个已知矩阵,b ∈ R m 是一个已知向量,x ∈ R n 是一个我们要
求解的未知向量。
向量 x 的每一个元素 x i 都是未知的。矩阵
A
的每一行和
b
中对
应的元素构成一个约束。
A 1,: x = b 1
A 2,: x = b 2
···
A m,: x = b m
也可以写成
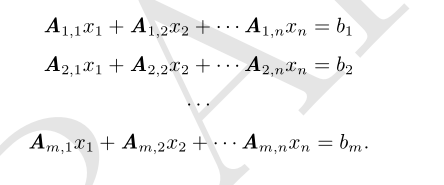
转载于:https://www.cnblogs.com/bigcome/p/9989232.html