博客

最近在学群体优化算法，做个学习笔记吧，本人蒟蒻，有不对的地方还情多多包涵。

1.粒子群算法的理解。

粒子群算法是一种智能优化算法，模拟的是鸟内捕食行为。假设有一群鸟，在一个区域内觅食，这个区域内只有一个食物（最优解），但是每个鸟只知道自己距食物的距离，还有靠食物最近的鸟的距离（群体最优解），这样，他们的觅食行为就收到三个方面的约束。

（1）距离食物最近的鸟的位置，这样所有的其他鸟都会向这只鸟靠拢，即所有点都会向当前全局最优解学习，靠拢。

（2）光有全局最优解，最后得到的解最优也只能是初始状态的最优解，因此，每个鸟在靠近全局最优解的过程中也会计算自己与食物之间的距离，有可能在某一时刻，自己的距离比全局最优解还近，那么更新全局最优解，同时变更群体的学习方向。这就是个体最优解。

（3）自身惯性。这是粒子继承先前速度的能力。一个较大的惯性有助于全局搜索，而一个较小的惯性有助于局部搜索。因此，在平常设计中，我们将惯性w设置为动态惯性，确保前期全局搜索能力强，但在后期局部搜索能力强，从而提高算法精度。

所以，假设在一个D维的搜索空间中，由n个粒子组成的种群X=（X1,X2….Xn），其中第i个粒子向量表示为Xi=

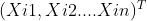
,表示粒子在D维搜索空间的位置，第i个粒子的速度为Vi=

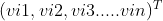
,个体极值为Pi=

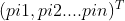
,种群极值为Pg=

;

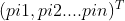
则速度更新公式为

其中，w为惯性权重，k为迭代次数，Vid为粒子的速度；c1和c2为非负常数，也叫作加速度因子；r1和r2为【0,1】的分布随机数。

2.粒子群算法的求解过程。

这里我们以01背包问题为例来模拟粒子群算法。01背包问题是著名的非线性寻优问题，适应度由价格和体积决定，而质量是总约束条件。整个算法流程看代码吧，很清晰易懂的。

clear;
clc;
close all;

a=[95,4,60,32,23,72,80,62,65,46];        %物品体积
c=[55,10,47,5,4,50,8,61,85,87];          %物品价值
b=269;                                    %背包重量

%初始化种群
Dim=10;           %维度
xSize=20;         %种群数
maxgen=30;        %迭代次数
c1=0.7;
c2=0.7;           %加速因子
w=0.8;            %定义惯性因子
%
A=repmat(a,xSize,1);      %将a扩展成30*10的矩阵
C=repmat(c,xSize,1);      %c扩展为30*10的矩阵
x=round(rand(xSize,Dim)); %随机一个30*10的矩阵
v=rand(xSize,Dim)         %随机一个30*10的速度矩阵
xbest=zeros(xSize,Dim);   %单个粒子的初始最佳位置
fxbest=zeros(xSize,1);    %xbext的适应度
gbest=zeros(1,Dim);       %全局最优解
fgbest=0;                 %全局最优解的适应度
%
%寻找粒子群最优位置和单个粒子
iter=0;
while iter<maxgen
    iter=iter+1;
    fx=sum((C.*x)');         %粒子适应度，即背包内物品的价格
    sx=sum((A.*x)');         %限制函数，背包内物品的体积
    for i=1:xSize
        if sx(i)>269
            fx(i)=0;         %超过体积，适应度为0
        end
    end
    for i=1:xSize
        if fxbest(i)<fx(i)   %当粒子适应度大于最佳适应度时，替代
            fxbest(i)=fx(i);
            xbest(i,:)=x(i,:);
        end
    end
    if fgbest<max(fxbest)
        [fgbest,g]=max(fxbest);
        gbest=xbest(g,:)     %当存在粒子的最佳适应度fxbext(i)大于种群最佳适应度fgbext(i)时，替代
    end
    for i=1:xSize
        if x(i,:)==gbest
            x(i,:)=round(rand(1,Dim));     %当某个粒子的位置为最佳位置时，重新赋值，以防止陷入局部最优解
        end
    end
    R1=rand(xSize,Dim);
    R2=rand(xSize,Dim);
    v=v*w+c1*R1.*(xbest-x)+c2*R2.*(repmat(gbest,xSize,1)-x);%速度迭代公式产生新的速度
    x=x+v;          
    for i=1:xSize   %更新粒子群的位置
        for j=1:Dim
            if x(i,j)<0.5
                x(i,j)=0;
            else x(i,j)=1;   %粒子的位置只有（0,1）两种状态
            end
        end
    end
end

fgbest
sgbest=sum((a.*gbest)')
disp(gbest);

最后的结果中，gbest的结果，0代表没选，1代表选。