A*算法说明
文章目录
前言
因为最近要写一个毕业设计,有用到自动寻路的功能,因为我要在一个机器里跑算法然后控制机器人自动按照路线到达目的地,所以用Python等解释型语言或Unity等游戏引擎写这个算法都不太合适,我使用的机器要尽可能不在里面安装大型的库。所以我就用C++实现了一个A*算法。因为实现了之后觉得这个算法比较有意思,就又写了一个GUI程序,可以选择显示过程,即以可视化查看算法寻路的过程。
我写的A*算法在能找到最优路线的前提下,支持斜方位移动
(可以选择是否允许斜方位移动)
,支持设置道路拥堵情况
(默认所有位置路况为1,如果设置大于1,则表示拥堵,数值越大则越拥堵,如果设置小于1,则表示比默认路况更为畅通,数值越小则越通畅,如果设置为0表示异常畅通,即通过此道路代价为0,如果设置为负数表示
+
∞
+\infty
+
∞
,即无法通行)
,支持选择是否使用优先队列,支持读取和保存地图,在GUI程序里支持显示寻找路线的动画。
原理说明
A*可以认为是添加了启发式函数的Dijkstra算法,在Dijkstra算法的基础上,构造一个函数
h
(
n
)
h(n)
h
(
n
)
,n为当前扩展结点,
h
(
n
)
h(n)
h
(
n
)
返回结点n到终点的开销估计。然后建立函数
f
(
n
)
=
g
(
n
)
+
h
(
n
)
f(n)=g(n)+h(n)
f
(
n
)
=
g
(
n
)
+
h
(
n
)
,其中
g
(
n
)
g(n)
g
(
n
)
为从起点到结点n已经使用了的代价,所以
f
(
n
)
f(n)
f
(
n
)
可以理解为是
“从起点出发经过结点n再到终点的代价估计”
。
关于
h
(
n
)
h(n)
h
(
n
)
的构造返回值的问题会对A*算法造成影响:
如果构造
h(
n
)
≡
0
h(n) \equiv 0
h
(
n
)
≡
0
,那么该A*算法就已经退化为了Dijkstra算法,一定能解得最优解但是运行效率最低。
如果构造
h(
n
)
≡
h
∗
(
n
)
h(n) \equiv h^*(n)
h
(
n
)
≡
h
∗
(
n
)
,则该A*算法不仅能够保证一定能解得最优解,而且运行效率在所有能保证解得最优解的A*算法中是最高的。其中
h∗
(
n
)
h^*(n)
h
∗
(
n
)
表示结点n到终点的实际代价。
如果构造的
h(
n
)
h(n)
h
(
n
)
对所有的n有
h(
n
)
≤
h
∗
(
n
)
h(n) \leq h^*(n)
h
(
n
)
≤
h
∗
(
n
)
,则该A*算法能保证一定能得到最优解,但是效率略低于上述
h(
n
)
≡
h
∗
(
n
)
h(n) \equiv h^*(n)
h
(
n
)
≡
h
∗
(
n
)
的情况。
如果构造的
h(
n
)
h(n)
h
(
n
)
存在n使得
h(
n
)
>
h
∗
(
n
)
h(n)>h^*(n)
h
(
n
)
>
h
∗
(
n
)
,则该A*算法不一定能得到最优解(当然运气好的时候也有可能会解得最优解,但是不能保证)。
所以,我们应该构造满足对所有的n有
h
(
n
)
≤
h
∗
(
n
)
h(n) \leq h^*(n)
h
(
n
)
≤
h
∗
(
n
)
的
h
(
n
)
h(n)
h
(
n
)
。虽然
h
(
n
)
≡
h
∗
(
n
)
h(n) \equiv h^*(n)
h
(
n
)
≡
h
∗
(
n
)
效果最好,但是面对复杂的地图,这种启发式函数可欲而不可求
(当然,
h
(
n
)
h(n)
h
(
n
)
函数必须要是复杂度极低的,不能说我为了估计结点n到终点的代价而真的去用A*算法本身以n为起点跑一遍然后得到实际最小代价,这样就没有意义了,引进
h
(
n
)
h(n)
h
(
n
)
就是为了“剪支”的,如果在
h
(
n
)
h(n)
h
(
n
)
里对n展开用A*计算,那剪支的意义何在?都已经展开了)
。
构造好
f
(
n
)
f(n)
f
(
n
)
后,构造一个优先队列(如果对效率要求不高,直接用普通的队列也可以),队列里保存活结点,每次出队的元素为扩展结点,扩展结点发散到的新结点将入队到队列。算法开始时把起点加入队列,循环直到队列为空,即可找到最优路线。如果采用优先队列,每次出队的元素为
f
(
n
)
f(n)
f
(
n
)
值最小的结点,这样会大大减小搜索范围。在下面的
搜索过程图示
可以直观地感受到使用优先队列和普通队列的区别。
如何构造
h
(
n
)
h(n)
h
(
n
)
要构造
h
(
n
)
h(n)
h
(
n
)
首先要定义任意两个结点的距离,不能像Dijkstra那样用没有定义任意两点距离的抽象的图
(Dijkstra算法用的图最多邻接矩阵带有权值,但即使是这样,也只是在“能直接到达的两个点之间”定义了距离,不能直接到达而是需要中转的两个点之间并没有定义距离)
。
为了简化,使用格子地图,则
h
(
n
)
h(n)
h
(
n
)
可以构造为:
一、欧氏距离
最简单的就是直接用欧式距离估计结点n到终点的距离,这样对于格子地图必定满足
h
(
n
)
≤
h
∗
(
n
)
h(n) \leq h^*(n)
h
(
n
)
≤
h
∗
(
n
)
,首选。
二、曼哈顿距离
对于规定不能斜着走的格子地图,用曼哈顿距离(两点X差的绝对值+Y差的绝对值)也是可以的。但是如果地图可以斜着走,就不能保证
h
(
n
)
≤
h
∗
(
n
)
h(n) \leq h^*(n)
h
(
n
)
≤
h
∗
(
n
)
了,不过可以采用除以
2
\sqrt{2}
2
的方式保证
h
(
n
)
≤
h
∗
(
n
)
h(n) \leq h^*(n)
h
(
n
)
≤
h
∗
(
n
)
必定满足。
三、其他
其他任何满足
h
(
n
)
≤
h
∗
(
n
)
h(n) \leq h^*(n)
h
(
n
)
≤
h
∗
(
n
)
的距离都可以选用。
关于
g
(
n
)
g(n)
g
(
n
)
把
g
(
n
)
g(n)
g
(
n
)
作为一个属性
(比如我用cost表示这个属性)
绑定在结点n里即可,寻路算法开始前设置所有的结点的cost设为
+
∞
+\infty
+
∞
(实际编程里用负数表示
+
∞
+\infty
+
∞
,常用-1表示)。在寻路开始时,先把起点的cost设为0,然后从起点开始发散的过程中,如果是直着(上、下、左、右)从格子A到下一个格子B,则到达的那个格子B的cost设置为A的
c
o
s
t
+
1
cost+1
c
o
s
t
+
1
,如果是斜着(左上方、左下方、右上方、右下方)从格子A到下一个格子B,则到达的那个格子B的cost设置为A的
c
o
s
t
+
2
cost+\sqrt{2}
c
o
s
t
+
2
即可完成支持直走和斜走的cost的迭代,函数
g
(
n
)
g(n)
g
(
n
)
只需要返回n的cost即可。
路况设置如何实现
就是上述的cost+1改成
c
o
s
t
+
1
×
c
o
n
d
i
t
i
o
n
cost+1 \times condition
c
o
s
t
+
1
×
c
o
n
d
i
t
i
o
n
,把上述的
c
o
s
t
+
2
cost+\sqrt{2}
c
o
s
t
+
2
改成
c
o
s
t
+
2
×
c
o
n
d
i
t
i
o
n
cost+\sqrt{2} \times condition
c
o
s
t
+
2
×
c
o
n
d
i
t
i
o
n
,其中condition是要到达的位置的路况。
然后要修改
h
(
n
)
h(n)
h
(
n
)
,在原先返回的
h
(
n
)
h(n)
h
(
n
)
的基础上乘整个地图的最小的condition,这样就能保证对于任何一个n仍然满足
h
(
n
)
≤
h
∗
(
n
)
h(n) \leq h^*(n)
h
(
n
)
≤
h
∗
(
n
)
,这样即可在设置不同路况的情况下还能保证能解得最优解。
完整的流程
“伪代码”如下:
[准备格子地图,设置h(n)并且f(n)=g(n)+h(n)]
|
|算法开始
v
[输入起点b和终点e,设置当前已经得到的临时最优解对应的代价M=正无穷]
|
v
[构造一个优先队列Q元素为结点(Node*),结点拥有属性double cost、Node *prior和double condition,每次出队的结点n为f(n)值最小的]
|
|初始化所有结点的cost为正无穷(代码实现起来是-1),prior为NULL,condition是路况
|
v
[b入队到Q]
|
|<--------------------------------------
| 真|
v 真 | 假
[Q不为空?] -------->[Q出队一个元素i]-->[f(i)>=M?]------->[i往8个方向发散,记8个方向在数组里t[8]; j=0]
| ^ |
| | 假 v ++j
| ---------------------------------------------------------------------- [j<8?] <-------------------------
| | |
|假 |真 ^
| v 假 |
| [i->cost+d(i, t[j]) < t[j]->cost ? (d(i, t[j])如果i和t[j]是直着的是1,如果i和t[j]是斜着的是根号2)]-->---|
| |真 |
| v ^
| [设置t[j]->cost = i->cost+d(i, t[j])*t[j]->condition; 设置t[j]->prior = i] |
| | |
| v 假 |
| [t[j]是e? (如果使用的是拷贝的地图数据则考虑t[j]和e坐标是否相同)] ------>[t[j]入队到Q]------------>------
| |真 |
| v ^
| [设置M = t[j]->cost]----------------->-------------------------------------
|
| ----------------------------
| | |
v 真 v |
[e->prior!=NULL?]------->[构造一个栈R,设置结点指针i=e]----->[i==NULL?]------->[i入栈到R; i=i->prior]
| 真| 假
|假 |
v v
[无解,b和e之间是不连通的] [返回R,R的出栈顺序即为从b到e的路径]
上面的“伪代码”乱得我自己都不想看。。。下面来个Flowchart流程图表述流程吧:
搜索过程图示
下面展示搜索过程动画的工具是我在写完A*算法后觉得挺有意思然后进一步写的一个GUI程序,在后面的
GUI程序下载链接
可以下载。
允许斜走,使用优先队列

禁止斜走,使用优先队列

允许斜走,使用普通队列

禁止斜走,使用普通队列

可以看到,用优先队列会减少很多不必要的搜索区域。我是先录屏,然后上面两张图片是用ps转换为gif的,下面两张因为时间比较长,用ps储存为web格式的时候内存爆了,所以下面两张是用格式工厂转换的,画质极差,将就着看吧。
核心代码
由于代码较长,不能折叠显示,这里只贴出部分代码,完整代码见:
https://github.com/Eyre-Turing/a_star
结点展开的循环
//isRunnable是一个bool变量,如果要中止寻路,则可以通过在其他的线程把isRunnable设置为false实现。
//aliveNodeP是一个优先队列
//handleAliveNodeCallBack是一个回调函数,用于给GUI程序等提供显示路径搜索过程使用。
//MapPos是一个结构体,保存地图的一个点的坐标(r, c)、已经消耗的代价(cost)以及代价估计(lowerBound)
//searchOne是把一个结点往四周展开(如果支持斜着走就是八方向展开,否则是四方向展开)
//matrix是地图,其get方法是获取一个结点指针(MapNode*),MapNode的isInAliveNodes属性保存该结点的坐标(MapPos)是否在aliveNodeP里存在,目的是去除重复展开。
while(isRunnable && !aliveNodeP.empty())
{
MapPos handleAliveNode = aliveNodeP.top();
aliveNodeP.pop();
if(handleAliveNodeCallBack)
{
handleAliveNodeCallBack(this, handleAliveNode);
}
searchOne(handleAliveNode.r, handleAliveNode.c, handleAliveNode.lowerBound);
matrix->get(handleAliveNode.r, handleAliveNode.c)->isInAliveNodes = false;
}
while(!aliveNodeP.empty())
{
MapPos handleAliveNode = aliveNodeP.top();
aliveNodeP.pop();
matrix->get(handleAliveNode.r, handleAliveNode.c)->isInAliveNodes = false;
}
代价估计函数
f
(
n
)
f(n)
f
(
n
)
/*
* 从起点经过当前点[r][c],再到终点,路径长度的一个下界
* 如果这个下界小于当前已经得到的解,认为是有希望比当前已经得到的解更优的
* 如果这个下界大于或等于已经得到的解,则这条路不必再展开搜索了
* -1认为是正无穷(或者是负数认为是正无穷)
*/
double AStar::lowerBoundFunction(int r, int c) const
{
//minCondition是地图里最小的路况,如果最小路况为正无穷(代码表示为负数),就返回正无穷(代码表示为-1)。
//endR和endC为终点的位置坐标,endR为Y值,endC为X值。
if(minCondition < 0)
{
return -1;
}
if(isObliqueEnable)
{
return matrix->get(r, c)->cost+sqrt(pow(r-endR, 2)+pow(c-endC, 2))*minCondition; //下界为:已走路程+最小路况下当前点到终点的欧氏距离
}
else
{
return matrix->get(r, c)->cost+(fabs(r-endR)+fabs(c-endC))*minCondition; //下界为:已走路程+最小路况下当前点到终点的曼哈顿距离
}
}
GUI程序下载链接
Windows:
http://eyre-turing.top/project/get_data/a_star.exe
Linux x64:
http://eyre-turing.top/project/get_data/a_star
给两幅测试地图
一、
点我下载简单迷宫
效果如下:

二、
点我下载复杂迷宫
效果如下:

该地图我没有设置起点和终点位置,你可以自己随便设置。
GUI程序使用说明
宽度
、
高度
编辑框设置地图的大小,
尺寸
设置每个格子的边长占多少个像素。修改了这些参数后要点击
确认修改
才会生效。
勾选
编辑模式
即可编辑墙壁以及路况,编辑模式下在地图空白处点击左键即可添加墙,在墙处点击左键即可移除墙(地图界面中黑色的是墙)。编辑模式下,对空白处右键即可设置路况,右键后选中的格子会有黄色边框,黄色边框出现后,在
路况
编辑框填入数字即可调整选中格子的路况,路况值越大表示该位置越拥堵。
点击
设置起点
后即可在地图上标记起点位置,
起点
是绿色格子;点击
设置终点
后即可在地图上标记终点位置,
终点
是红色格子。
勾选显示网格后会画出地图所有格子的边框。
勾选
允许斜走
即可八方向发散搜索路线,勾选
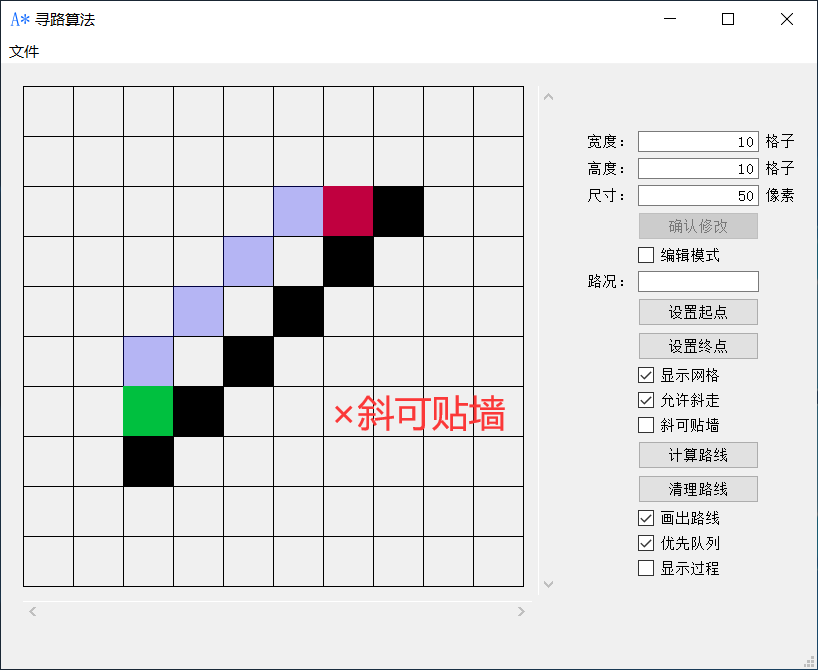
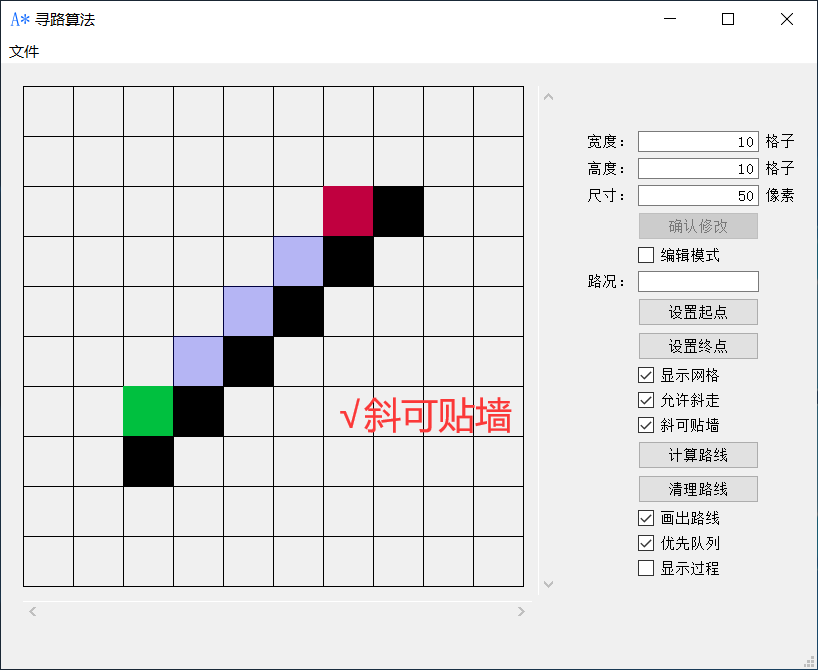
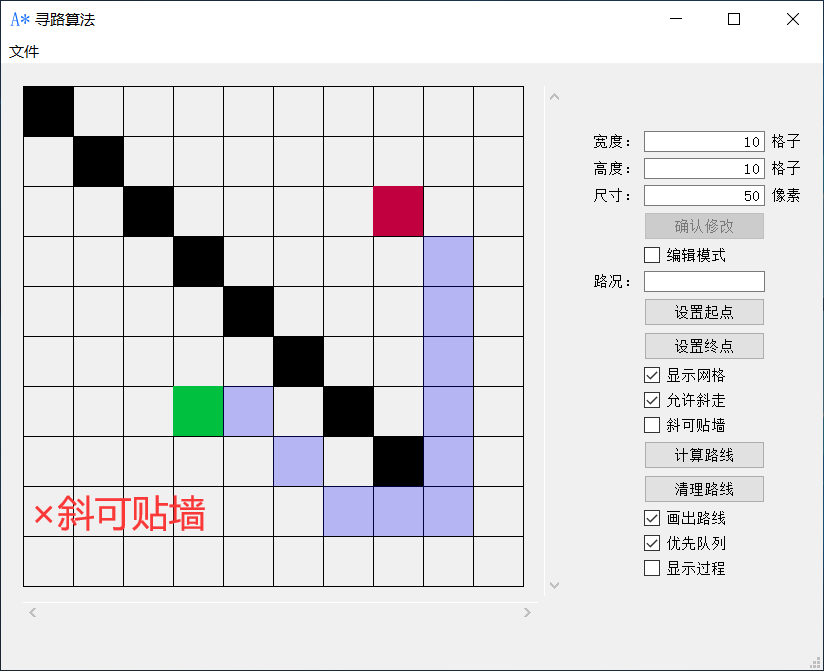
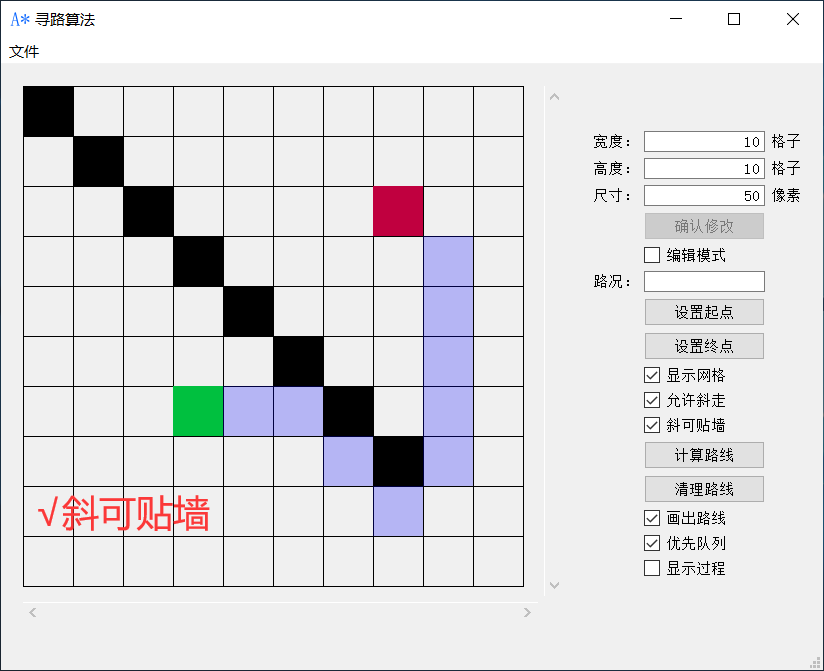
斜可贴墙
即可斜走的情况下贴着墙走。
点击
计算路线
即可开始运行A*算法搜索路径,点击
清理路线
即可消除计算出来的路线,在开始寻路的时候,清理路线按钮会变成
计算中止
按钮,点击即可中止寻路。
勾选
画出路线
即可在搜索出路径后在地图上画出来。
勾选
优先队列
即使用优先队列来保存活结点队列。
勾选
显示过程
即可在计算路线时动画显示出搜索路线的过程,勾选后会在下方显示一个文本编辑框,该编辑框可以设置动画显示的速度。
菜单栏的
文件
可以展开以执行
读取
地图和
保存
地图的操作。