博客

题目来源

• 
  牛客网：HJ16 购物单
  

题目描述

题目解析

我们可以这样理解，对于同一个物品，它的价格、重要度都是可变的。那么我们只需要对每一个主件尝试如下四种情况：

• 仅加入一个主件
• 加入主件和第一个附件
• 加入主件和第二个附件
• 加入主件和两个附件

在如上四种情况中找到最大值就是01背包问题了

对于一个可承重C的背包，我们假设所有物品的重量数据保存在w[]，所有价值数据保存在v[]。那么我们有如下推导式：



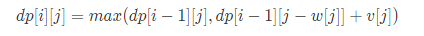
那么对于“购物单”这道题，我们可以有如下抽象：

因此，我们先画出这样的表

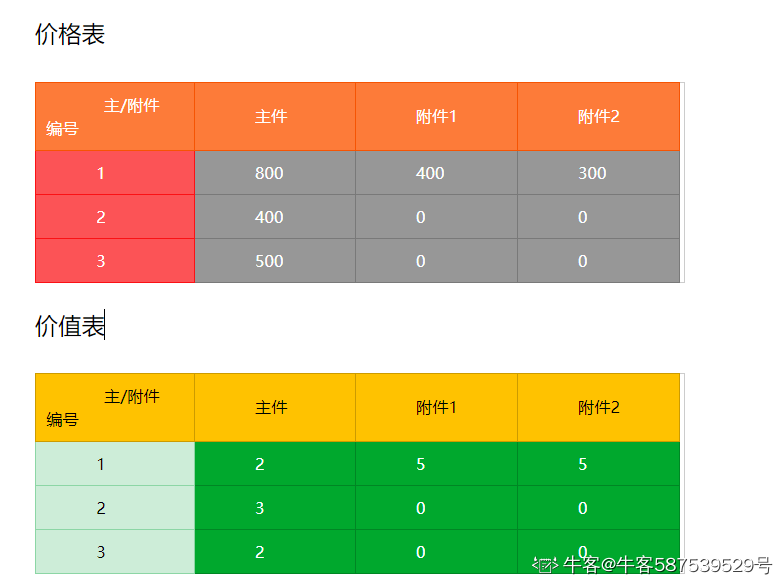
#include <iostream>
#include <vector>
#include <algorithm>
 
using namespace std;

int main(){
    int M,N;
    cin>>M>>N;
    M /= 10; // 由于所有的价格都是10的整倍数，所以可以均除10以简化运算复杂度
    vector<vector<int>> prices(N+1,vector<int>(3,0));
    vector<vector<int>> values(N+1,vector<int>(3,0));
    for (int i = 1; i <= N; ++i) {
        int price, priority, hasAttach;
        cin >> price >> priority >> hasAttach;
        if(hasAttach == 0){
            prices[i][0]=price/10;
            values[i][0]=priority;
        }else {
            if(prices[hasAttach][1] != 0){
                prices[hasAttach][2] = price / 10;
                values[hasAttach][2] = priority;
            }else{
                prices[hasAttach][1] = price / 10;
                values[hasAttach][1] = priority;
            }
        }
    }

    vector<vector<int>> dp(N+1,vector<int>(M+1,0));
    for(int i=1;i<=N;i++){
        for(int j=1;j<=M;j++){
            int a=prices[i][0],b=values[i][0];
            int c=prices[i][1],d=values[i][1];
            int e=prices[i][2],f=values[i][2];
            dp[i][j]=j>=a?max(dp[i-1][j-a]+a*b,dp[i-1][j]):dp[i-1][j];
            dp[i][j]=j>=a+c?max(dp[i-1][j-a-c]+a*b+c*d,dp[i][j]):dp[i][j];
            dp[i][j]=j>=a+e?max(dp[i-1][j-a-e]+a*b+e*f,dp[i][j]):dp[i][j];
            dp[i][j]=j>=a+c+e?max(dp[i-1][j-a-e-c]+a*b+c*d+e*f,dp[i][j]):dp[i][j];
        }
    }
    cout<<dp[N][M]*10<<endl;
}