什么是
l
o
w
b
i
t
lowbit
l
o
w
b
i
t
?
学习树状数组之前我们首先要知道什么是
l
o
w
b
i
t
lowbit
l
o
w
b
i
t
,
l
o
w
b
i
t
(
x
)
lowbit(x)
l
o
w
b
i
t
(
x
)
表示
x
x
x
在
2
2
2
进制下最低位的
1
1
1
以及它后面的
0
0
0
所表示的二进制数。例如
l
o
w
b
i
t
(
3
)
=
1
,
l
o
w
b
i
t
(
2
)
=
2
lowbit(3)=1,lowbit(2)=2
l
o
w
b
i
t
(
3
)
=
1
,
l
o
w
b
i
t
(
2
)
=
2
。
怎么迅速地求出
l
o
w
b
i
t
lowbit
l
o
w
b
i
t
呢?这里有一条简单的公式:
l
o
w
b
i
t
(
x
)
=
x
&
−
x
lowbit(x)=x \& -x
l
o
w
b
i
t
(
x
)
=
x
&
−
x
树状数组的定义
树状数组中的每一个节点都表示它相应区间的一个值(区间和,区间最大值等,可以自己决定,以下都用区间和作为例子),比如
C
x
C_x
C
x
表示从
x
x
x
这个节点开始向前
l
o
w
b
i
t
(
x
)
lowbit(x)
l
o
w
b
i
t
(
x
)
个节点中这个区间的和如下图所示:
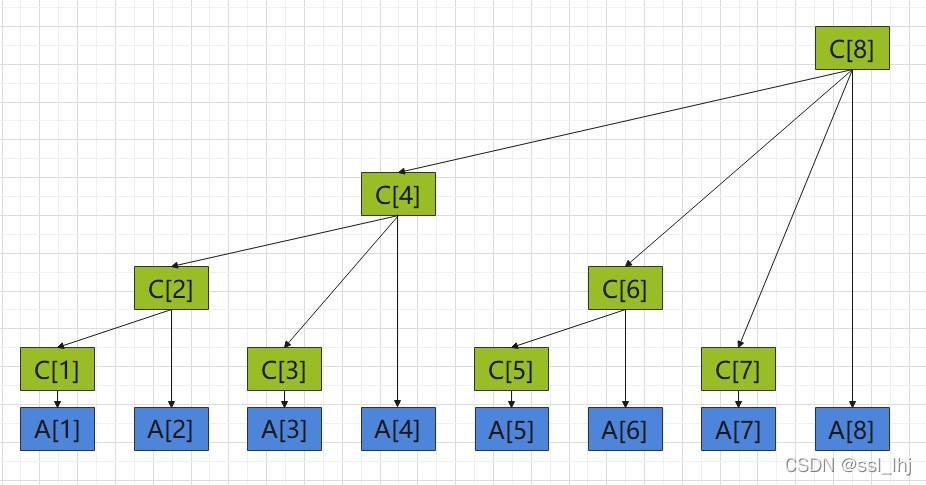
该图表示了树状数组与原数组之间的关系,我们可以将
1
,
4
,
7
,
3
,
2
,
8
,
6
,
10
1,4,7,3,2,8,6,10
1
,
4
,
7
,
3
,
2
,
8
,
6
,
1
0
代入原序列
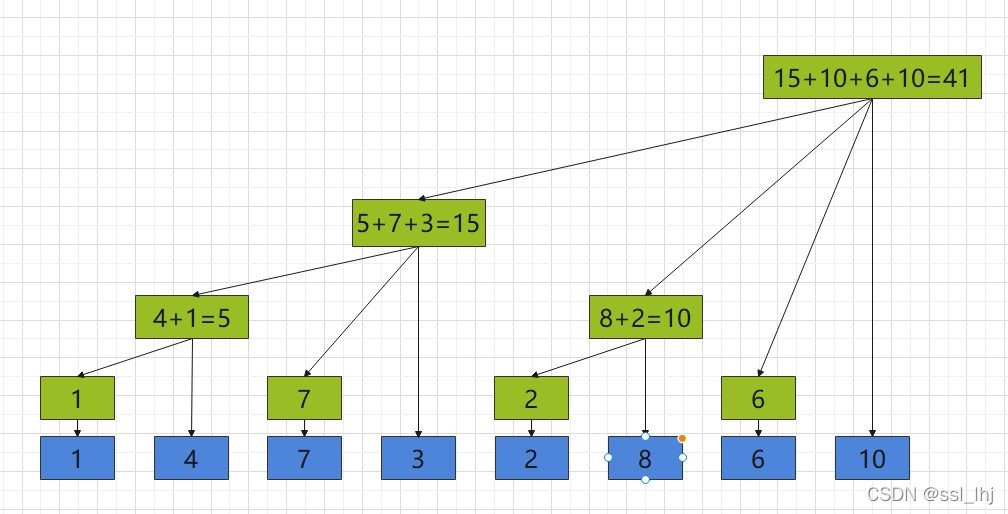
这样就很清楚了吧,树状数组的表示方法一目了然。
树状数组的性质:
-
Cx
C_x
C
x
表示以它为根的子树的所有子树的和比如
C2
=
C
1
+
A
2
C_2=C_1+A_2
C
2
=
C
1
+
A
2
(不重复计算
A1
A_1
A
1
) -
Cx
C_x
C
x
的父节点是
Cx
+
l
o
w
b
i
t
(
x
)
C_{x+lowbit(x)}
C
x
+
l
o
w
b
i
t
(
x
)
-
Cx
C_x
C
x
的总叶节点个数(也就是表示的区间长度)等于
lo
w
b
i
t
(
x
)
lowbit(x)
l
o
w
b
i
t
(
x
)
单点修改区间查询
单点修改
单点修改时,只会影响到它到根节点的这条路径上的所有节点,再根据树状数组的性质
2
2
2
我们可以得到单点修改函数:
//给第x个节点加上y
inline void xg(ll x,ll y){
for(;x<=n;x+=lb(x))//枚举从当前节点到根节点
c[x]+=y;//逐一修改
}
区间查询
求前缀和
树状数组还可以用来求前缀和,把每个不相交区间内的
C
C
C
都相加就可以得到前缀和了
//求前x个数的和
inline ll qz(int x){
ll ans=0;for(;x;x-=lb(x))ans+=c[x];
return ans;
}
区间求和
将两个端点的前缀和相减就可以得到区间和了
inline ll qz(int x){
ll ans=0;for(;x;x-=lb(x))ans+=c[x];
return ans;
}
inline ll sch(int l,int r){
return (qz(r)-qz(l-1));
}
区间修改单点查询
分析
由于树状数组不是线段树,所以不能像上面那样维护区间和了,我们要维护差分值,让
C
x
=
A
x
−
A
x
−
1
(
A
0
=
0
)
C_x=A_x-A_{x-1}(A_0=0)
C
x
=
A
x
−
A
x
−
1
(
A
0
=
0
)
这样,区间修改时,只要修改区间两端的差分值就能做到修改整个区间。
inline void xg(ll x,ll y){
for(;x<=n;x+=lb(x))
c[x]+=y;
}
inline void add(ll l,ll r,ll x){
xg(l,x);xg(r+1,-x);//左端点差值增加
}
那么怎么单点查询呢?
很明显,当用一个差分序列表示另一个序列时,
A
x
=
∑
i
=
1
i
=
x
A_x=\sum_{i=1}^{i=x}
A
x
=
∑
i
=
1
i
=
x
用树状数组求前缀和就好了
inline ll sch(ll x){
ll ans=0;for(;x;x-=lb(x))ans+=c[x];
return ans;
}