也许大家会疑问:复习完栈应该到队列了吧。我开始也是这样想的,但用栈实现递归,是一个难点。说实话,我以前学习的时候,就在这一处卡住了,当时我烦躁了好几天,但可能由于突然被什么东西转移了注意力,所以就这样跳过去了。不知道用栈实现递归,也确实不大影响后面的学习,但我可以肯定,如果你觉得世界上有一些东西难以理解而不愿面对,那自信将会由此削弱。当然,遇到困难可以适当地把它放下,但逃避应该是暂时的,必须鼓励自己――-也许是几天,也许是几个月――但绝对要攻克它!
void
TOH(
int
n, Pole start, Pole goal, Pole temp)
//
把n个圆盘从start柱移到goal柱,temp柱作为辅助柱
{
if
(n
==
0
)
return
;
//
base case
TOH(n
–
1
, start, temp, goal);
//
把n-1个圆盘从start柱移到temp柱,goal作为此次的辅助柱
move(start,goal);
//
从start柱移动一块圆盘到goal柱
TOH(n
–
1
, temp, goal, start);
//
把temp柱中的n-1个圆盘移到goal柱
return
;
}
1、
如果你可以把一个任务分解成更小的几个子任务,你便可以把这些分解后的子任务,留给别人去做。
2、
当你把任务分解后,你必须把这些子任务,分别写在任务纸上,并按照这些子任务的执行顺序,从后到先,依次叠放在那张办公桌上,即保证最上面的那张纸,就是应该最先执行的任务。
通常(因为还有一种特别情况,将下面给出),每个员工只需负责办公桌上,放在最上面的那张纸上的任务。
如果你无法再分解这个任务,你就要亲自完成这个任务,并且如果办公桌上还有任务纸,那你必须继续处理下一张任务纸。
#include
<
很兴奋,经过刚才的思考:我先是在草稿纸上进行了一些“画画”的工作,当我把用栈实现汉诺塔的搬运过程,一步步地的画在纸上的时候,思维由这些具体的步骤而变得清晰起来(“画画”确实是一种有助于思考的方法。很可惜我没有扫描工具,否则我可以把这些画插在我这篇文章中,将会非常生动)。然后我想到一个不错的比喻来帮助自己理解这一个过程。这一个比喻,我非常得意,一会与大家分享。现在,我自认为把这个问题完全攻克了(请大家原谅我的自恋^_^),所以才迫不及待地要把思考的结果写下来。
我还是按书上那个汉诺塔的例子来表述这个思想,而且把汉诺塔的递归用栈实现,也恰好有一定的难度。但我建议,大家看完我这篇文后,不妨试着一个递归用栈去实现一下,很容易就检验出你是否真的领会了其中的思想。
-、汉诺塔问题:
有三根柱子分别叫A柱、B柱、C柱。现假设有N个圆盘(都是按从大到小依次放入柱中的)已经放在了A柱上,我们的任务就是把这N个圆盘移动到C柱。但移动的过程,必须遵守大盘永远在小盘的下面这一个原则。
二、移动汉诺塔的递归思想:
1、
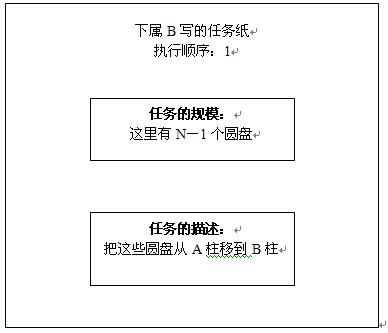
先把A柱上面的(N-1)个圆盘移到B柱(这一步使问题的规模减少了1)。
先把A柱上面的(N-1)个圆盘移到B柱(这一步使问题的规模减少了1)。
2、
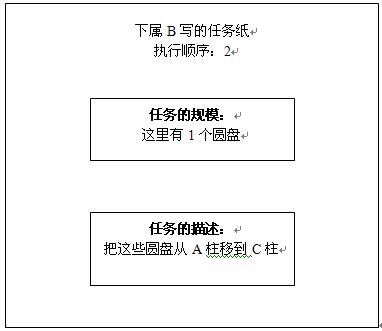
再把A柱上剩下的那个最大的圆盘移到C柱。
再把A柱上剩下的那个最大的圆盘移到C柱。
3、
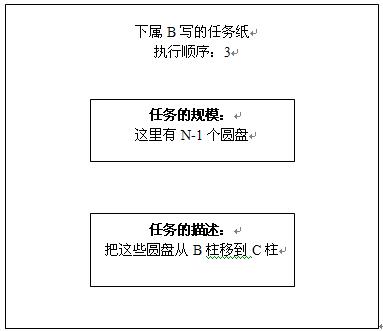
最后把B柱上的(N-1)圆盘移到C柱。
最后把B柱上的(N-1)圆盘移到C柱。
当我们写递归函数的时候,我们先假设我们即将写的这个函数已经能解决n个圆盘的汉诺塔问题了,递归就是这样一种思想:它告诉我们程序员,做梦也是一件有意义的事^_^。那么我们现在假设这个函数的接口是这样的:
Void TOH(int n, Pole start, Pole goal, Pole temp )(第一次调用时,我们是这样用这个函数的:
Void TOH(N, A, C, B);N是圆盘数、A是起始柱、B是暂时柱、C是目标柱。)然后,我就利用上面分析的递归步骤(当然,递归中的初始情况base case也是不能忘记的),在该函数体里面,继续调用该函数,便得到了递归函数:
void
TOH(
int
n, Pole start, Pole goal, Pole temp)
//
把n个圆盘从start柱移到goal柱,temp柱作为辅助柱
{
if
(n
==
0
)
return
;
//
base case
TOH(n
–
1
, start, temp, goal);
//
把n-1个圆盘从start柱移到temp柱,goal作为此次的辅助柱
move(start,goal);
//
从start柱移动一块圆盘到goal柱
TOH(n
–
1
, temp, goal, start);
//
把temp柱中的n-1个圆盘移到goal柱
return
;
}
三、用栈实现递归的思想:
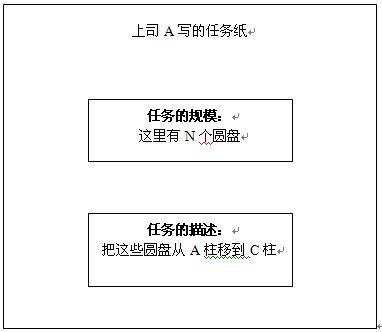
现在,我将用一个自认为得意的比喻,来表达这个思想。我们不妨设想有这样一个环境:有一家独特的公司,这家公司的上司是这样给他们的下属分配任务的:当有一个任务来临的时候,一位上司就会把这个任务写在一张格式统一的纸上(这张纸象征着栈中的一个元素,但纸上的内容与栈中元素的内容会有一些差异),这张纸上一般会记录下面这两个信息:

这位上司A会把这张
任务纸
放到公司里一张专门的办公桌上(它是栈的象征)。
任务纸
放到公司里一张专门的办公桌上(它是栈的象征)。
好了,现假设,上司A把这张任务纸放在了那张专门的办公桌上,一个下属B查看办公桌时,发现了这个任务。他并没有立刻就去执行这个任务,因为他们公司有一个奇怪但令人鼓舞的规定:
1、
如果你可以把一个任务分解成更小的几个子任务,你便可以把这些分解后的子任务,留给别人去做。
2、
当你把任务分解后,你必须把这些子任务,分别写在任务纸上,并按照这些子任务的执行顺序,从后到先,依次叠放在那张办公桌上,即保证最上面的那张纸,就是应该最先执行的任务。
那么下属B发现,他可以把上司A写在那张纸上的任务分解成三个子任务:



然后,B把这三张纸依次从上到下地叠放在办公桌上,那么他可以下班了^_^。
之后,下属C来上班,发现了办公桌上叠放了三张纸,注意,公司有如下规定:
通常(因为还有一种特别情况,将下面给出),每个员工只需负责办公桌上,放在最上面的那张纸上的任务。
C拿起最上面那张纸,就是B写的执行顺序为1的那张纸,他立刻笑了。他也模仿B,把这个任务分解成:
1、
这里有N-2个圆盘,把这些圆盘从A柱移到C柱。
这里有N-2个圆盘,把这些圆盘从A柱移到C柱。
2、
这里有1个圆盘,把这个圆盘从A柱移到B柱。
这里有1个圆盘,把这个圆盘从A柱移到B柱。
3、
这里有N-2个圆盘,把这些圆盘从C柱移到B柱。
这里有N-2个圆盘,把这些圆盘从C柱移到B柱。
然后,他把三个子任务的三张任务纸替换掉B写的那张纸。那么他又可以下班了。
就这样,员工们很轻松的工作。直到有一个员工,假设他名叫X,比较不幸,他发现办公桌上最上面的那张纸上写着:把一个圆盘从某根柱移到另一根柱。因为这个任务根本就没办再分了,所以可怜的X就只好亲自动手去完成这个任务,但事情并没有结束,因为该公司规定:
如果你无法再分解这个任务,你就要亲自完成这个任务,并且如果办公桌上还有任务纸,那你必须继续处理下一张任务纸。
正如前面所说,办公桌上的纸的处理方式,就是栈的后进先出的方式,而任务纸就是栈的元素。这应该很容易理解。难点在于两点:
1、
栈元素的内部结构如何定义?我们可以把栈元素看作一个结构体,或者看作一个类对象,而任务的规模应该是类对象的一个整形数据成员,但任务描述,就不太好处理了。事实上,我们可以对任务进行分类,然后只要用一个枚举类型或是其他数据类型,来区分这个任务属于哪种分类。
栈元素的内部结构如何定义?我们可以把栈元素看作一个结构体,或者看作一个类对象,而任务的规模应该是类对象的一个整形数据成员,但任务描述,就不太好处理了。事实上,我们可以对任务进行分类,然后只要用一个枚举类型或是其他数据类型,来区分这个任务属于哪种分类。
2、
如何把上面所分析的过程,用程序表达出来?好了,如果你耐心的阅读了上面的文字,那么理解下面这个程序,应该非常容易了:
如何把上面所分析的过程,用程序表达出来?好了,如果你耐心的阅读了上面的文字,那么理解下面这个程序,应该非常容易了:
我对书中的程序稍作改写,也作更丰富的注释,读程序的时候,注意联系我上文所作的比喻:
#include
<
版权声明:本文为chinainvent原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。