7.1 无向树及生成树
先来看一些基本概念:
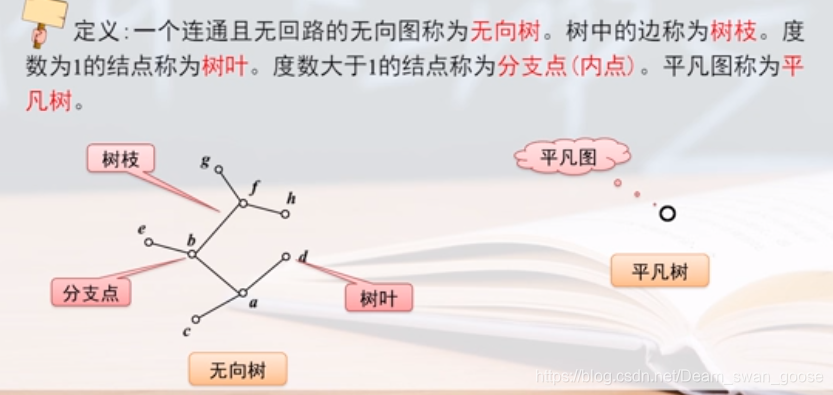
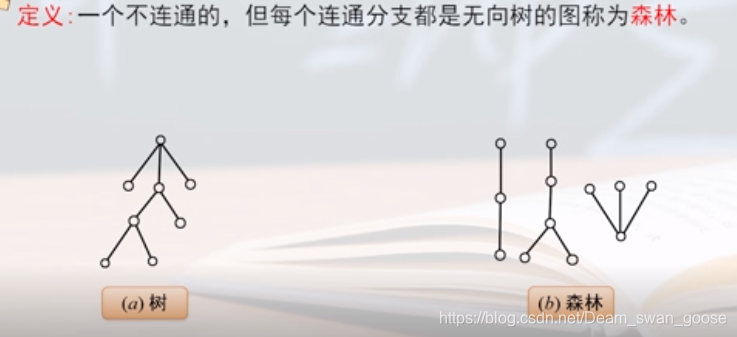
简单来说就是由多颗数组成的。
来看一些定理:

如果我们让树中的每一条与其下方的结点对应,那么最后多出来一个根节点。故在树中,边数等于结点数减去1。
定理2:

例题:
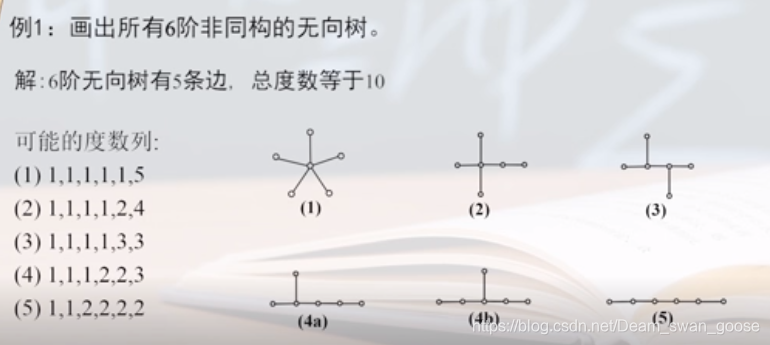

解析:
由上可知,树中结点数减去1就是边数,边数乘以2就是总度数。根据这个可以列方程求解。

生成树:删回路,直到出现树
弦:把生成树抠掉剩下的边角料
余树:边角料的集合
注意:
- 余树可以不连通,且可能含有回路。
- 生成树一般不是唯一的,只有当图是一棵树时,其生成树才是唯一的。(也就是说:生成树的唯一性不确定)

我们来看最小生成树:

来看一个算法:

例题:
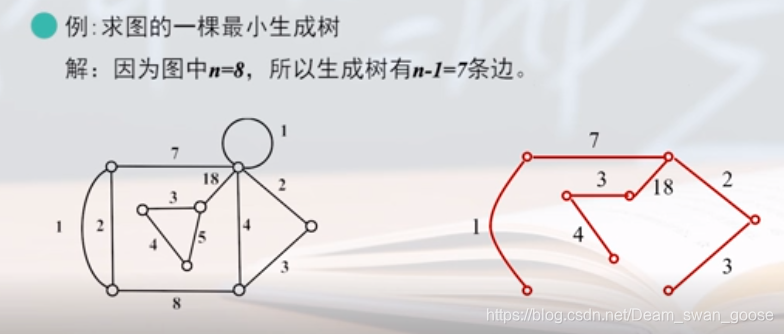
弦的基本回路:
对于每一条弦
e
e
e
,存在唯一的由弦
e
e
e
和生成树的树枝构成的初级回路
C
e
C_e
C
e
,称
C
e
C_e
C
e
为对应于弦
e
e
e
的
基本回路
。所以基本回路的集合称为生成树
T
T
T
的
基本回路系统
。
eg:
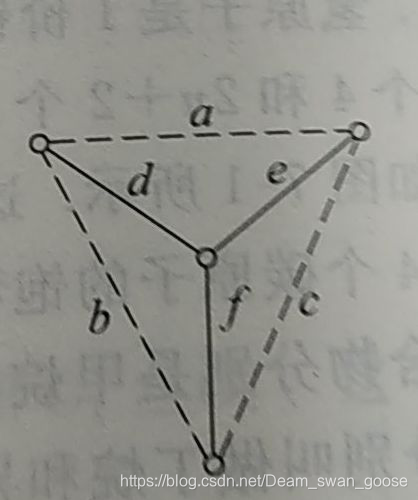
C
a
C_a
C
a
= aed
C
b
C_b
C
b
= bdf
C
c
C_c
C
c
= cef
基本回路系统为:
{
C
a
C_a
C
a
,
C
b
C_b
C
b
,
C
c
C_c
C
c
}
树枝的基本割集:
对于生成树的每一个树枝
a
a
a
,存在唯一的由树枝
a
a
a
其余边都是弦的割集
S
a
S_a
S
a
,称
S
a
S_a
S
a
为对应树枝
a
a
a
的
基本割集
,称所有基本割集的集合为对应生成树
T
T
T
的
基本割集系统
。
eg:
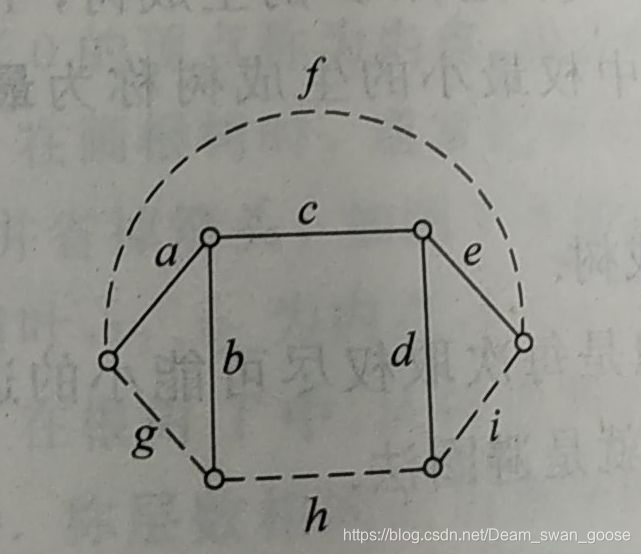
S
a
S_a
S
a
= {a,g,f}
S
b
S_b
S
b
= {b,g,h}
S
c
S_c
S
c
= {c,f,h}
S
d
S_d
S
d
= {d,h,i}
S
e
S_e
S
e
= {e,f,i}
基本割集系统为{
S
a
S_a
S
a
,
S
b
S_b
S
b
,
S
c
S_c
S
c
,
S
d
S_d
S
d
,
S
e
S_e
S
e
}
合并:操作方法就是将
C
i
C_i
C
i
和
C
j
C_j
C
j
中相同的删除再合并起来。
eg;

易得:
C
f
C_f
C
f
= face
C
g
C_g
C
g
= gba
C
h
C_h
C
h
= hdcb
C
i
C_i
C
i
= ied
C
f
C_f
C
f
⨁
\bigoplus
⨁
C
g
C_g
C
g
= fgbce
C
f
C_f
C
f
⨁
\bigoplus
⨁
C
h
C_h
C
h
= fabhde
⋯
\cdots
⋯
练习1:
设图G是有6个顶点的连通图,总度数为20,则从G中删去()条边后使之变成树?
练习2:
设G是一棵树,则G的生成树有()棵?
答案:1
练习3:
设G是一棵无向树,则G一定是()?


解析:
让树的每一层的点交替属于
v
1
v_1
v
1
,
v
2
v_2
v
2
即可。
练习4:
