传送门
A. Love Story
signed main()
{
IO;
int t;cin >> t;
string ss = "codeforces";
while(t--)
{
string s;cin >> s;
int cnt = 0;
for(int i = 0;i < 10;i ++)
{
if(s[i] != ss[i])
cnt ++;
}
cout << cnt << endl;
}
return 0;
}
B. Blank Space
signed main()
{
IO;
int t; cin >> t;
while (t--)
{
int n; cin >> n;
vector<int> a(n);
int ans = 0, cnt = 0;
for (int i = 0; i < n; i++)
{
cin >> a[i];
if (a[i] != 0) {
ans = max(ans, cnt);
cnt = 0;
}
else
cnt++;
}
ans = max(ans, cnt);
cout << ans << endl;
}
return 0;
}
C. Mr. Perfectly Fine
题意:有
n
n
n
本书,每本书可以使你学会
a
a
a
技能或
b
b
b
技能,或者同时学会
a
,
b
a, b
a
,
b
技能。看每本书都有对应的代价,求学会两种技能的最小代价
思路:将书分为只学会
a
a
a
技能和只学会
b
b
b
技能和同时学会
a
b
ab
ab
技能,三种类型,用
3
3
3
个变量维护三种类型各自的最小代价,最后得到答案。
signed main()
{
IO;
int t; cin >> t;
while (t--)
{
int n;cin >> n;
int cnt1 = oo, cnt2 = oo, cnt3 = oo;
for(int i = 1;i <= n;i ++)
{
int ti;cin >> ti;
string k;cin >> k;
if(k[0] == '1' && k[1] != '1')
cnt2 = min(cnt2, ti);
if(k[0] == '1' && k[1] == '1')
cnt1 = min(cnt1, ti);
if(k[0] != '1' && k[1] == '1')
cnt3 = min(cnt3, ti);
}
int ans = min(cnt1, cnt2 + cnt3);
if(ans >= oo)
cout << -1 << endl;
else
cout << ans << endl;
}
return 0;
}
D. Gold Rush
题意:有一堆
n
n
n
个金币,没次操作可以将其分为
a
,
b
a,b
a
,
b
两堆,但是二者数量的比值必须为
2
:
1
2:1
2
:
1
,问能否通过一系列操作得到个数为
m
m
m
的堆
思路:
n
∗
(
1
3
)
p
∗
(
2
3
)
q
=
m
n * (\frac{1}{3})^p * (\frac{2}{3})^q = m
n
∗
(
3
1
)
p
∗
(
3
2
)
q
=
m
显然
m
n
=
2
q
3
p
+
q
\frac{m}{n}=\frac{2 ^q}{3^{p+q}}
n
m
=
3
p
+
q
2
q
所以通分
m
/
n
m/n
m
/
n
,然后分解
m
,
n
m,n
m
,
n
的因子,如果
m
m
m
只包含因子
2
2
2
,
n
n
n
只包含因子
3
3
3
,且3的个数大于2的个数就有解
signed main()
{
IO;
int t; cin >> t;
while (t--)
{
int n, m;
cin >> n >> m;
int d = gcd(m, n);
int cnt2 = 0, cnt3 = 0;
m /= d, n /= d;
// cout << n << ' ' << m << endl;
while (m % 2 == 0)m /= 2, cnt2++;
while (n % 3 == 0)n /= 3, cnt3++;
if (m == 1 && m == n && cnt3 >= cnt2)
cout << "YES\n";
else
cout << "NO\n";
}
return 0;
}
E. The Lakes
纯bfs没什么其他的
#include <bits/stdc++.h>
#define oo 0x3f3f3f3f
#define ll long long
#define OO 0x3f3f3f3f3f3f3f3f
#define IO ios::sync_with_stdio(false);cin.tie(nullptr)
#define endl "\n"
#define int ll
const int N = 2e5 + 10, M = 2 * N;
using namespace std;
typedef pair<int, int> pii;
#define deb(i,x) if(int i==x) int k = 1;
#define all(x) x.begin(),x.end()
ll lowbit(ll x) { return x & -x; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
ll qmi(ll a, ll b, ll mod) {
ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; }
return res;
}
int g[1001][1001];
int vis[1001][1001];
int n, m;
int dx[4] = {0,0,-1,1};
int dy[4] = {1,-1,0,0};
int bfs(int x, int y)
{
int ans = 0;
queue<array<int, 2>> q;
q.push({x, y}), vis[x][y] = 1;
while(q.size())
{
auto t = q.front(); q.pop();
int x = t[0], y = t[1];
ans += g[x][y];
for(int i = 0;i < 4;i ++)
{
int xx = x + dx[i], yy = y + dy[i];
if(xx > n || xx < 1 || yy > m || yy < 1)continue;
if(vis[xx][yy]) continue;
if(g[xx][yy] > 0)
{
vis[xx][yy] = 1;
q.push({xx, yy});
}
}
}
return ans;
}
signed main()
{
IO;
int t; cin >> t;
while (t--)
{
cin >> n >> m;
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
cin >> g[i][j], vis[i][j] = 0;
int ans = 0;
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
{
if(!vis[i][j] && g[i][j] > 0)
ans = max(ans, bfs(i, j));
}
cout << ans << endl;
}
return 0;
}
F. Forever Winter
题意:有一个图,其根节点直接与
x
x
x
个节点相邻,而这
x
x
x
个节点每一个又都和
y
y
y
个节点相邻。给定图中的点数和边数和所有边。求
x
,
y
x,y
x
,
y
思路:先求出图的最长直经,找到直径的两个端点,和直径长度。直径的中点就是根节点,它的度数就是
x
x
x
,随便找个根节点直接相邻的节点
n
o
d
e
node
n
o
d
e
,其度数减一就是
y
y
y
#include <bits/stdc++.h>
#define oo 0x3f3f3f3f
#define ll long long
#define OO 0x3f3f3f3f3f3f3f3f
#define IO ios::sync_with_stdio(false);cin.tie(nullptr)
#define endl "\n"
#define int ll
const int N = 2e5 + 10, M = 2 * N;
using namespace std;
typedef pair<int, int> pii;
#define deb(i,x) if(int i==x) int k = 1;
#define all(x) x.begin(),x.end()
ll lowbit(ll x) { return x & -x; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
ll qmi(ll a, ll b, ll mod) {
ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; }
return res;
}
int n, m;
struct node
{
int v, ne;
}e[N];
int h[N] = { 0 }, tot = 0;
void add(int u, int v)
{
e[++tot] = { v, h[u] }; h[u] = tot;
}
int mx1 = 0, id1 = 1, id2;
void dfs(int u, int fa, int de)
{
if (de > mx1) mx1 = de, id1 = u;
for (int i = h[u]; i; i = e[i].ne)
{
int v = e[i].v;
if (v == fa)continue;
dfs(v, u, de + 1);
}
}
int k, to;
vector<int> ans, tt;
void dfs1(int u, int fa)
{
if (u == id2) { ans = tt;}
tt.push_back(u);
for (int i = h[u]; i; i = e[i].ne)
{
int v = e[i].v;
if (v == fa)continue;
dfs1(v, u);
tt.pop_back();
}
}
signed main()
{
IO;
int t; cin >> t;
while (t--)
{
tt.clear();
tot = 0;
id1 = 1, id2 = 1;
mx1 = 0;
cin >> n >> m;
for (int i = 1; i <= n; i++)h[i] = 0;
for (int i = 1; i <= m; i++)
{
int u, v; cin >> u >> v;
add(u, v), add(v, u);
}
dfs(1, 0, 0);
id2 = id1;
mx1 = 0;
dfs(id1, 0, 0);
int de = mx1 + 1;
k = de / 2 + 1;
dfs1(id1, 0);
to = ans[ans.size() / 2];
int x = 0;
for (int i = h[to]; i; i = e[i].ne)x++;
int y = 0;
for (int i = h[e[h[to]].v]; i; i = e[i].ne) y++;
cout << x << ' ' << y - 1 << endl;
}
return 0;
}
G. Hits Different
题意:有一个塔状结构如图
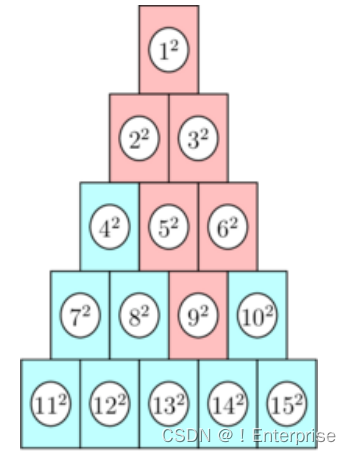
对于输入的
n
n
n
,求出直接或间接位于
n
n
n
上方所有部分的和,每部分都是形如
i
2
i^2
i
2
的值。
思路:记忆化+容斥
对于输入的
n
n
n
,可以用二分求出它所在的层数的上一层是第几层,令其为
k
k
k
。
然后就可以分3种情况得到直接位于它上方的部分的值。
- 第一种
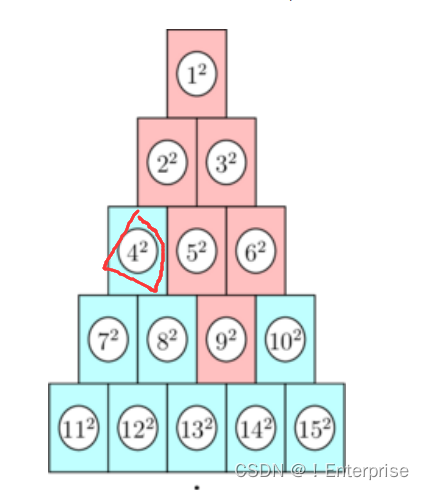
位于当前层的第一个,直接在其上方的部分就一个,值为
k
∗
(
k
+
1
)
/
2
−
k
+
1
k*(k + 1)/2-k+1
k
∗
(
k
+
1
)
/2
−
k
+
1
- 第二种
位于当前层最后一个,和第一种类似,其值为
k
∗
(
k
+
1
)
k*(k +1 )
k
∗
(
k
+
1
)
/2
- 第三种
位于当前层第
d
d
d
个
KaTeX parse error: Undefined control sequence: \and at position 9: d \ne 1 \̲a̲n̲d̲ ̲d\ne最后一个
,直接在其上方的有两个。分别为
k
∗
(
k
+
1
)
/
2
−
k
+
d
k*(k+1)/2-k+d
k
∗
(
k
+
1
)
/2
−
k
+
d
和
k
∗
(
k
+
1
)
/
2
−
k
+
d
−
1
k*(k+1)/2-k+d-1
k
∗
(
k
+
1
)
/2
−
k
+
d
−
1
int vis[N] = { 0 };
int get(int n)
{
int l = 1, r = 1e4;
while (l < r)
{
int mid = (l + r + 1) >> 1;
if ((mid + 1) * mid / 2 <= n) l = mid;
else r = mid - 1;
}
if (l * (l + 1) / 2 == n) l--;
return l;
}
int res[N] = { 0 };
int dfs(int n)
{
if (res[n])return res[n];
int ans = 0;
int m = n;
int k = get(m);
int num = k * (k + 1) / 2;
int d = m - num;
ans += m * m;
int cnt = 0;
if (d != k + 1)
{
cnt++;
int dd = dfs(num - k + d);
ans += dd;
}
if (d != 1)
{
cnt++;
int dd = dfs(num - k - 1 + d);
ans += dd;
}
if (cnt == 2) {
int up = num - k + d - 1;
int floor = get(up);
num = floor * (floor + 1) / 2;
d = up - num;
int dd = dfs(num - floor + d);
ans -= dd;
}
return res[m] = ans;
}
signed main()
{
IO;
int t; cin >> t;
while (t--)
{
int n; cin >> n;
for (int i = 1; i <= n; i++)vis[i] = 0;
vis[n] = 1;
int ans = dfs(n);
res[n] = ans;
cout << ans << endl;
}
return 0;
}
H. Don’t Blame Me
DP
signed main()
{
IO;
const int mod = 1e9 + 7;
int t; cin >> t;
while (t--)
{
int n, k; cin >> n >> k;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++)
cin >> a[i];
vector dp(n + 1, vector<int>(100));
int ans = 0;
for(int i = 1; i <= n; i++) {
dp[i][a[i]] = 1;
for(int j = 0; j <= 64; j++) {
dp[i][j] = (dp[i][j] + dp[i - 1][j]) % mod;
dp[i][j & a[i]] = (dp[i][j & a[i]] + dp[i - 1][j]) % mod;
}
}
for(int i = 0;i < 64;i ++){
int d = 0;
for(int j = 0;j <= 5;j ++)
if(i & (1 << j)) d ++;
if(d == k)ans = (ans + dp[n][i]) % mod;
}
cout << ans % mod << endl;
}
return 0;
}