客户生命周期可分为四个阶段:
潜在客户阶段
、
响应客户阶段
、
既得客户阶段
、
流失客户阶段
本章整体是一个客户价值预测的案例,背景是
某信用卡公司
在地推活动之后,获取了大量客户的信用卡申请信息,其中一个部分客户顺利开卡,并且有月消费记录,而另外一部分客户没有激活信用卡。公司的营销部门希望对潜在消费能力高的客户进行激活卡普的影响活动。在营销活动之前,需要对客户的潜在价值进行预测,或分析不同客户特征对客户价值的影响程度,这就涉及数值预测的相关方法,比较常用的就是
线性回归模型
1. 线性回归
线性回归中,变量分为预测变量与反应变量。对于
线性回归,自变量与因变量都是连续变量
,而在方差分析与卡方分析中,
方差分析中自变量为分类变量,因变量为连续变量
,
卡方分析中自变量与因变量都是分类变量
1.1 简单线性回归
(1) 简单线性回归原理
简单线性回归模型表达式
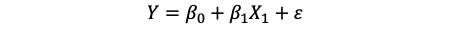
扰动项
ϵ
\color{red}{\epsilon}
ϵ
又称随机误差, 其应服从均值为0的正态分布
简单线性回归的原理就是拟合一条直线,使得实际值与预测值之差的平方和最小。当距离达到最小时,这条直线就好最好的回归拟合线
实际值与预测值之差又称残差,线性回归旨在使残差平方和最小化
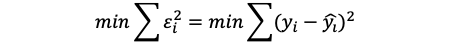
通过可解释的平方和除以总平方和得到
R
2
\color{red}R^2
R
2
, 作为线性回归拟合优度的指标;可解释的平方和指的是因为回归线带来的变异,总平方和指数据本身的变异,显然可解释的变异占总平凡和比例越大,说明模型拟合效果好;一般来说如果
R
2
\color{red}R^2
R
2
大于0.8则说明拟合效果非常好
(2) 简单线性回归检验
在简单线性回归中估计出回归系数与截距, 需要进行检验,回归系数是否为0
-
原假设:简单线性回归模型拟合得没有基线模型好,
β1
=
0
\beta_1=0
β
1
=
0
-
备择假设: 简单线性回归模型拟合得比基线模型好,
β1
≠
0
\beta_1 \neq 0
β
1
=
0
-
检验的统计量:系数估计值除以估计值的方差,服从自由度为
t−
2
t-2
t
−
2
的
tt
t
分布
t=
β
1
^
S
β
1
^
\color{blue}t=\frac{\hat{\beta_1}}{S_{\hat{\beta_1}}}
t
=
S
β
1
^
β
1
^
在多元线性回归中,还需要检验回归系数是否全部为0
-
原假设:回归系数全部都为0, 即
β1
=
β
2
=
β
3
=
⋯
=
0
\beta_1=\beta_2=\beta_3=\dots=0
β
1
=
β
2
=
β
3
=
⋯
=
0
- 备择假设: 回归系数不都为0
-
检验的统计量:
MS
M
MS_M
M
S
M
表示可解释的变异,
MS
E
MS_E
M
S
E
表示不可解释的变异
F=
M
S
M
M
S
E
\color{blue}F=\frac{MS_M}{MS_E}
F
=
M
S
E
M
S
M
1.2 多元线性回归
多元线性回归,也要求自变量与因变量之间有线性关系,且自变量之间的相关关系要尽可能的低
多元线性回归中,会涉及多个自变量,方程中的因变量线性相关性的自变量越多,回国的解释力度越强;若方程中非线性相关的自变量越多,那么模型解释力度就越弱
可以使用
R
2
R^2
R
2
评价模型解释力度,但
R
2
R^2
R
2
容易受自变量个数与观测个数的影响,在多元线性回归中,还会使用调整后的
R
2
R^2
R
2
去评价回归的优劣程度
R
‾
2
=
1
−
(
n
−
i
)
(
1
−
R
2
)
n
−
p
\color{blue}\overline{R}^2=1-\frac{(n-i)(1-R^2)}{n-p}
R
2
=
1
−
n
−
p
(
n
−
i
)
(
1
−
R
2
)
-
当有截距项时,
ii
i
等于1,反之等于0 -
nn
n
为用于拟合该模型的观察值数量 -
pp
p
为模型中参数的个数
调整后的
R
2
R^2
R
2
加入了观测个数与模型自变量个数以调整原来的
R
2
R^2
R
2
,但需要注意的是,在模型观察与自变量个数不变的情况下,评价模型解释力度的依旧是
R
2
R^2
R
2
; 在回归加入或去除某自变量后观察模型解释力度时,就要使用调整后的
R
2
R^2
R
2
1.3 多元线性回归的变量筛选
进入或剔除变量的一个准则为
AIC(Akaike Information Criterion, 赤池信息量)准则
,即
最小信息准则
,AIC值越小说明模型效果越好,越简洁
A
I
C
=
2
p
+
n
(
l
o
g
(
R
S
S
n
)
)
\color{blue}AIC=2p+n(log(\frac{RSS}{n}))
A
I
C
=
2
p
+
n
(
l
o
g
(
n
R
S
S
)
)
其中,
p
p
p
表示进入回归模型的自变量的个数,
n
n
n
为观测数量,
R
S
S
RSS
R
S
S
为残差平方和,即
∑
i
=
1
n
(
y
i
^
−
y
i
)
2
\sum_{i=1}^n(\hat{y_i}-y_i)^2
∑
i
=
1
n
(
y
i
^
−
y
i
)
2
(1) 向前回归法
-
首先将第一个变量代入回归方程,并进行
FF
F
检验和
tt
t
检验,计算残差平方和,记为
S1
S_1
S
1
-
如果通过检验,则保留该变量。然后引入第二个变量,重新构建一个新的估计方程,进行检验和
tt
t
检验,并计算残差平方和,记为
S2
S_2
S
2
-
从直观上看,増加一个新的变量后,回归平方和应该增大,残差平方和应该相应少,
S2
S2
S
2
小于等于
S1
S_1
S
1
,即
S1
−
S
2
S_1-S_2
S
1
−
S
2
的值是第二个变量的偏回归平方和,如果该值明显偏大,那么说明第二个变量对因变量有显著影响,反之则没有显著影响
(2) 向后回归法
-
该回归方式同向前回归法正好相反。首先,将所有的 X 变量一次性放入模型进行
FF
F
检验和
tt
t
检验,然后根据变量偏回归平方和的大小逐个删除不显著的变量 - 如果偏回归平方和很大则保留,反之则删除
- 向后回归法需要满足样本量大于变量个数的条件,向前回归法则无
(3) 逐步回归法
- 将变量一个一个放人方程,在引人变量时需要利明模用偏回归平方和进行检验,当显著时才加入该变量
- 当方程加该变量后,又要对原有的变量重新用偏回归平方和进行检验,一旦某变量变得不显著时便删除该変量
- 如此下去,直到老变量均不可删除,新变量也无法加为止
2. 线性回归诊断
(1) 自变量与因变量之间要有线性关系
(2) 正交假定:误差/残差与自变量不相关,其期望为0
(3) 扰动项或残差之间相互独立且服从方差相等的同一正态分布
- 残差是一种随机误差,如果其不独立说明误差不随机,依旧会有重要的信息蕴含在其中未被提取出,
- 残差同分布的意义也在于每一个残差都应出自同一正态分布
- 残差方差要尽可能相等,残差的方差与自变量相关,即存在异方差现象
2.1 残差分析
(1) 残差应服从的前提条件
- 残差不能和自变量相关(不能检验)
- 残差独立同分布
- 残差方差齐性
查看残差情况的普遍方法是查看残差图
(2) 出线残差的解决方法
-
XX
X
和
YY
Y
为非线性关系:加入
XX
X
的高阶形式,一般加
X2
X^2
X
2
-
方差不齐: 横截面数据经常表现出方差不齐现象,可以使用比如最小二乘法,稳健回归等,而最简单的方法就是对
YY
Y
取自然对数 -
自相关: 分析时间序列和空间数据时经常会遇到这个现象。复杂的方法是使用时间序列或空间计量方法进行分析;简单的方法是加入
YY
Y
的一阶滞后项进行回归
2.2 强影响点分析
在线性回归分析中,拟合的回归线会受到某个点的强烈干扰,从而改变回归线的位置,这类会对模型产生较大影响的点称为强影响点
比较常用的判断标准
- Cook’s D 统计量
- DFFITS 统计量
- DEVETAS 统计量
在数据量较大时候,可以综合考虑多个判断指标来确定强影响点
- 查看强影响点本事,确定强影响点是否存在错误
- 如果数据本事没有问题,则讲强影响点删除,再进行分析
2.3 多重共线性分析
自变量之间不能有强共线性,又称多重共线性;如果多元线性回归中存在这一问题,那么就会造成对回归系数,截距系数的估计非常不稳定
有多种方法来解决多重共线性对线性回归的影响,比如方差膨胀因子,特征根与条件指数,无截距的多重共线性分析等
方差膨胀因子
的计算公式为
V
I
F
i
=
1
1
−
R
i
2
\color{blue}VIF_i=\frac{1}{1-R^2_i}
V
I
F
i
=
1
−
R
i
2
1
其中,
V
I
F
i
VIF_i
V
I
F
i
表示自变量
X
i
X_i
X
i
的方差膨胀系数,
R
i
R_i
R
i
表示把自变量
X
i
X_i
X
i
作为因变量,与其他自变量做回归时的
R
2
R^2
R
2
显然如果自变量
X
i
X_i
X
i
与其他自变量的共线性较强,那么回归方程的
R
2
R^2
R
2
就会比较高,从而导致该自变量的方差膨胀系数比较高。一般认为,当防长膨胀因子
V
I
F
i
VIF_i
V
I
F
i
大于10时,说明有严重的多重共线性
需注意的是,无论是方差膨胀因子、特征根与条件指数还是无截距的多重共线性分析等方法,都只能有限度地减轻共线性对模型的干扰,而不能完全消除多重共线性。在处理多重共线性问题时,还有以下几种思路可供选择
-
提前筛选变量
,在回归之前通过相关检验或变量聚类的方法事先解决与变量高度相关的问题。需要注意的是,决策树和随机森林是变量重要性筛选的常用办法,但不一定能解决多重共线性,如果两个共线性的变量和因变量都很相关,那么使用决策树和随机森林分析法进行分析这两个变量都会排在前面。意 -
子集选择
是一种传统方法,其中包括逐步回归和最优子集法等,该方法通过对可能的部分子集合线性型,然后利用判别准则(如 AC 准则、BC 准则、C 准则、调整等)决定最优的模型。因为该方法是贪梦算法,在理论上这种方法只是在大部分情况下起效,在实际操作中需要与方法 1 相结合。回,こ:不品 -
收方法(shrinkage method
),收缩方法又称为正则化(regularization),主要包括岭回归(ridge regression)和 LASSO 回归。该方法通过对最小二乘估计加入惩罚约束,使某些系数的估计为 0。其中 LASSO 回归可以实现筛选变量的功能。 -
维数缩减
,包括主成分回归(PCR)和偏最小二乘回归(PS)的方法。把 P 个预测变量投影到 m 维空间(m <P),利用投影得到的不相关的组合建立线性模型。这种方法的模型可解释性差,因此不常使用。
在不更换最小二乘线性回归模型的前提下,方法 1、2、4 是可行的,而收缩方法会涉及新的回归模型
2.4 小结线性回归诊断
建立一个合理的线性回归模型应以下遵循步骤
(1) 初始分析用于确定研究目标,收集数据;
(2) 变量选择用于找到对因变量有影响力的自变量;
(3) 证模型假定,包括以下几点
- 在模型设置时,选择何种回归方法,如何选变量,以及变量以何种形式放人模型(据理论,看散点图)
- 解释变量和扰动项不能相关(根据理论或常识判断,无法检验)
- 解释变量之间不能强线性相关(膨胀系数)
- 扰动项服从独立同分布(异方差检验,D-W检验)
- 扰动项服从正态分布(QQ检验)
(4) 建立回归模型,对其进行多重共线性与强影响点的诊断与分析,若模型出线问题则需要根据具体问题修正模型
(5) 模型的预测与解释
3. 正则化方法
3.1 岭回归
3.2 LASSO回归