A. 格雷码
通常,人们习惯将所有 n 位二进制串按照字典序排列,例如所有 2 位二进制串按字典序从小到大排列为:00,01,10,11。
格雷码(Gray Code)是一种特殊的 n 位二进制串排列法,它要求相邻的两个二进制串间恰好有一位不同,特别地,第一个串与最后一个串也算作相邻。
所有 2 位二进制串按格雷码排列的一个例子为:00,01,11,10。
n 位格雷码不止一种,下面给出其中一种格雷码的生成算法:
- 1 位格雷码由两个 1 位二进制串组成,顺序为:0,1。
-
n+1 位格雷码的前 2
n
个二进制串,可以由依此算法生成的 n 位格雷码(总共 2
n
个 n 位二进制串)按顺序排列,再在每个串前加一个前缀 0 构成。 -
n+1 位格雷码的后 2
n
个二进制串,可以由依此算法生成的 n 位格雷码(总共 2n 个 n 位二进制串)按逆序排列,再在每个串前加一个前缀 1 构成。
综上,n+1 位格雷码,由 n 位格雷码的 2
n
个二进制串按顺序排列再加前缀 0,和按逆序排列再加前缀 1 构成,共 2
n
+1 个二进制串。
另外,对于 n 位格雷码中的 2
n
个二进制串,我们按上述算法得到的排列顺序将它们从 0 ∼ 2
n
−1 编号。
按该算法,2 位格雷码可以这样推出:
- 已知 1 位格雷码为 0,1。
- 前两个格雷码为 00,01。后两个格雷码为 11,10。合并得到 00,01,11,10,编号依次为 0 ∼ 3。
同理,3 位格雷码可以这样推出:
- 已知 2 位格雷码为:00,01,11,10。
- 前四个格雷码为:000,001,011,010。后四个格雷码为:110,111,101,100。合并得到:000,001,011,010,110,111,101,100,编号依次为 0 ∼ 7。
现在给出 n,k,请你求出按上述算法生成的 n 位格雷码中的 k 号二进制串。
输入格式
仅一行,包含两个整数 n 和 k。
输出格式
仅一行,一个 n 位二进制串表示答案。
数据范围
对于 50% 的数据:n≤10
对于 80% 的数据:k≤5×10
6
对于 95% 的数据:k≤2
63
−1
对于 100% 的数据:1≤n≤64,0≤k<2
n
输入样例1:
2 3
输出样例1
:
10
输入样例2
:
3 5
输出样例2
:
111
样例解释
对于样例1,2 位格雷码为:00,01,11,10,编号从 0 ∼ 3,因此 3 号串是 10。
对于样例2,3 位格雷码为:000,001,011,010,110,111,101,100,编号从 0 ∼ 7,因此 5 号串是 111。
AC代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef unsigned long long ULL;
string f(int n, ULL k)
{
if (!n) return "";
if (k < (1ull << n - 1)) return "0" + f(n - 1, k);
else
{
ULL t = (1ull << n) - 1;
if (n == 64) t = -1;
return "1" + f(n - 1, t - k);
}
}
int main()
{
int n;
ULL k;
cin >> n >> k;
cout << f(n, k) << endl;
return 0;
}
B. 括号树
本题中合法括号串的定义如下:
- () 是合法括号串。
- 如果 A 是合法括号串,则 (A) 是合法括号串。
- 如果 A,B 是合法括号串,则 AB 是合法括号串。
本题中子串与不同的子串的定义如下:
- 字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 l 与终止位置 r 来表示,记为 S(l,r)(1≤l≤r≤|S|,|S| 表示 S 的长度)。
- S 的两个子串视作不同当且仅当它们在 S 中的位置不同,即 l 不同或 r 不同。
一个大小为 n 的树包含 n 个结点和 n−1 条边,每条边连接两个结点,且任意两个结点间有且仅有一条简单路径互相可达。
小 Q 是一个充满好奇心的小朋友,有一天他在上学的路上碰见了一个大小为 n 的树,树上结点从 1 ∼ n 编号,1 号结点为树的根。
除 1 号结点外,每个结点有一个父亲结点,u(2≤u≤n)号结点的父亲为 fu(1≤fu<u)号结点。
小 Q 发现这个树的每个结点上恰有一个括号,可能是( 或)。
小 Q 定义 si 为:将根结点到 i 号结点的简单路径上的括号,按结点经过顺序依次排列组成的字符串。
显然 si 是个括号串,但不一定是合法括号串,因此现在小 Q 想对所有的 i (1≤i≤n) 求出,si 中有多少个互不相同的子串是合法括号串。
这个问题难倒了小 Q,他只好向你求助。
设 si 共有 ki 个不同子串是合法括号串,你只需要告诉小 Q 所有 i×ki 的异或和,即:
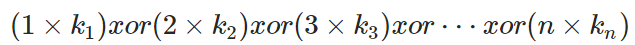
其中 xor 是位异或运算。
输入格式
第一行一个整数 n,表示树的大小。
第二行一个长为 n 的由 ( 与 ) 组成的括号串,第 i 个括号表示 i 号结点上的括号。
第三行包含 n−1 个整数,第 i(1≤i<n)个整数表示 i+1 号结点的父亲编号 fi+1。
输出格式
仅一行一个整数表示答案。
数据范围

输入样例:
5
(()()
1 1 2 2
输出样例:
6
样例解释
树的形态如下图:
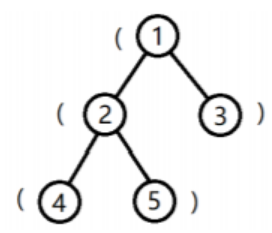
将根到 1 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 (,子串是合法括号串的个数为 0。
将根到 2 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 ((,子串是合法括号串的个数为 0。
将根到 3 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 (),子串是合法括号串的个数为 1。
将根到 4 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 (((,子串是合法括号串的个数为 0。
将根到 5 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 ((),子串是合法括号串的个数为 1。
AC代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 500010;
int n;
char str[N];
int h[N], e[N], ne[N], idx;
LL f[N], g[N];
int p[N], stk[N], top;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
if (str[u] == '(')
{
stk[ ++ top] = u;
f[u] = f[p[u]];
for (int i = h[u]; ~i; i = ne[i]) dfs(e[i]);
top -- ;
}
else
{
if (!top)
{
f[u] = f[p[u]];
for (int i = h[u]; ~i; i = ne[i]) dfs(e[i]);
}
else
{
int t = stk[top -- ];
g[u] = g[p[t]] + 1;
f[u] = f[p[u]] + g[u];
for (int i = h[u]; ~i; i = ne[i]) dfs(e[i]);
stk[ ++ top] = t;
}
}
}
int main()
{
scanf("%d", &n);
scanf("%s", str + 1);
memset(h, -1, sizeof h);
for (int i = 2; i <= n; i ++ )
{
scanf("%d", &p[i]);
add(p[i], i);
}
dfs(1);
LL res = 0;
for (int i = 1; i <= n; i ++ ) res ^= f[i] * i;
printf("%lld\n", res);
return 0;
}