博客

题目描述

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

样例描述

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4
示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1
示例 3：

输入：nums = [1], target = 0
输出：-1

思路

1. 二分查找。原本是升序的，砍掉一半放到后面
   
   
   
   因为不存在重复元素，可以肯定存在一条虚线，一个在上面一个在下面
   
   
   
   观察两段，找出第一段都满足，但是第二段不满足的
   
   
   
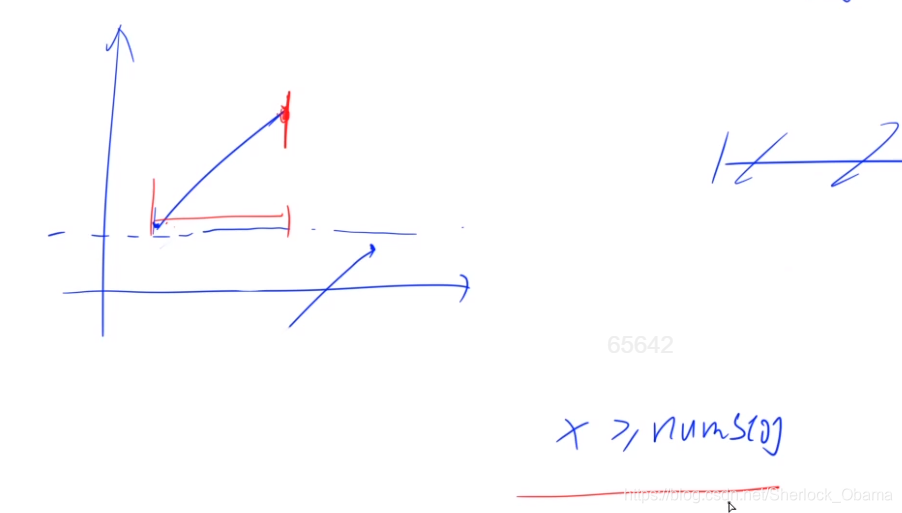
   两段的分界点就是第一段满足红线性质的最后一个数
   
   
   
   由
   
nums[mid] >= nums[0]

   可以知道，mid可能在第一段右端点或者里面，所以答案（两段分界点）一定在mid的右边，所以l要更新成mid，这样才能mid包含在右半边。
2. 确定好分界点后，在做第二次二分。用一个性质进行二分，这里用
   
x >= target

   
   
   
   此时得用
   
r = mid

   ，因为要找的目标是target分割后面那段的第一个。
3. 确定target在第一段还是第二段，判断是否大于等于
   
nums[0]

4. 二分题总结：画图，找出能够使得线分成两段的性质，用这个性质进行二分，注意根据查找结果是在前一段的最后一个还是后一段的第一个，选取不同的二分模板。

代码

class Solution {
    public int search(int[] nums, int target) {
        if (nums.length == 0) return -1;
        int l = 0, r = nums.length - 1;
        //先二分出旋转后的两个段的分界点  根据有一段大于等于nums[0]
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (nums[mid] >= nums[0]) {
                l = mid;
            }else {
                r = mid - 1;
            }
        }
        //确定target在分界点的左边段还是右边段,更新l，准备下次二分
        if (target >= nums[0]) l = 0;
        else {
            l = r + 1;
            r = nums.length - 1;
        }
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= target) {
                r = mid;
            }else {
                l = mid + 1;
            }
        }
        //判断是否等于target，因为target可能不存在
        //这里要用r，因为l可能越界，比如第二次二分根本没进入的情况
        if (nums[r] == target) return l;
        else return -1;
    }
}