1 链式地址法
题目:已知关键字序列为:(75,33,52,41,12,88,66,27),哈希表长为10,哈希函数为:H(k)=kmod7,解决冲突用线性探测再散列法,要求构造哈希表,求出等概率下查找成功的平均查找长度。
1、首先计算该序列的hash值,对该序列的每一个值都进行hash函数计算,得到结果为:
H(k)=(5,5,3,6,5,4,3,6)
| key | 75 | 33 | 52 | 41 | 12 | 88 | 66 | 27 |
|---|---|---|---|---|---|---|---|---|
| H(key) | 5 | 5 | 3 | 6 | 5 | 4 | 3 | 6 |
2、链式地址图解:
注意:链表使用的是头插法。(jdk源码是尾插法,此文不针对jdk源码)
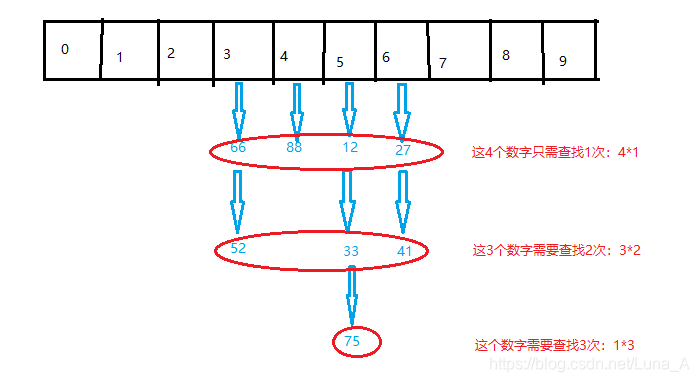
3、计算
查找成功的平均长度:(4×1+3×2+1×3)/8=13/8
查找不成功的平均长度:
第一次查找不成功:10-4=6
第二次查找不成功:10-3=7
第三次查找不成功:10-1=9
(6×1+7×2+9×3)/8=47/8
2 线性探测法
仍以上题为例。
1、hash表
| key | 75 | 33 | 52 | 41 | 12 | 88 | 66 | 27 |
|---|---|---|---|---|---|---|---|---|
| H(key) | 5 | 5 | 3 | 6 | 5 | 4 | 3 | 6 |
2、线性探测图解:
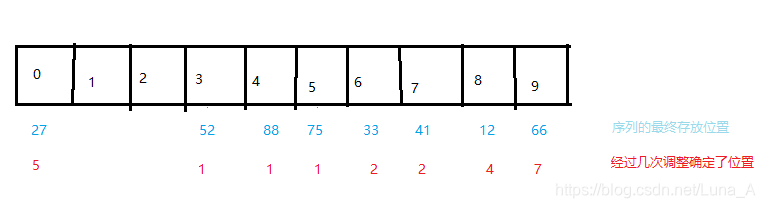
说明:
第一个key 75,它的地址是5,因此放到散列表的数组下标为5的位置,这个位置上没有关键字,因此没有冲突可以直接填入;
第二个key 33,它的地址是5,因此放到散列表的数组下标为5的位置,但这个位置上已经有关键字75,遇到了冲突,此时我们根据线性探测再散列法来处理这个冲突,探测下一个位置6, 6这个位置上没有关键字,放入即可;
第三个key 52,它的地址是3,因此放到散列表的数组下标为3的位置,这个位置上没有关键字,因此没有冲突可以直接填入;
第四个key 41,它的地址是6,因此放到散列表的数组下标为6的位置,但这个位置上已经有关键字33,遇到了冲突,此时我们根据线性探测再散列法来处理这个冲突,探测下一个位置7, 7这个位置上没有关键字,放入即可;
第五个key 12,它的地址是5,因此放到散列表的数组下标为5的位置,但这个位置上已经有关键字75,遇到了冲突,此时我们根据线性探测再散列法来处理这个冲突,探测下一个位置6, 6这个位置上已经存在关键字33,则继续增加步长1探测位置7,7上已有关键字41,探测下一个位置8,位置8上没有关键字,放入即可,到此冲突已经解决;
第六个key 88,它的地址是4,因此放到散列表的数组下标为4的位置,这个位置上没有关键字,因此没有冲突可以直接填入;
第七个key 66,它的地址是3,因此放到散列表的数组下标为3的位置,但这个位置上已经有关键字52,遇到了冲突,探测下一个位置直到发现空位置7,放入即可;
第八个key 27,它的地址是6,因此放到散列表的数组下标为6的位置,但这个位置上已经有关键字33,遇到了冲突,探测下一个位置直到发现空位置0,放入即可;
key52、88、75一次性就填入了表中,查找次数为1。
key33、41经过两次调整填入表中,查找次数为2。
key12经过四次调整填入表中,查找次数为4。
key27经过五次调整填入表中,查找次数为5。
key66经过七次调整填入表中,查找次数为7。
3、计算:
查找成功平均长度:(3×1+2×2+1×4+1×5+1×7)/8=23/8