博客

子序列：

从最初序列通过去除某些元素但不破坏余下元素的相对位置（在前或在后）而形成的新序列

子串：

将一个序列从最前或最后或同时删掉零个或几个字符构成的新系列

故子串

必是

连续的，子序列

不一定

连续


Leetcode300. 最长上升子序列

输入: [10,9,2,5,3,7,101,18]

输出: 4

解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.size()==0) return 0;
        if(nums.size()==1) return 1;

        int res=0;
        vector<int> dp(nums.size(),1);
        for(int i=0;i<nums.size();i++)
        {
            for(int j=0;j<i;j++)
            {
                if(nums[i]>nums[j])
                    dp[i]=max(dp[i],dp[j]+1);

            }
            res=max(res,dp[i]);
        }
        return res;
    }
};

最长公共子序列



Leetcode1143. 最长公共子序列


使用动态规划，最主要的就是求出其状态转移方程：

若：

input1 = [“a”, “c”, “b”, “a”, “d”],

input2 = [“a”, “b”, “c”, “a”, “d”, “f”]

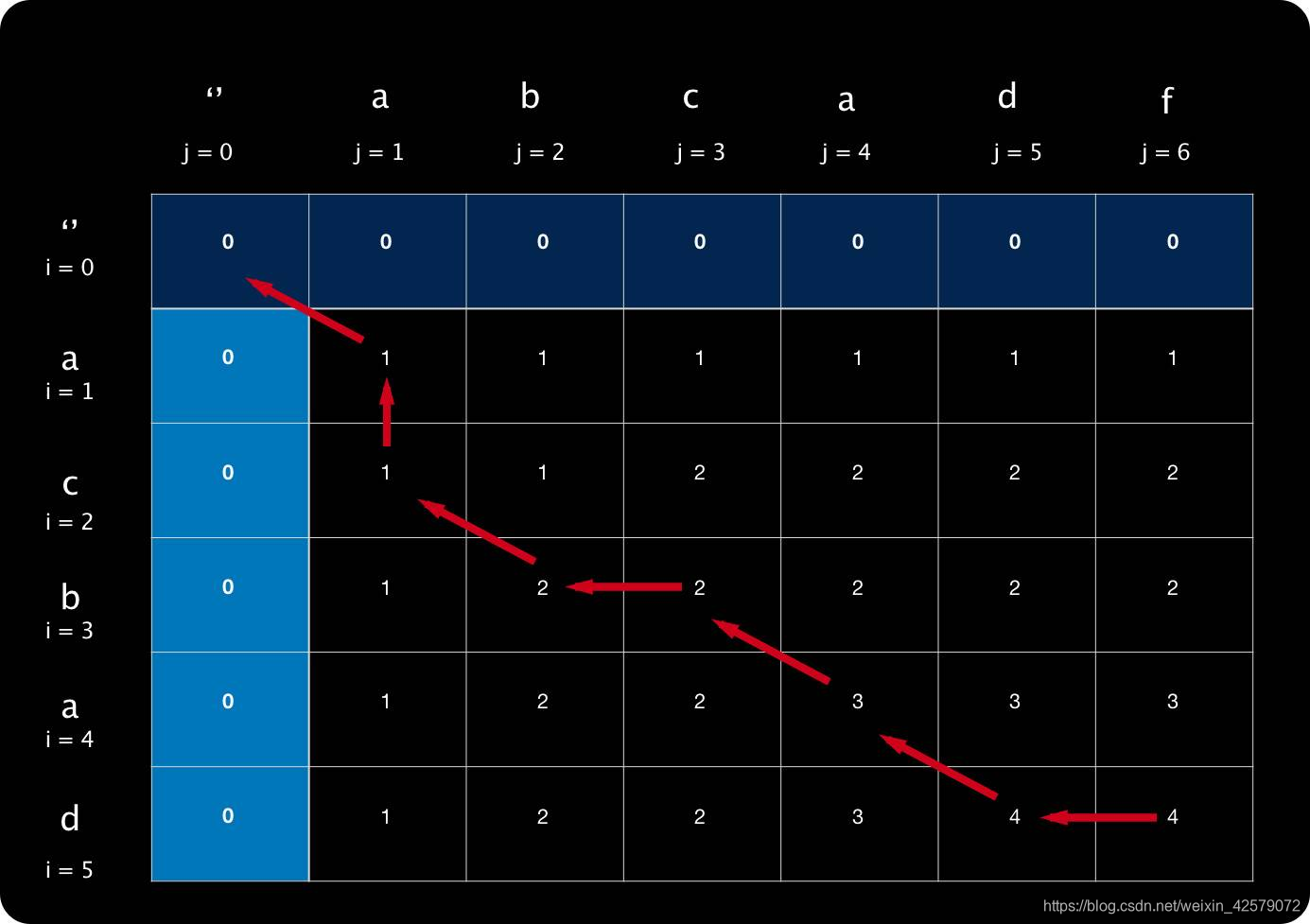
初始条件：

首先设置我们的第一个子序列为空字符串。表示字符串无法匹配，你可以理解这是一种辅助的计算方式。


状态转移方程：

当 input1[i-1] == input2[j-1]时，dp[i][j]=dp[i-1][j-1]+1。

当 input1[i-1] != input2[j-1]时，dp[i][j] = max(dp[i-1][j],dp[i][j-1])。(取它上方或左边的较大值)

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m=text1.size();
        int n=text2.size();

        vector<vector<int>> dp(m+1,vector<int>(n+1));
        //dp[0]=0;
        for(int i=1;i<m+1;i++)
        {
            for(int j=1;j<n+1;j++)
            {
                if(text1[i-1]==text2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
                else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[m][n];
    }
};

小小的扩展一下：


583. 两个字符串的删除操作


给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

输入: “sea”, “eat”

输出: 2

解释: 第一步将”sea”变为”ea”，第二步将”eat”变为”ea”

很明显就是求最长公共子序列：

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m=word1.size();
        int n=word2.size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        for(int i=1;i<m+1;i++)
        {
            for(int j=1;j<n+1;j++)
            {
                if(word1[i-1]==word2[j-1])
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return m+n-2*dp[m][n];
    }
};

最长公共子串



Leetcode718. 最长重复子数组

输入： A: [1,2,3,2,1] B: [3,2,1,4,7]

输出：3

解释： 长度最长的公共子数组是 [3, 2, 1]

若：

input1 = [“a”, “c”, “b”, “d”, “e”, “f” , “g”],

input2 = [“x”, “y”, “z”, “a”, “b”, “c”, “d”,]

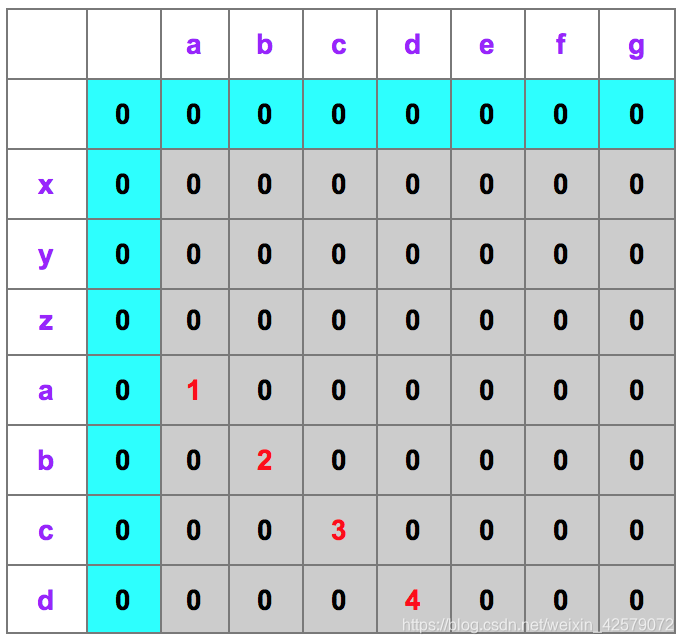
初始条件：

首先设置我们的第一个子序列为空字符串。表示字符串无法匹配，你可以理解这是一种辅助的计算方式。


状态转移方程：

当 input1[i-1] == input2[j-1]时，dp[i][j]=dp[i-1][j-1]+1。

当 input1[i-1] != input2[j-1]时，dp[i][j] = 0。

可以看出，这与最长公共子序列的区别就是第二个状态转移方程。因为子串要求是连续的，所以不等的话，只能为0；

class Solution {
public:
    int findLength(vector<int>& A, vector<int>& B) {
        int m=A.size(),n=B.size();
        vector<vector<int>> v(m+1,vector<int>(n+1,0));
        int ans=0;
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(A[i-1]==B[j-1])
                    {
                        v[i][j]=v[i-1][j-1]+1;
                        ans=max(ans,v[i][j]);
                    }
                else
                    v[i][j]=0;
            
            }
        }
        return ans;
    }
};