博客

In some scenarios/applicatons, where the precision may not be so critically important but the speed (performance) is, you may be willing to sacrifice some extent of accuracy for the speed.

In neutral networks, where the math function

where

n

is usually small (less than 2, for instance), you can avoid the expensive

exp()

provided by

math.h

(for other programming languages, similar inbuilt system functions are provided)

The

(exponential function) can be considered as the following:

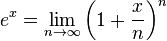
In practice,

n

cannot approach to the infinity but we can achieve a relatively good accuracy by using a large

n.

For example, if we put

, then we can multiply

by itself 8 times due to the fact

With this in mind, we can come up with the following approximation:

inline
double exp1(double x) {
  x = 1.0 + x / 256.0;
  x *= x; x *= x; x *= x; x *= x;
  x *= x; x *= x; x *= x; x *= x;
  return x;
}

We can also multiply a few more times, to increase the accuracy.

inline
double exp2(double x) {
  x = 1.0 + x / 1024;
  x *= x; x *= x; x *= x; x *= x;
  x *= x; x *= x; x *= x; x *= x;
  x *= x; x *= x;
  return x;
}

Now, you have the pattern, but for now, we need to test how accurate these approximations are:

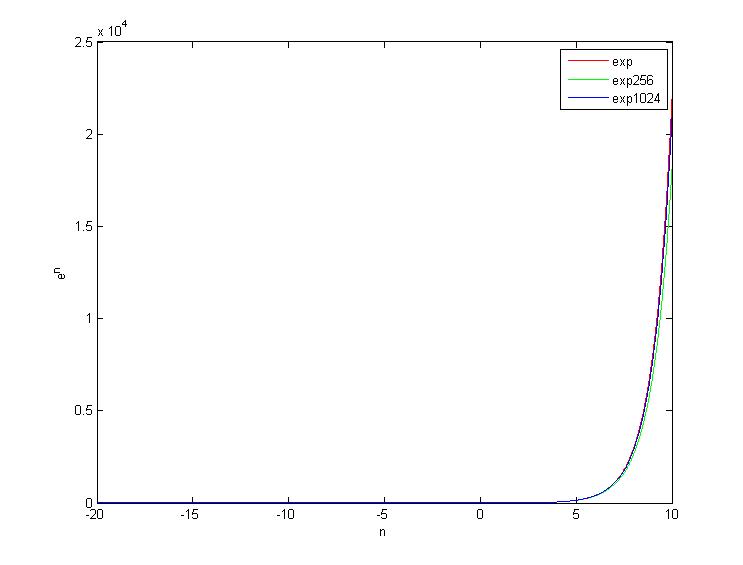
The above plots 3 curves, which are the

exp

provided by

math.h

, the

exp 256

and the

exp 1024

. They show very good agreement for input smaller than 5.

We plot the difference to make it easier to see.

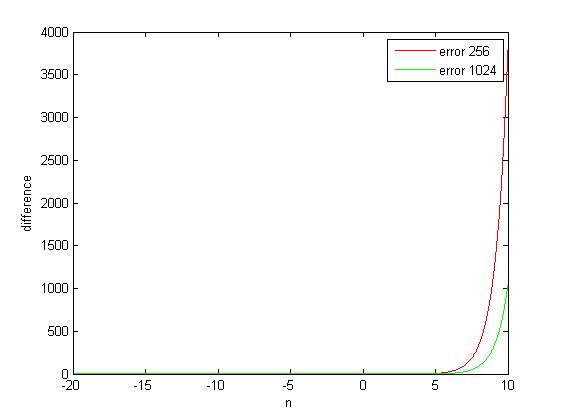
Wow, it really can be a faster alternative if the required input range smaller than 5. For negative inputs, the difference won’t be so noticeable because the value itself is so tiny that can’t be observed visually in graph.

The

exp 256

is 360 times faster than the traditional

exp

and the

exp 1024

is 330 times faster than the traditional

exp

.