题意
有
T
组测试样例,每组测试样例:
给你一棵
n
个节点的树,你要进行
n
次删除,每次删除选择树上一个没有删过的节点,将它删除,删除后会得到分数,分数等于与它连接并且没有被删除的节点个数。
例如如图所示的这样一棵树:
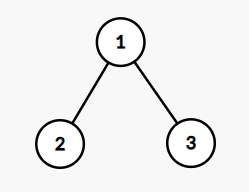
删除节点的顺序为
[2, 3, 1]
,那么分数分别是
[1, 1, 0]
,所以
[1, 2, 3]
点分别的分数就是
[0, 1, 1]
,
我们称
[0, 1, 1]
是一种分数排列
。
你可以改变删除节点的顺序,让你分别输出分数
gcd(题目规定:gcd 0 不变)= [1, n]
的分数排列有多少种情况,答案
mod 998244353
。
数据范围:
1 <= T <= 10000, 2 <= n <= 1e5, T组数据 n 的和不超过 3e5.
思路
定义
f(g)
等于
gcd = g, 2g, 3g, 4g...kg <= n
的分数排列种数的和。
我们先分别求出
f(1), f(2) ... f(n)
,然后再对其进行容斥,就能得到
gcd(1), gcd(2) ... gcd(n)
的分数排列种数。
-
对于连接
u, v
这条边,它只会影响
u, v
的分数,所以每增加一条边都会让
排列种数 * 2
,可以得到
f(
1
)
=
2
(
n
−
1
)
f(1) = 2^{(n-1)}
f
(
1
)
=
2
(
n
−
1
)
-
f(g),g = [2, n]
的分数排列种数只可能是 0 或者 1。-
我们尝试构造
g = k
的分数排列,我们从叶子节点往上进行分析。 -
对于
叶子节点
leaf
肯定不能删,因为删了就会存在分数 1,这样
gcd
就肯定不可能等于
k
了,我们只能选择删
leaf
的父亲。 -
这时候我们关注
leaf
的
父亲
f
,在不考虑
f 的父亲
的情况,删除
f
得到的分数如果不能整除
k
,那就把
f 的父亲
考虑进来,如果还是不能整除
k
,
gcd
就肯定不可能等于
k
了。如果能整除
k
,
f
和
f 的父亲
的边贡献给了谁也就知道了。 - 按照上面的思路,我们会发现分数排列只可能有一种情况。
-
我们尝试构造
-
如果
i-1
不能整除
g
,是肯定不会存在一个分数排列
gcd = g
的倍数的。
代码
#include<iostream>
#include<vector>
using namespace std;
const int N = 1e5+5;
const int MOD = 998244353;
vector<int> map_[N];
int f[N], a[N];
bool has_ans;
void dfs(int u, int f, int k) {
for(int i = 0; i < map_[u].size(); i++) {
if(!has_ans) return;
int to = map_[u][i];
if(to == f) continue;
dfs(to, u, k);
if(a[to]%k) {
a[to]++;
if(a[to]%k) has_ans = false;
} else {
a[u]++; // 当 u == 1 的时候,++ 后一定 % k == 0
}
}
}
int main(void) {
ios::sync_with_stdio(false);
int T;
cin >> T;
while(T--) {
int n;
cin >> n;
for(int i = 1; i <= n; i++) {
map_[i].clear();
f[i] = 0;
}
f[1] = 1;
for(int i = 1; i < n; i++) {
f[1] *= 2, f[1]%=MOD;
}
for(int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
map_[u].push_back(v);
map_[v].push_back(u);
}
for(int i = 2; i <= n; i++) {
if((n-1)%i != 0) continue;
for(int j = 1; j <= n; j++) a[j] = 0;
has_ans = true;
dfs(1, 0, i);
f[i] = has_ans;
}
for(int i = n; i >= 1; i--) {
for(int j = i+i; j <= n; j += i) {
f[i] = (f[i] - f[j] + MOD) % MOD;
}
}
for(int i = 1; i <= n; i++) {
cout << f[i];
if(i == n) cout << '\n';
else cout << ' ';
}
}
return 0;
}