所有节点对之间的最短路问题:给定一个加权有向图
G=(V,E)
,对于每一对结点
(
u
,
v
)
∈
V
(u,v)\in V
(
u
,
v
)
∈
V
,找到从u到v的最短路径。
-
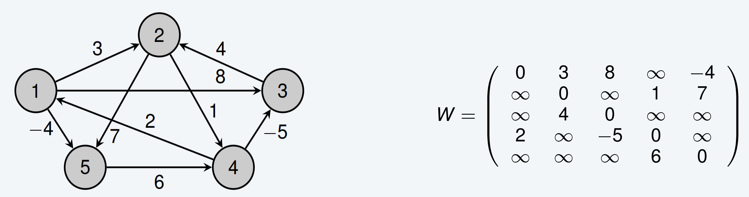
Input:用邻接矩阵表示有向加权图。
-
Output:一个n×n的矩阵
D=
(
d
i
j
)
D=(d_{ij})
D
=
(
d
i
j
)
,
di
j
d_{ij}
d
i
j
表示从i结点到j节点的最短路径。
一种简单的思路是对集合V中所有的结点使用单源最短路算法,这样就能求得所有结点之间的最短路径,时间复杂度为原时间复杂度×n(n为结点个数),但
Dijkstra
单源最短路算法不能存在负边,有向无环图的单源最短路算法不能有环,有很多限制。下面总结使用单源最短路算法的求所有节点的最短路径的算法与之后要介绍的最短路算法的限制与时间复杂度:
| Algorithm | Extra Constraints | Time Complexity |
|---|---|---|
|
Dijkastra |
“w “≥ 0 |
O ( m n log n mn\log n m n lo g n ) |
|
Bellman-Ford |
无 |
O ( m n 2 mn^2 m n 2 ) |
| Basic “matrix multiplication” | no negative weight cycle |
O ( n 4 n^4 n 4 ) |
| Improved “matrix multiplication” | no negative weight cycle |
O ( n 3 n^3 n 3 logn) |
|
Floyd-Warshall |
no negative weight cycle |
O ( n 3 n^3 n 3 ) |
一 近似矩阵乘法算法与改进
-
定义:
li
j
m
=
l_{ij}^m=
l
i
j
m
=
从
i
到
j
最多包含
m
条边的最短路径。(类似Bellman-Ford中的OPT(i,n)) -
目标:
求出所有可能顶点对(i,j)的
li
j
n
−
1
l_{ij}^{n-1}
l
i
j
n
−
1
(如果图内有负圈,最短路径一定是最多包含n-1条边的简单路径)
思考最短路问题其实包含着
最优子结构
,因此可以使用动态规划算法求解,写出
Bellman
方程:
l
i
j
m
=
{
0
i
f
m
=
0
a
n
d
i
=
j
∞
i
f
m
≠
0
a
n
d
i
=
j
m
i
n
1
≤
k
≤
n
{
l
i
k
m
−
1
+
w
k
j
}
i
f
m
>
0
l_{ij}^m=\left\{\begin{matrix} 0&if\;m=0\;and\;i=j\\ \infty& if\;m\not=0\;and\;i=j\\ \underset{1\leq k\leq n}{min}\{l_{ik}^{m-1}+w_kj\}& if\;m>0\\ \end{matrix}\right.
l
i
j
m
=
⎩
⎪
⎨
⎪
⎧
0
∞
1
≤
k
≤
n
min
{
l
i
k
m
−
1
+
w
k
j
}
i
f
m
=
0
a
n
d
i
=
j
i
f
m
=
0
a
n
d
i
=
j
i
f
m
>
0
伪代码如下:我们依次计算
L
2
,
L
3
,
.
.
.
,
L
n
−
1
L^2,L^3,…,L^{n-1}
L
2
,
L
3
,
.
.
.
,
L
n
−
1
,每次的计算过程需要分别对
i,j,k
迭代一遍。因此总的时间复杂度为
O
(
n
4
)
O(n^4)
O
(
n
4
)
算法的执行过程如图所示:
初始化一个有向加权图,
L1
L^1
L
1
就是邻接链表

迭代计算
L4
L^4
L
4

为什么说这个算法类似于矩阵的乘法呢,对比该算法与矩阵乘法,有一些相似之处:比如计算的步骤、for循环的次数以及时间复杂度都是
O
(
n
4
)
O(n^4)
O
(
n
4
)
:

改进该算法的时间复杂度,我们只对
L
i
j
m
−
1
L^{m-1}_{ij}
L
i
j
m
−
1
感兴趣,而对中间的过程不感兴趣,属于多余计算,如何能减少多余计算而又能获得结果?
-
L(
1
)
=
W
(
邻
接
矩
阵
)
L^{(1)} = W(邻接矩阵)
L
(
1
)
=
W
(
邻
接
矩
阵
)
-
L(
2
)
=
W
2
=
W
⋅
W
L^{(2)} = W^2=W\cdot W
L
(
2
)
=
W
2
=
W
⋅
W
-
L(
4
)
=
W
4
=
W
2
⋅
W
2
L^{(4)} = W^4=W^2\cdot W^2
L
(
4
)
=
W
4
=
W
2
⋅
W
2
-
L(
8
)
=
W
8
=
W
4
⋅
W
4
L^{(8)} = W^8=W^4\cdot W^4
L
(
8
)
=
W
8
=
W
4
⋅
W
4
…
-
L2
l
g
(
n
−
1
)
=
W
2
l
g
(
n
−
1
)
=
W
2
l
g
(
n
−
1
)
−
1
⋅
W
2
l
g
(
n
−
1
)
−
1
L^{2^{lg(n-1)}} = W^{2^{lg(n-1)}} = W^{2^{lg(n-1)}-1} \cdot W^{2^{lg(n-1)}-1}
L
2
l
g
(
n
−
1
)
=
W
2
l
g
(
n
−
1
)
=
W
2
l
g
(
n
−
1
)
−
1
⋅
W
2
l
g
(
n
−
1
)
−
1
因此我们只用
ceil(lg(n-1))
步就可以计算出
L
n
−
1
L^{n-1}
L
n
−
1
,总的时间复杂度缩短到
O
(
n
3
lg
n
)
O(n^3\lg n)
O
(
n
3
l
g
n
)

二 Floyd-Warshall算法
Floyd-Warshall
算法考虑的最短路径的描述与上一节中的
l
i
j
m
l_{ij}^m
l
i
j
m
有所不同,
Floyd-Warshall
算法考虑的是一条最短路径上的
中间结点
(除去起始结点与终止结点以外的结点)。
假定图G的所有结点
V
=
{
1
,
2
,
.
.
.
,
n
}
V=\{1,2,…,n\}
V
=
{
1
,
2
,
.
.
.
,
n
}
,考虑其中一个子集
V
1
=
{
1
,
2
,
.
.
.
,
k
}
V_1=\{1,2,…,k\}
V
1
=
{
1
,
2
,
.
.
.
,
k
}
,定义
d
i
j
k
d_{ij}^k
d
i
j
k
表示从
i
到
j
的最短路径的中间结点都取自{1,2,…,k}的权值。
假设从
i
到
j
的最短路径
p
的中间结点都取自
V
1
V_1
V
1
点集,
Floyd-Warshall
算法利用
p
与从
i
到
j
的最短路径的中间结点都取自
V
1
−
k
V_1-k
V
1
−
k
的关系。具体来说根据
k
是否出现在最短路径上分为:
-
结点
k
不是
p
上的中间结点,
p
上的中间结点也都属于
V1
−
k
V_1-k
V
1
−
k
,因此
di
j
k
=
d
i
j
k
−
1
d_{ij}^k=d_{ij}^{k-1}
d
i
j
k
=
d
i
j
k
−
1
-
结点
k
是
p
上的中间结点,则可以将最短路径分为
i->k->j
,每一条最短路径的中间结点都属于
V1
−
k
V_1-k
V
1
−
k
,因此
di
j
k
=
d
i
k
k
−
1
+
d
k
j
k
−
1
d_{ij}^k=d_{ik}^{k-1}+d_{kj}^{k-1}
d
i
j
k
=
d
i
k
k
−
1
+
d
k
j
k
−
1

因此我们可以写出
Bellman
方程:
d
i
j
k
=
{
w
i
j
i
f
k
=
0
m
i
n
{
d
i
j
k
−
1
,
d
i
k
k
−
1
+
d
k
j
k
−
1
}
i
f
k
>
0
d_{ij}^k=\left\{\begin{matrix} w_{ij}&if\;k=0\\ {min}\{d_{ij}^{k-1},d_{ik}^{k-1}+d_{kj}^{k-1}\}& if\;k>0\\ \end{matrix}\right.
d
i
j
k
=
{
w
i
j
m
i
n
{
d
i
j
k
−
1
,
d
i
k
k
−
1
+
d
k
j
k
−
1
}
i
f
k
=
0
i
f
k
>
0
因此算法伪代码如下:

Floyd-Warshall
算法的运行时间由三层嵌套的for循环决定,每次循环执行时间为
O
(
1
)
O(1)
O
(
1
)
,总的运行时间为
O
(
n
3
)
O(n^3)
O
(
n
3
)
。c++实现如下:
//
// Created by HP on 2021/12/1.
//
#include <iostream>
#include <cstring>
using namespace std;
#define INF 1000000000;
int V,E;
int Dis[100][100];
int Graph[100][100];
void Floyd_WarShall(){
//L0 = W 初始化为邻接矩阵
for(int i=1;i<=V;i++)
for(int j=1;j<=V;j++)
Dis[i][j] = Graph[i][j];
for(int k=1;k<=V;k++){
for(int i=1;i<=V;i++){
for(int j=1;j<=V;j++) {
//Dis[i][j] = min{Dis[i][j],Dis[i][k]+Dis[k][j]}
if(Dis[i][j] > Dis[i][k]+Dis[k][j])
Dis[i][j] = Dis[i][k]+Dis[k][j];
}
}
}
}
int main(){
cout<<"V E?"<<endl;
cin>>V>>E;
for(int i=1;i<=V;i++){
for(int j=1;j<=V;j++) {
if (i != j)
Graph[i][j] = Dis[i][j] = INF
else
Graph[i][j] = Dis[i][j] = 0;
}
}
for(int i=1;i<=E;i++){
int from,to,w;
cin>>from>>to>>w;
Graph[from][to] = w;
}
Floyd_WarShall();
for(int i=1;i<=V;i++){
for(int j=1;j<=V;j++) {
cout<<Dis[i][j]<<" ";
}
cout<<endl;
}
}
测试用例:

5 9
1 2 3
3 2 4
1 3 8
2 5 7
2 4 1
1 5 -4
5 4 6
4 3 -5
4 1 2
任意节点对之间的最短距离矩阵的运行结果如图:
