分类模型:
1、准确率、覆盖率(召回)、命中率、
Specificity(负例的覆盖率)
先看一个混淆矩阵:
| 实际\预测 | 1 | 0 | |
|---|---|---|---|
| 1(正例) |
a |
b(弃真) |
a+b |
| 0(负例) | c(取伪) | d | c+d |
| a+c | b+d | a+b+c+d |
准确率=正确预测的正反例数/总数 = (a+d) / a+b+c+d
覆盖率(召回) = 正确预测到的正例数/实际正例总数 = a / (a+b)
命中率 = 正确预测到的正例数/预测正例总数 = a / (a + c)
负例的覆盖率=正确预测到的负例个数/实际负例总数 = d / (c+d)
2、ROC(Receiver Operating Characteristic
)
、AUC(Area Under the ROC Curve)
上述的评估标准(准确率、召回率)也有局限之处:
举个例子:测试样本中有A类样本90个,B 类样本10个。分类器C1把所有的测试样本都分成了A类,分类器C2把A类的90个样本分对了70个,B类的10个样本分对了5个。则C1的分类精度为 90%,C2的分类精度为75%。但是,
显然C2更有用些
。
为了解决上述问题,人们从医疗分析领域引入了一种新的分类模型performance评判方法——ROC分析。
概念:
召回率TPR(True Positive Rate) =TP/(TP+FN) = a / (a+b)
取伪率FPR(False Positive Rate) = FP/(FP+TN) = c / (c+d)
ROC空间将取伪率(FPR)定义为 X 轴,召回率(TPR)定义为 Y 轴。
ROC理解:
不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的第一个指标应该会很高,但是第二个指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么第一个指标达到1,第二个指标也为1。

我们可以看出,左上角的点(TPR=1,FPR=0),为完美分类,也就是这个医生医术高明,诊断全对。
点A(TPR>FPR),医生A的判断大体是正确的。中线上的点B(TPR=FPR),也就是医生B全都是蒙的,蒙对一半,蒙错一半;下半平面的点C(TPR<FPR),这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医。
上图中每个阈值,会得到一个点。现在我们需要一个
独立于阈值的评价指标
来衡量这个医生的医术如何,也就是遍历所有的阈值,得到ROC曲线。

曲线距离左上角越近,证明分类器效果越好。
AUC理解:
虽然,用ROC curve来表示分类器的performance很直观好用。可是,人们总是希望能有一个数值来标志分类器的好坏。于是Area Under roc Curve(AUC)就出现了。
顾名思义,AUC的值就是处于ROC curve下方的那部分面积的大小。通常,AUC的值介于0.5到1.0之间,较大的AUC代表了较好的performance。
AUC的物理意义
假设分类器的输出是样本属于正类的socre(置信度),则AUC的物理意义为,任取一对(正、负)样本,正样本的score大于负样本的score的概率。
计算AUC:
第一种方法:AUC为ROC曲线下的面积,那我们直接计算面积可得。面积为一个个小的梯形面积之和。计算的精度与阈值的精度有关。
第二种方法:根据AUC的物理意义,我们计算正样本score大于负样本的score的概率。取N*M(M为正样本数,N为负样本数)个二元组,比较score,最后得到AUC。时间复杂度为O(N*M)。
第三种方法:与第二种方法相似,直接计算正样本score大于负样本的概率。我们首先把所有样本按照score排序,依次用rank表示他们,如最大score的样本,rank=n(n=N+M),其次为n-1。那么对于正样本中rank最大的样本,rank_max,有M-1个其他正样本比他score小,那么就有(rank_max-1)-(M-1)个负样本比他score小。其次为(rank_second-1)-(M-2)。最后我们得到正样本大于负样本的概率为
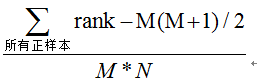
时间复杂度为O(N+M)。
对于第三种方法,这里给出例子:

对于训练集的分类,训练方法1和训练方法2分类正确率都为80%,但明显可以感觉到训练方法1要比训练方法2好。因为训练方法1中,5和6两数据分类错误,但这两个数据位于分类面附近,而训练方法2中,将10和1两个数据分类错误,但这两个数据均离分类面较远。
AUC正是衡量分类正确度的方法,将训练集中的label看两类{0,1}的分类问题,分类目标是将预测结果尽量将两者分开。将每个0和1看成一个pair关系,团中的训练集共有5*5=25个pair关系。
分别对于每个训练结果,按照第二列降序排列:
在训练方法1中,与10相关的pair关系完全正确(负样本的score都低于10的score),同样9、8、7的pair关系也完全正确,但对于6,其pair关系(6,5)关系错误,而与4、3、2、1的关系正确,故其auc为(25-1)/25=0.96;
对于训练方法2,其6、7、8、9的pair关系,均有一个错误,即(6,1)、(7,1)、(8,1)、(9,1),对于数据点10,其正任何数据点的pair关系,都错误,即(10,1)、(10,2)、(10,3)、(10,4)、(10,5),故方法2的auc为(25-4-5)/25=0.64,因而正如直观所见,分类方法1要优于分类方法2。
3、Lift
首先,给出以下名词解释:
- 正例的比例Pi1 = (a+b) / (a+b+c+d) ;
-
预测成正例的比例 Depth = (a+c) / (a+b+c+d) ;
-
正确预测到的正例数占预测正例总数的比例
PV_plus = a / (a+c) ;
-
提升值
Lift
= (a / (a+c) ) / ((a+b) / (a+b+c+d)) = PV_plus / Pi1
Lift
衡量的是,与不利用模型相比,模型的预测能力“变好”了多少。不利用模型,我们只能利用“正例的比例是 (a+b) / (a+b+c+d) ”这个样本信息来估计正例的比例(baseline model),而利用模型之后,我们不需要从整个样本中来挑选正例,只需要从我们预测为正例的那个样本的子集(
a+c
)中挑选正例,这时预测的准确率为
a / (a+c)
。
显然,lift(提升指数)越大,模型的运行效果越好。如果
a / (a+c)
就等于
(a+b) / (a+b+c+d)
(lift等于1),这个模型就没有任何“提升”了(套一句金融市场的话,它的业绩没有跑过市场)。
Reference: