初学线性代数时,对于计算矩阵幂次,是采用所谓找规律的方法,这种方法其实非常不科学。因为这样能计算的都是特别特殊的矩阵,对于一般性的矩阵,这种方法没有意义,而且所谓的找规律,只是简单的计算矩阵乘法,是命题人凑给你的。并不能看到问题的本质。
下面介绍一些一般性的方法
一.rank(A)=1 的矩阵,且能够分解为列向量乘行向量的形式。
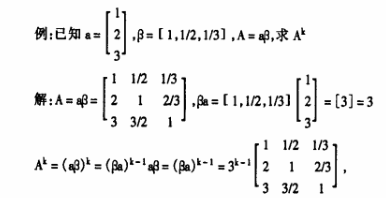
二. 可对角化的矩阵
需要对角化矩阵
三. 利用凯莱哈密顿定理分析出矩阵的性质
将矩阵幂乘转化为矩阵乘法(计算量小于对角化)
四. 利用约当标准型中零幂矩阵的性质。
任意一个方阵不一定能对角化,但总相似于约当标准型。约当标准型中的约当块满足零幂性质。

五. 对于分块矩阵
先对矩阵进行分块,在进行计算。

例题:

先分块,2*2矩阵块使用凯莱哈密顿定理

约当标准型,分解为E+A形式,二项式展开。

版权声明:本文为wwxy1995原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。