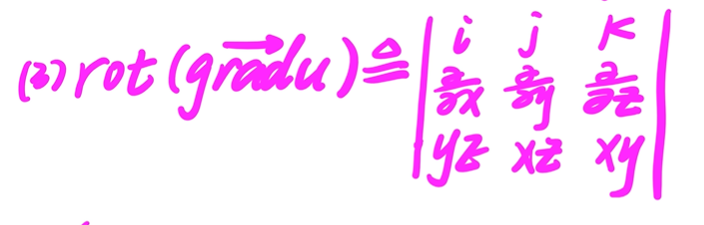文章目录
四. 多元函数微积分
二元函数的极限计算方法
- 初步判断:取 y = kx,求一元函数极限。若答案为无穷或者含k,则极限不存在。若是确定的数字,则进行第二步。
- 最终判断:取 y = kx^2 , 求一元函数极限,若答案无穷或者含k,则极限不存在。若是确定的数字,则进行下一步。
- 求值:取 y = 0.
由此可以引申出,证明重极限不存在常用方法: 取两种不同的路径,使得极限不相等或不存在。
二元函数的连续性
- 极限值 == 函数值
- 非分段 每点连续
- 分段 非分段点必连续
可偏导的定义
- 对x的偏导,就是固定y,对x的增量作差
- 可偏导的,和可导的不一样。
- 分段函数在分段点处的偏导,只能用定义求
复合函数的偏导数和全微分
对因变量 使用 求导公式,后面要 乘 偏因变量 / 偏自变量
其他自变量当成数。
方程个数 = 因变量个数
自变量 + 因变量 = 总变量
分母自变量,分子含因变量。
隐函数(抽象函数)的偏导数和全微分
考研数学中的出题需结合多种方法求解
- 方法一:基本公式
- 方法二:非单一字母,换元换成单一字母。(方法一前提)
如:z = f(x+y, v )= f(u,v)
m = f (2x , y) = f( u , y)
- 方法三:f’1 和 f’2 仍然是括号内变量的函数
对于二元函数而言
– 某点处连续与偏导毫无关系
– 对x偏导且对y偏导都存在,才可以说它偏导数存在
– 极限值 = 函数值 , 才连续
抽象函数求偏导对每一个因变量都求一次它的偏导 乘 对应自变量函数的导数
二元函数的极值和条件极值
求二元函数的极值⭐
- 求f(x,y)对x的偏导,y的偏导
- 令两个偏导 = 0 , 求驻点
- 求 对x的二阶偏导,对y的二阶偏导,对x,y的二阶偏导
- 把每个驻点代入到第三步的结果,算出A,B,C。根据AC – B^2 与 0 关系,判断是否是极值点
- 求出极值
求条件极值⭐
求 f(x,y) 在条件g(x,y)=0下的极值
∂
拉格朗日乘数法
-
确保
附加条件
一侧为0:
g(x,y)
= 0 -
构造拉格朗日函数(这里增加一个变量λ)
F(
x
,
y
,
λ
)
=
f
(
x
,
y
)
+
λ
∗
g
(
x
,
y
)
F(x,y,\textcolor{blue}λ) = f(x,y) + \textcolor{blue}λ * g(x,y)
F
(
x
,
y
,
λ
)
=
f
(
x
,
y
)
+
λ
∗
g
(
x
,
y
)
-
对每一个自变量变量求偏导,且令其值为0
{∂
F
∂
x
=
∂
f
∂
x
+
λ
∂
g
∂
x
∂
F
∂
y
=
∂
f
∂
y
+
λ
∂
g
∂
y
∂
F
∂
λ
=
λ
g
(
x
,
y
)
\begin{cases}\frac{∂F}{∂x}= \frac{∂f}{∂x} + λ\frac{∂g}{∂x} \\ \frac{∂F}{∂y}= \frac{∂f}{∂y} + λ\frac{∂g}{∂y} \\ \frac{∂F}{∂λ}= λg(x,y) \end{cases}
⎩
⎪
⎨
⎪
⎧
∂
x
∂
F
=
∂
x
∂
f
+
λ
∂
x
∂
g
∂
y
∂
F
=
∂
y
∂
f
+
λ
∂
y
∂
g
∂
λ
∂
F
=
λ
g
(
x
,
y
)
- 结合题中条件,解得极值点,代入得值。
记忆:在原本的f(x,y)上增加一个维度,条件函数作为变量。
解题技巧:对每个变量求偏导的前几个等式求关系,再代入最后一个等数
拓展:三维情况
求函数f(x,y,z)在条件g(x,y,z)=0 h(x,y,z)=0下的极值。
构造函数如下:这时候要加两个变量。
F
(
x
,
y
,
z
,
λ
,
u
)
=
f
(
x
,
y
,
z
)
+
λ
∗
g
(
x
,
y
,
z
)
+
u
∗
h
(
x
,
y
,
z
)
F(x,y,z,\textcolor{blue}λ,\textcolor{blue}u) = f(x,y,z) + \textcolor{blue}λ * g(x,y,z) + \textcolor{blue}u * h(x,y,z)
F
(
x
,
y
,
z
,
λ
,
u
)
=
f
(
x
,
y
,
z
)
+
λ
∗
g
(
x
,
y
,
z
)
+
u
∗
h
(
x
,
y
,
z
)
补充:
1. 切平面的法向量

2. 多元函数的驻点
注意:多元函数的极值点一定是驻点、但驻点不一定是多元函数的极值点。

3. 可微函数的方向导数
方向导数相当于对每一个维度的变量求偏导,得到的结果组合成一个向量。内积一个方向为l的单位向量即可。
可能结合条件极值考。

4. 平面垂直
平面垂直: 相互垂直两平面的法向量点积为 0
两平面若相互垂直, 则此两平面的法向量点积为 0
5. 方向导数、梯度、旋度
这三个的缩写要记得,不然考试考出了都不知道求什么…
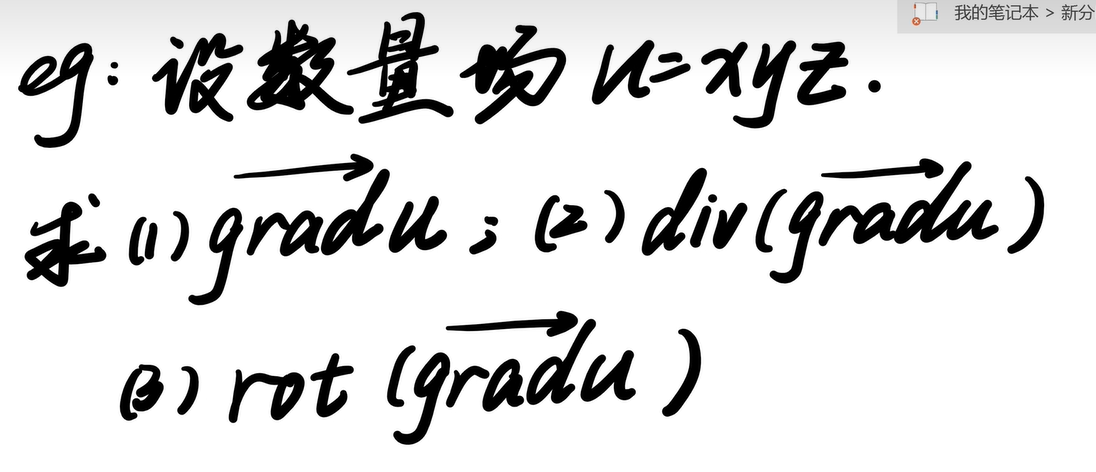
其中grad对应的是梯度, 对应一个向量表达。求解时分别对三方向下求偏导即可:
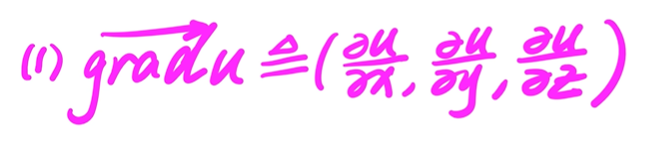
散度和旋度实际上对应的是向量的一个数值:

旋度:求解需要靠行列式计算