特别鸣谢:来自夸夸群的
醉笑陪公看落花@知乎
,
王不懂不懂@知乎
,
感谢
醉笑陪公看落花@知乎
倾囊相授,感谢小伙伴们督促学习,一起进步
关于数据结构整理非常详细的网站推荐
https://oi-wiki.org/ds/dsu/

相关文章
存在一个 无向图 ,图中有 n 个节点。其中每个节点都有一个介于 0 到 n – 1 之间的唯一编号。给你一个二维数组 graph ,其中 graph[u] 是一个节点数组,由节点 u 的邻接节点组成。形式上,对于 graph[u] 中的每个 v ,都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性:
不存在自环(graph[u] 不包含 u)。
不存在平行边(graph[u] 不包含重复值)。
如果 v 在 graph[u] 内,那么 u 也应该在 graph[v] 内(该图是无向图)
这个图可能不是连通图,也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
二分图 定义:如果能将一个图的节点集合分割成两个独立的子集 A 和 B ,并使图中的每一条边的两个节点一个来自 A 集合,一个来自 B 集合,就将这个图称为 二分图 。
如果图是二分图,返回 true ;否则,返回 false 。
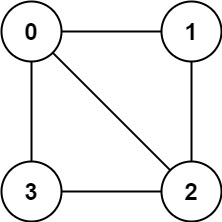
输入:graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出:false
解释:不能将节点分割成两个独立的子集,以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。
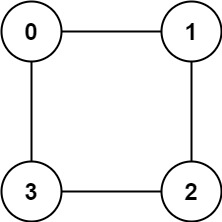
输入:graph = [[1,3],[0,2],[1,3],[0,2]]
输出:true
解释:可以将节点分成两组: {0, 2} 和 {1, 3} 。
提示:
graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n – 1
graph[u] 不会包含 u
graph[u] 的所有值 互不相同
如果 graph[u] 包含 v,那么 graph[v] 也会包含 u
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/is-graph-bipartite
方法1 穷举,设置两个集合,判断每一个节点应该放哪一个集合- 超时
时间复杂度是 O(2^n )
'''
solve 1 超时
'''
from copy import deepcopy
memor = {}
def solve1(graph):
A = set()
B = set()
return DFS(graph, A, B, 0)
count =0
def DFS(graph,A,B,i):
# print(i)
if i==37:
global count
count +=1
print(count)
if i==len(graph):return True
AA = deepcopy(A)
BB = deepcopy(B)
l=r=False
flag = True
for v in graph[i]:
if v in AA:
flag=False
break
if flag:
AA.add(i)
l = DFS(graph, AA, BB, i+1)
if l:return l
AA = deepcopy(A)
BB = deepcopy(B)
flag = True
for v in graph[i]:
if v in BB:
flag = False
break
if flag:
BB.add(i)
r = DFS(graph, AA, BB, i + 1)
return l or r
方法2 并查集 – 通过
每次把兄弟都在同一个集合中,如果发现父子放在了同一个集合,则返回false
如果所有的节点放置完毕,没有出错,则说明图可以二分
如果是多个连通分量,就设置多个集合,由于最后划分的集合未知,可以用并查集的想法。
'''
并查集
solve 2
'''
def solve2(graph):
N = len(graph)
dad = [0]*N
# init
for i in range(N):
dad[i] = i
# 合并兄弟
for u in range(N):
for v in graph[u]:
if find(dad,u) == find(dad,v):return False
union(dad,graph[u][0],v) #
return True
def find(dad,i):
if dad[i]!=i:
dad[i] = find(dad,dad[i])
return dad[i]
def union(dad,x,y):
x = find(dad,x)
y = find(dad,y)
dad[y]=x
方法3 深度优先 DFS – 通过
box = [[],[]]
def solve3(graph):
N = len(graph)
visited = [False] * N
for i in range(N): # 遍历多个子图
if visited[i]:continue
if not DFS(graph,visited,i,1):return False
return True
def DFS(graph,visited,i,lr):
if visited[i]==True: return i in box[lr]
box[lr].append(i)
visited[i]=True
for v in graph[i]:
if not DFS(graph,visited,v,1-lr):return False
return True
方法4 宽度有限遍历 BFS 层次遍历 – 通过
每次将一层的未访问过的节点加入队列,直到队列为空
每一层的结点互为兄弟,放在一个集合中,也是判断集合中是否存在父子
box = [[],[]]
def solve4(graph):
N = len(graph)
visited = [False] * N
from queue import Queue
q = Queue()
for i in range(N): # 遍历多个子图
if visited[i]:continue
lr =0
q.put([i])
while(not q.empty()):
us = q.get()
vs = []
for u in us:
if visited[u]:continue
visited[u]=True
box[lr].append(u)
for v in graph[u]:
if not visited[v]:
vs.append(v)
else:
if v in box[lr]:return False
if vs !=[]:q.put(vs)
lr = 1 -lr
return True