1. 【Part1】Contour Detection and Hierarchical Image Segmentation【轮廓检测&图像分割】

Reference from

Arbelaez, P., Maire, M., Fowlkes, C., & Malik, J. (2011). Contour detection and hierarchical image segmentation. IEEE transactions on pattern analysis and machine intelligence, 33(5), 898-916.

原文链接

https://ieeexplore.ieee.org/abstract/document/5557884

本文研究了计算机视觉中的两个基本问题：轮廓检测和图像分割。我们为这两项任务提供了最先进的算法。我们的轮廓检测器将多个局部线索组合成基于谱聚类的全局化框架。我们的分割算法包括用于将任何轮廓检测器的输出转换为分层区域树的通用机器。以这种方式，我们将图像分割的问题减少到轮廓检测的问题。广泛的实验评估表明，我们的轮廓检测和分割方法都明显优于竞争算法。可以通过用户指定的注释以交互方式细化自动生成的分层分段。多个图像分辨率的计算提供了将我们的系统耦合到识别应用程序的手段。

1. Introduction

本文提出了一种统一的轮廓检测和图像分割方法。贡献包括：

高性能轮廓检测器，结合了局部和全局图像信息，
一种在保持轮廓质量的同时将任何轮廓信号转换为区域层次的方法，
广泛的定量评估和新注释数据集的发布。

图1和图2总结了我们的主要结果。这两幅图表示使用[2]中的

精确-召回框架

，对伯克利分割数据集（BSDS300）[1]中的多轮廓检测（图1）和图像分割（图2）算法进行评估。该基准通过将机器生成的轮廓与human ground-truth数据（图3）进行比较来进行操作，并允许通过将区域边界视为轮廓来评估相同框架中的分割。

Alt
图1. Berkeley分段数据集（BSDS300）基准测试中轮廓检测器的评估[2]。领先的轮廓检测方法根据它们相对于human ground-truth 边界的最大F-度量（

⋅

精

确

率

⋅

召

回

率

精

确

率

召

回

率

\frac{2\cdot精确率\cdot召回率}{精确率+召回率}

$\frac{2 \cdot 精确率 \cdot 召回率}{精确率 + 召回率}$

）进行排序。 Iso-F曲线以绿色显示。我们的gPb检测器[3]的表现明显优于其他算法[2]，[17]，[18]，[19]，[20]，[21]，[22]，[23]，[24]，[25] 几乎在整个运作体制中，[26]，[27]，[28]。三个人(human subjects)之间的平均一致性由绿点表示。

Alt

图2. BSDS300基准测试中的分割算法评估。与我们的gPb轮廓检测器配对作为输入，我们的分层分割算法gPb -owt-ucm [4]产生的边界与其他方法产生的边界匹配ground truth的更好[7]，[29]，[30]，[31] ，[32]，[33]，[34]，[35]。

Alt

图3.伯克利分段数据集[1]。从上到下：原始图像和由三个不同的人(Human subjects)手绘的ground-truth切割边界。 BSDS300由200个训练和100个测试图像组成，每个图像具有多个ground-truth分割。 BSDS500使用BSDS300作为训练，增加了200个新的测试图像。

图1中特别值得注意的是轮廓检测器gPb，它与其他领先技术相比具有优势，为大多数召回选择提供相同或更好的精度。在图2中，gPb -owt-ucm提供了比其他分割算法更好的性能。我们分别在[3]和[4]中介绍了gPb和gPb -owt-ucm算法。本文提供了这些算法的全面版本，其设计背后的动机以及支持我们基本声明的其他实验。

我们首先回顾第2节中有关轮廓检测和图像分割的大量文献。

第3节介绍了gPb轮廓检测器的开发。我们将多尺度局部亮度，颜色和纹理线索与使用光谱聚类的强大全局框架相结合。局部线索local cues，是通过在图像中的每个位置处应用定向梯度算子计算得到的，定义了一个

亲和矩阵

，其表示像素之间的相似性。从其矩阵中，我们推导出一个通用的特征问题，并解出固定数量的特征向量，其编码了轮廓信息。使用分类器对此信号与局部线索进行重新组合，我们获得了基于相似线索构建的其他全局方案的巨大改进。

为了产生高质量的图像分割，我们将该轮廓检测器与第4节中描述的通用分组算法相关联，该算法由两个步骤组成。首先，我们引入一种称为定向分水岭变换的新图像变换，用于从定向轮廓信号构造一组初始区域。其次，使用凝聚聚类程序，我们将这些区域形成一个层次结构，该层次结构可以由超参数轮廓图表示，即通过消失的范围对每个边界进行加权而获得的实值图像。我们在BSDS300和BSDS500上提供实验，BSDS500是这里新发布的超集。

尽管

精确-召回

框架[2]已经广泛用于评估轮廓检测器，但是还需要付出相当大的努力来开发直接测量由分割算法产生的区域质量的度量。值得注意的例子包括由[5]介绍的

概率边缘指数

(Probabilistic Rand Index)，Variation of Information (shared information distance)[6]，[7]和用于PASCAL中的分割覆盖标准(Segmentation Covering criterion)[8]。我们考虑所有这些指标并证明gPb -owt-ucm提供了对现有算法的全面改进。

第5节和第6节探讨了将纯粹自下而上的轮廓和分割机制与自上而下知识的来源联系起来的方法。在第5节中，这个知识源是一个人。我们的分层区域树作为交互式分割的自然起点。使用最少的注释，用户可以纠正自动分割中的错误并从图像中拉出感兴趣的对象。在第6节中，我们针对自上而下的物体检测算法，并展示如何创建多尺度轮廓和区域输出，使其与目标检测器感兴趣的比例相匹配。

尽管要充分利用Segmentation作为中间处理层仍有许多工作要做，但最近的工作已经从这一努力中获得了回报[9]，[10]，[11]，[12]，[13]。特别是，我们的gPb -owt-ucm分割算法已用于

光流

(optical flow)[14]和物体识别[15]，[16]应用。

2. Previous Work

轮廓检测和分割的问题是相关的，但不相同。通常，

轮廓检测器不能保证它们会产生闭合轮廓，因此不一定提供将图像划分成不同区域regions

。但是它总能以边界boundary的形式从regions恢复成闭合的轮廓。作为一项成就，第4节展示了如何从轮廓检测器进行反向和恢复区域。然而，从历史上看，对这两个问题采取了不同的方法，我们现在对此进行回顾。

2.1 Contours

早期的轮廓检测方法旨在通过局部测量来量化给定图像位置处boundary的存在。

Roberts [17]，Sobel [18]和Prewitt [19]算子通过将灰度图像与局部导数滤波器(local derivative filter)进行卷积来检测边缘edge。
Marr和Hildreth [20]使用高斯算子的拉普拉斯算子的

零交叉

(Zero Crossing)。
Canny探测器[22]还将边缘模拟为亮度通道中的尖锐不连续性，增加了

非极大值抑制

(Non-Maximum Suppression)和

滞后阈值

(Hysteresis Thresholding)处理步骤。通过考虑图像对不同尺度scales和方向orientation的滤波器族的响应，可以获得更丰富的描述。一个例子是Oriented Energy方法[21]，[36]，[37]，它使用偶数和奇数对称滤波器的正交对(quadrature pairs)。
Lindeberg [38]提出了一种基于滤波器的方法，该方法具有自动尺度选择机制。

最近的局部方法考虑了颜色和纹理信息，并利用学习技术进行线索组合[2]，[26]，[27]。

Martin等人[2]定义亮度，颜色和纹理通道的梯度算子，并将它们用作逻辑回归分类器的输入，以预测边缘强度。
不依靠这样的手绘特征，Dollar 等人[27]提出了一种Boosted Edge Learning（BEL）算法，该算法试图从图像块上计算的数千个简单特征中以

概率提升树

(Probabilistic Boosting Tree)[39]的形式学习边缘分类器。这种方法的一个优点是可以在初始分类阶段处理诸如并行性和完成之类的提示。
Mairal等[26]通过学习局部图像块的

判别性稀疏表示

(discriminative sparse represnetations)来创建通用和类特定的边缘检测器。对于每个类，他们学习一个判别性字典，并使用每个字典获得的重建错误作为最终分类器的特征输入。

在图像中物体可能出现的大范围尺度仍然是这些现代局部方法的关注点。

Ren [28]将从[2]中发展出来的局部算子的多尺度中的信息结合而获益。附加定位 (additional localization)和根据多尺度检测器输出而定义的相对对比(relative contrast)线索被馈送到边界boundary分类器。对于每个比例，定位提示捕获从像素到最近的峰值响应的距离。相对对比线索根据局部邻域对每个像素进行归一化。

轮廓检测中的正交线主要关注在另一级处理，全局化，其利用局部检测器的输出。

其最简单的算法是将高梯度边缘edge片段连接在一起，以识别扩展的平滑轮廓contour[40]，[41]，[42]。
更先进的全局化阶段是以图1中基准的几种最新高性能方法的显著特征(distinguishing characterstics)，包括我们自己的方法，共享了一个共同的特征，[2]的

局部边缘检测算子

。

Ren等人[23]使用

条件随机场

（Conditional Random Fields CRF）框架来强制轮廓的曲线连续性。他们在局部检测的轮廓之上计算

受约束的Delaunay三角剖分

（constrained Delaunay triangulation CDT），从而产生由检测到的轮廓以及由三角剖分引入的新“完成”边缘组成的图。 CDT是

尺度不变

的，并且倾向于填补检测到的轮廓中的短间隙。通过将随机变量与每个轮廓和每个完成边缘相关联，它们定义了一个CRF，其具有根据探测器响应的边缘电位和根据连接类型和连续平滑度方面的顶点电位。他们使用

有环置信度传播

(Loopy Belief Propagation)[43]来计算期望。

Felzenszwalb和McAllester [25]使用不同的策略从局部轮廓检测器的输出中提取显着平滑曲线。他们考虑一组短方向线段，其连接图像中的像素到其相邻像素。每个这样的片段或是曲线的一部分或是背景片段。他们假设曲线是从马尔可夫过程（Markov process）中得出的，曲线上的

先验分布

(prior distribution)

favors few per scene

，并且在给定线段标记的情况下，检测器响应是条件独立的。找到最佳线段标记然后转换为一般加权最小覆盖问题(weighted min-cover)，其中被覆盖的元素是线段本身，并且覆盖它们的对象是从所有可能的曲线和所有可能的背景线段的集合中绘制的。由于这个问题是

NP-hard

(Non-deterministic polynoimal 非决定性多项式问题 NP)的，因此使用**“每像素成本”贪心启发式**(Greedy Heuristic)找到近似解。

Zhu等人[24]也从[2]的

输出

开始，并创建一个加权边缘图，其中权重测量相邻边缘之间的directed共线性。他们建议通过考虑归一化随机

walk matrix

的复特征向量来检测该图中的闭合拓扑循环。此过程提取闭合轮廓和平滑曲线，因为边缘链是被允许在其终止点处循环回来。

2.2 Regions

一系列广泛的分割方法涉及在局部图像块上集成亮度，颜色或纹理等特征，然后基于例如拟合混合模型

fitting mixture model

[7]，[44]，众数发现(

mode-finding

)[34]或

图划分

(Graph partitioning)[32]，[45]，[46]，[47]来聚类这些特征。由于其结合了合理的性能和公开可利用的实现，该类别中的三种算法似乎是最近应用中最广泛用作图像片段的来源。

Felzenszwalb和Huttenlocher（Felz-Hutt）[32]主张的基于图论的区域合并算法(

graph-based region merging algorithm

)试图将图像像素划分成组件component，使得得到的分割既不太粗也不太细。给定一个图，其中像素是节点并且边缘权重测量节点之间的不相似性（例如，颜色差异），每个节点最初被放置在其自己的组件中。定义组件的内部差异

(

)

Int(R)

$I n t (R)$

为

R

$R$

的

最小生成树

(Minimum Spanning Tree)中的最大权重。考虑到按权重非递减顺序的边缘，如果边缘权重小于
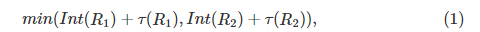
在这里插入图片描述
，

则算法的每个步骤合并由当前边缘连接的组件

R_1

$R_{1}$

和

R_2

$R_{2}$

。

其中

(

)

∣

\tau(R)=k/|R|

$τ (R) = k / ∣ R ∣$

中的

k

$k$

是一个比例参数，可用于设置组件大小的首选项。

均值漂移

(Mean Shift)算法[34]提供了一种替代的聚类框架。这里，像素表示在联合空间范围域中，通过将它们的空间坐标和颜色值连接成单个矢量。在该域中应用均值移位滤波产生每个像素的收敛点。区域region由像素组合在一起而形成，这些像素其收敛点在空间域中小于

h_s

$h_{s}$

和在范围域中小于

h_r

$h_{r}$

，其中

h_s

$h_{s}$

和

h_r

$h_{r}$

是相应的带宽参数。还可以执行附加合并(additional merging)以对最小region area实施约束。

谱图论

(Spectral Graph Theory)[48]，特别是

归一化切割准则

(Normalized Cuts criterion)[45]，[46]提供了一种将全局图像信息整合到分组grouping过程中的方法。在这个框架中，给定一个

亲和矩阵

(affinity matrix)

W

$W$

，其编码了像素之间的相似性，定义了一个对角矩阵

∑

D_{ii} =\sum_j{W_{ij}}

$D_{i i} = \sum_{j} W_{i j}$

并求解线性系统的

广义特征向量

(generalized eignvectors)：

在这里插入图片描述

传统上，在该步骤之后，应用

K均值聚类

(k-means clustering)以获得对区域的分割。这种方法经常打破均匀区域，其特征向量具有平滑梯度。一种解决方案是重新加权

亲和矩阵

[47]; 还有人提出了其他的图划分构想(Graph partitioning)[49]，[50]，[51]。

一个用于图像分割的归一化切割(Normalized Cuts)的变体是Cour等人提出的多尺度归一化切割（

Multiscale Normalized Cuts

NCuts）方法[33]。由于为了避免过于昂贵的计算而导致

W

$W$

必须是稀疏sparse的这一事实限制了其仅能使用局部像素亲和度的幼稚实现。 Cour等人解决了此限制，通过在①多个尺度上计算稀疏亲和度矩阵，②设置交叉尺度cross-scale约束以及为这种受约束的多尺度切割而推导出一个新的特征问题来。

Sharon等 [31]提出了一种提高归一化切割计算效率的替代方案。这种方法受

代数多重网格

(algebraic multi-grid)的启发，通过选择节点子集来迭代地粗化原始图形，使得精细级别上的每个变量与粗略级别上的每个变量强耦合。在[52]中采用了相同的合并策略，其中图形节点

V

$V$

的子集

S

$S$

的强耦合的形式为

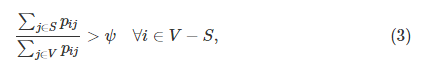
在这里插入图片描述

其中

\psi

$ψ$

是常数，

p_{ij}

$p_{i j}$

是合并

i

$i$

和

j

$j$

的概率，根据亮度和纹理相似性估算。

许多图像分割方法属于与目前为止所涵盖的类别不同的类别，依赖于variational framework中问题的表述。一个例子是Mumford和Shah [53]提出的模型，其中所观察的图像

u_0

$u_{0}$

的分割是通过公式(4)的最小化给出的：

（傅里叶变换） energy VS. power

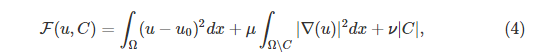
在这里插入图片描述

其中

u

$u$

在

∖

Ω∖C

$Ω ∖ C$

中是分段平滑的，

μ

$μ$

和

ν

$ν$

是加权参数。该模型的理论性质可以在例如[53]，[54]中找到。已经开发了几种算法来最小化energy(4)或其简化版本，其中

u

$u$

在

∖

Ω∖C

$Ω ∖ C$

中是分段常数。 Koepfler等人[55]为此目的提出了一种区域合并方法。 Chan和Vese [56]，[57]采用了不同的方法，在Osher和Sethian的水平集公式中表达了公式(4)[58]，[59]。 Bertelli等[30]基于成对像素相似性将此方法扩展到更一般的成本函数。最近，Pock等人[60]提出求解(4)的

凸松弛

(convex relaxation)，从而获得初始化的鲁棒性(robustness to initialization)。 Donoser等[29]将问题细分为几个图形/ground分割，每个分割使用低水平显着性 saliency 进行初始化，并通过最小化基于

总变分

(Total Variation)的energy来解决。

2.3 Benchmarks

尽管关于轮廓检测的大量文献早于其发展，但BSDS(dataset) [2]已被广泛接受作为该任务的基准(benchmark)[23]，[24]，[25]，[26]，[27]，[ 28]，[35]，[61]。评估分割算法的标准不太清楚。

一种选择是

将段边界视为轮廓

并对其进行评估。但是，也需要一种直接测量分段质量的方法。某些类型的错误（例如，两个区域之间的边界上一个丢失的像素）可能不会在边界基准boundary benchmark中反映出来，但是可能对分割质量产生实质性影响，例如，错误地合并大的区域regions。有人可能会争辩说，边界基准有利于轮廓检测器优于分割方法，因为前者不会受到要产生闭合曲线的约束的负担。因此，我们还考虑了各种based-region的指标。

2.3.1 Variation of Information (VI)

为了进行聚类比较，引入了信息变化度量[6]。它根据它们的平均条件熵(shang)来测量两个分段segmentation之间的距离

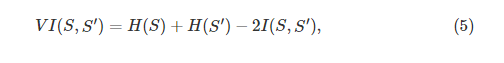
在这里插入图片描述

其中

H

$H$

和

I

$I$

分别代表熵和数据

S

$S$

和

′

S'

$S^{'}$

的两个聚类之间的共同信息。在我们的例子中，这些聚类是测试和ground-truth切割。尽管

VI

$V I$

具有一些有趣的理论性质[6]，但其在多个ground-truth分割中的感知意义和适用性仍不清楚。

2.3.2 Rand Index

最初，

兰德指数

(Rand Index)[62]被引入用于一般聚类评估。它通过比较集群clusters中元素对之间的分配兼容性(

compatibility of assignments

)来运行。在测试和ground-truth分割

S

$S$

和

G

$G$

之间的兰德指数是由在

S

$S$

和

G

$G$

中具有相同标记的像素对的数量总和以及在两个分割中具有不同标记的像素对的数量总和除以像素对的总数量。兰德指数的变体被提出[5]，[7]用于处理多个ground-truth分割的情况。给定一组ground-truth分割{

G_k

$G_{k}$

}，

概率兰德指数

(Probabilistic Rand Index)定义为

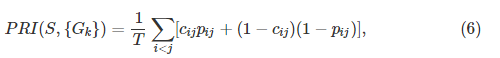
在这里插入图片描述

其中

c_{ij}

$c_{i j}$

是像素

i

$i$

和

j

$j$

具有相同标签并且其概率为

p_{ij}

$p_{i j}$

的事件，并且

T

$T$

是像素对的总数。使用

样本均值

来估计

p_{ij}

$p_{i j}$

，公式(6)相当于在不同的ground-truth分割中平均的兰德指数。

PRI

据说受到小动态范围的影响[5]，[7]，其在图像和算法上的值通常相似。在[5]中，通过对其预期值的经验估计进行归一化来解决该缺点。

2.3.3 Segmentation Covering

两个区域

R

$R$

和

′

R'

$R^{'}$

之间的

重叠

，定义为

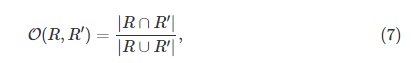
在这里插入图片描述

已被用于评估在识别中像素分类任务[8]，[11]。我们定义分段segmentation

′

S'

$S^{'}$

对分段S的

覆盖

covering

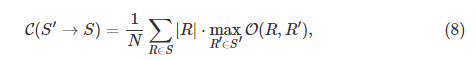
在这里插入图片描述

其中

N

$N$

表示图像中的像素总数。

类似地，ground-truth分割族{

G_i

$G_{i}$

}覆盖机器分割

S

$S$

是通过首先分别用每个人类分割

G_i

$G_{i}$

覆盖

S

$S$

(

→

G_i\rightarrow S

$G_{i} \to S$

) 然后对不同的人类分割进行平均(average {

G_i

$G_{i}$

})来定义的。为了实现完美覆盖，机器分割必须解释所有的人类数据。然后，我们可以为区域定义两个质量描述符：{

G_i

$G_{i}$

}对

S

$S$

的覆盖，和

S

$S$

对{

G_i

$G_{i}$

}的覆盖。

1. Introduction

2. Previous Work

2.1 Contours

2.2 Regions

2.3 Benchmarks

2.3.1 Variation of Information (VI)

2.3.2 Rand Index

2.3.3 Segmentation Covering

你可能也喜欢