前言:我们知道,在实数范围内,一个数和自己相乘,应该是得到一个正数;但在虚数范围内,虚数i和自己相乘得到的却是-1。该怎么理解这个结果呢?
之所以命名为虚数,在一开始的时候,没有一定的几何意义,所以数学家称其为“虚数”。直到欧拉公式的发现,虚数才有了较为清晰的认识。
欧拉公式理解虚数
在欧拉公式中,令
,得:
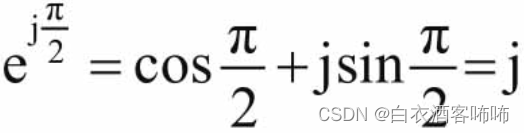
即
复数与j相乘,就是与复指数
相乘,相当于复数对应的向量逆时针旋转90°。
也就是说与复数j相乘的过程也就是,复数对应的向量旋转的过程,如图:
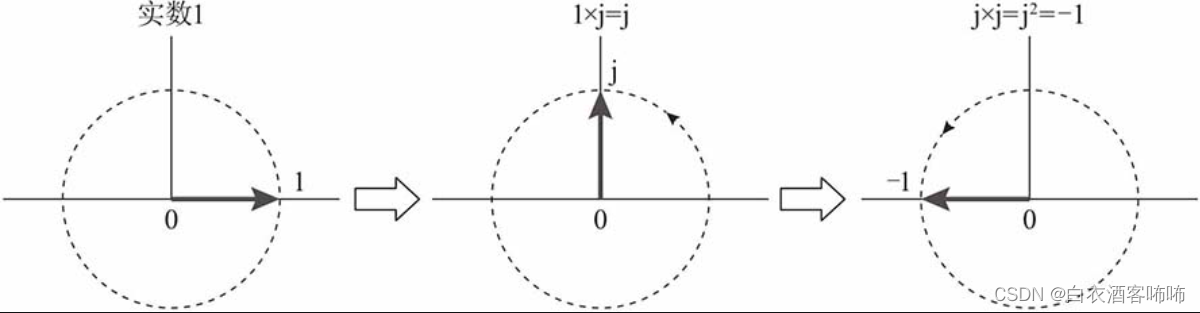
实数1对应的向量逆时针旋转90°,得到虚数j,即:1×j=j
虚数j对应的向量再逆时针旋转90°,得到实数-1,即:j×j=j2=-1
至此,我们解释清楚了为什么虚数j的平方等于-1。
版权声明:本文为hshhs1原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。